$$\color{Red}{方格取数-详细题解}$$

我做的所有的题解

包括基础提高以及一些零散刷的各种各样的题

题目说明

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

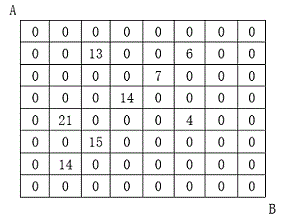
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入格式
第一行为一个整数N，表示 N×N 的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

行和列编号从 1 开始。

一行“0 0 0”表示结束。

输出格式
输出一个整数，表示两条路径上取得的最大的和。

数据范围

N≤10

输入样例：

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

输出样例：

67

二. 证明部分

正常人的第一步想法，应该是进行两次数字三角形模型的问题的结合，只不过第一次的dp需要记忆最大行走路线，然后根据第一步的路线把图像里面的点的权重清除。

但是如果记忆路线，势必要引入队列，类似走迷宫，根据可以走的四个方向进入，以此来记忆最大的那条路线，和动态规划就背道而驰，复杂度极大提高。

那么如何能保证仍然采用动态规划的同时，进行具有序列影响作用的两条路径？

我们不妨直接进入一个合并，同时走两条路径 f[i1, j1, i2, j2] 代表两条路径的终点

但是此时开销太大，四维数组，比我们最初得记忆路径还大。我们发现两条路径是同时走得，故同一时刻，两者前进得曼哈顿距离一定相等，我们设曼哈顿距离为k，为了优化空间问题，直接转化为f[k, i1, i2], 此时显然j1 = k - i1,j2 = k - i2

这只是空间优化，那么当两条路径相互影响也就是路径重叠如何解决？

很简单，两个路径每当k + 1即走了一步前，如果i1 = i2, 那么此时必然两个点重叠，只需要加一个权重值，如果不等，必然两点位置不同，需要同时加上两个点得权重。

那么具体怎么进行状态转移——》每当k+1，走到i1， i2的点，两个路径的前一状态各存在两种情况，即向下或者向右的两两组合，我们求最大值，只需要在这四种情况取最大值，加上我们上一步特判的权重，即规划完毕。

java

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    static int N = 15, n;
    static int[][] arr = new int[N][N];
    static int[][][] f = new int[2 * N][N][N];
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

    public static void main(String[] args) throws IOException {
        n = Integer.parseInt(br.readLine());
        while (true) {
            String[] str = br.readLine().split(" ");
            int a = Integer.parseInt(str[0]);
            int b = Integer.parseInt(str[1]);
            int c = Integer.parseInt(str[2]);
            if (a == 0 && b == 0 && c == 0) break;
            arr[a][b] = c;
        }
        for (int k = 2; k <= 2 * n; k++)
            for (int i1 = 1; i1 <= n; i1++)
                for (int i2 = 1; i2 <= n; i2++) {
                    int j1 = k - i1, j2 = k - i2;
                    if (j1 < 1 || j1 > n || j2 < 1 || j2 > n) continue;
                    int t = arr[i1][j1];
                    if (i1 != i2) t += arr[i2][j2];
                    f[k][i1][i2] = Math.max(Math.max(f[k - 1][i1 - 1][i2 - 1], f[k - 1][i1 - 1][i2]),
                            Math.max(f[k - 1][i1][i2 - 1], f[k - 1][i1][i2])) + t;
                }
        System.out.println(f[2*n][n][n]);
    }
}

python代码

N = 15
w = [[0]*N for i in range(N)]
f = [[[0]*N for i in range(N)] for j in range(2*N)]
n = int(input())

while 1:
    a, b, c = map(int, input().split())
    if a or b or c:
        w[a][b] = c
    else:
        break

for k in range(2, 2 * n + 1):
    for i1 in range(1, n+1):
        for i2 in range(1, n+1):

            j1, j2 = k - i1, k - i2
            if j1<1 or j1>n or j2<1 or j2>n:    continue

            t = w[i1][j1]
            if i1 != i2:
                t += w[i2][j2]

            f[k][i1][i2] = max(f[k-1][i1-1][i2-1],f[k-1][i1-1][i2],f[k-1][i1][i2-1],f[k-1][i1][i2]) + t
print(f[2*n][n][n])