AcWing 853. 有边数限制的最短路

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 853. 有边数限制的最短路原题链接简单

作者：

松鼠爱葡萄 , 2020-06-02 07:57:11 , 所有人可见 , 阅读 21589

211

152

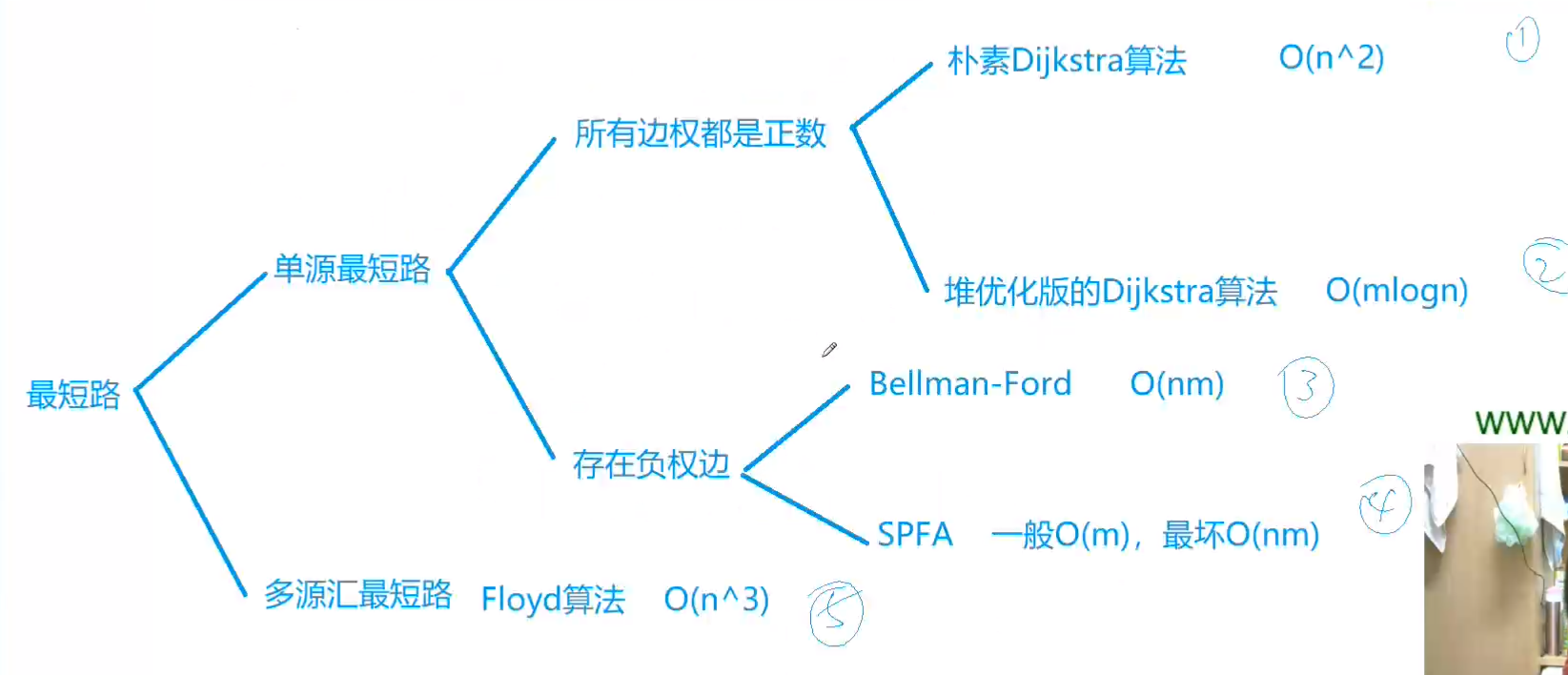
最短路.png

dijkstra 为什么不能解决解决负权边最短路问题

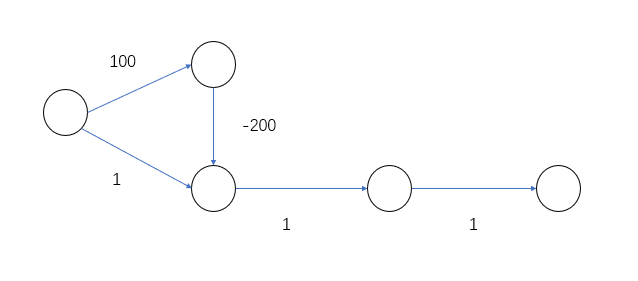
加入每条边去松弛每个点到起点的距离

dist[b] = min(dist[b], backup[a] + w);

为什么需要back[a]数组

为了避免如下的串联情况，在边数限制为一条的情况下，节点3的距离应该是3，但是由于串联情况，利用本轮更新的节点2更新了节点3的距离，所以现在节点3的距离是2。

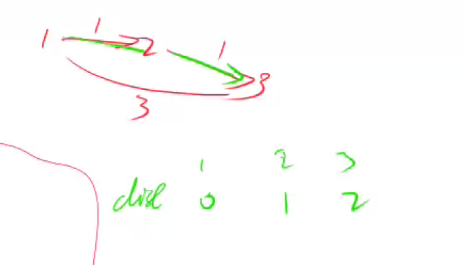
正确做法是用上轮节点2更新的距离--无穷大，来更新节点3，再取最小值，所以节点3离起点的距离是3。

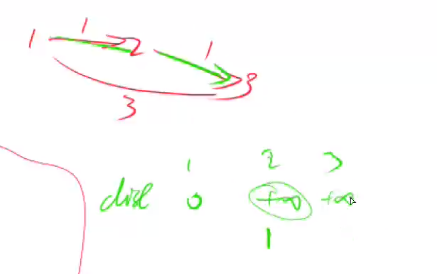
for (int i = 0; i < k; i ++ )
{
    memcpy(backup, dist, sizeof dist);
    for (int j = 0; j < m ; j ++ )
    {
        int a = edges[j].a, b = edges[j].b, w = edges[j].w;
        dist[b] = min(dist[b], backup[a] + w);
    }
}

为什么是`dist[n]>0x3f3f3f3f/2`，而不是`dist[n]>0x3f3f3f3f`

5号节点距离起点的距离是无穷大，利用5号节点更新n号节点距离起点的距离，将得到$10^9-2$, 虽然小于$10^9$, 但并不存在最短路，(在边数限制在k条的条件下)。

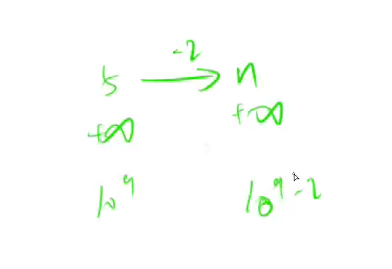
if(dist[n]>0x3f3f3f3f/2) return -1;
else return dist[n];

详细注释

#include<iostream>
#include<cstring>

using namespace std;

const int N = 510, M = 10010;

struct Edge {
    int a;
    int b;
    int w;
} e[M];//把每个边保存下来即可
int dist[N];
int back[N];//备份数组防止串联
int n, m, k;//k代表最短路径最多包涵k条边

int bellman_ford() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for (int i = 0; i < k; i++) {//k次循环
        memcpy(back, dist, sizeof dist);
        for (int j = 0; j < m; j++) {//遍历所有边
            int a = e[j].a, b = e[j].b, w = e[j].w;
            dist[b] = min(dist[b], back[a] + w);
            //使用backup:避免给a更新后立马更新b, 这样b一次性最短路径就多了两条边出来
        }
    }
    if (dist[n] > 0x3f3f3f3f / 2) return -1;
    else return dist[n];

}

int main() {
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i < m; i++) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        e[i] = {a, b, w};
    }
    int res = bellman_ford();
    if (res == -1) puts("impossible");
    else cout << res;

    return 0;
}

85 评论

dreamy 2021-02-05 15:35

边无序，上一层状态会提前改变，滚动数组即可，一样的道理

println好好学习 2022-11-25 19:10

看来同学对DP背包是有一定了解的

途_8 2023-02-22 09:18

可以看看滚动数组咋写吗，大佬；

松雅湖中学 2023-08-01 21:13

如果按正常的用树的存储方式存储，那么边就是有序的，是不是就不用备份数组了

全岛铁盒 11个月前

求一个滚动数组得写法

Pobz 2023-01-09 17:25

#include<iostream>
#include<cstring>

using namespace std;

const int N = 510, M = 10010;

struct Edge { //使用结构体存储边，不用定义一大堆数组去加边
    int a;
    int b;
    int w;
} e[M];//把每个边保存下来即可
int dist[N];
int back[N];//备份数组防止串联
int n, m, k;//k代表最短路径最多包涵k条边

void bellman_ford() {
    memset(dist, 0x3f, sizeof dist); //dist初始化位无穷，八字节3f3f3f3f大于1e9
    dist[1] = 0;
    for (int i = 0; i < k; i++) {//k次循环
        memcpy(back, dist, sizeof dist);//
        for (int j = 0; j < m; j++) {//遍历所有边，而dijkstra是遍历所有顶点n*n
            int a = e[j].a, b = e[j].b, w = e[j].w;
            dist[b] = min(dist[b], back[a] + w);
            //使用backup:避免给a更新后立马更新b, 这样b一次性最短路径就多了两条边出来
        }
    }
}

int main() {
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i < m; i++) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        e[i] = {a, b, w};
    }
    bellman_ford();
    if(dist[n]>0x3f3f3f3f/2) puts("impossible");
    else printf("%d",dist[n]);
    return 0;
}

改成这样就可以过了

阿江不会上篮 2023-10-31 19:42

强，我看的时候就想如果最短距离就是-1的时候怎么办

hfuu1 9个月前

为什么改成这样就能过？

RiL在路上 2022-11-29 21:44

amplex 2022-08-02 19:07

总算理明白各种模版的优势了，谢谢老哥

今天继续 2022-03-13 18:35

这代码现在交了怎么过不了？

acwing_1482 2022-03-26 21:54

把res==-1给改成dist[n] > 0x3f3f3f3f / 2就可

ComistryMo 2022-04-14 17:29 回复了 acwing_1482 的评论

请问为什么会这样啊

wellerency 2022-04-16 08:33 回复了 ComistryMo 的评论

如果源点到终点的距离正好是-1，那么bellman会返回-1，输出impossible。但其实正确答案是-1.

BaNg059 2022-07-30 11:14

Java把返回类型改为boolean，然后再在主函数判断一下输出impossible还是dist[n]。

println好好学习 2022-11-25 19:12 回复了 ComistryMo 的评论

可以理解为哈希碰撞，最短路径 和 用于标记无最短路径的数值 相撞

thebeatles 9个月前回复了 println好好学习的评论

哈哈哈，说的好

LДl 2022-09-01 10:14

奶斯

黎不过是个宵小 2023-04-16 19:03

哪个大佬能解释下注释里： “这样b一次性最短路径就多了两条边出来“？

黎不过是个宵小 2023-04-16 19:07

没懂这句话的意思，根本目的不就是避免更新过程中受串联影响使得目标最短距离改变成可能比正确答案更小的值而出现错误吗？？多了俩条边是什么意思呢？？

John_0 2022-07-21 12:44

歪瑞谷德

又菜了 2021-08-07 13:17

如果源点到终点的距离正好是-1，那么这个bellman_Ford会返回-1，主函数会输出impossible

六七 2021-08-16 20:30

别跟我狐闹~

又菜了 2021-08-17 11:40 回复了六七的评论

这个我已经申请加强数据了，现在这个代码过不了了

一抹暖阳 2021-08-17 13:39 回复了又菜了的评论

改成-2就AC了

又菜了 2021-08-17 14:35 回复了一抹暖阳的评论

确实，接着找yy反应反应

六七 2021-08-17 15:37

直接设置函数为void然后再函数里面判断就AC了
if(dist[n]>0x3f3f3f3f/2) puts(“impossible”);
else printf(“%d”,dist[n]);

又菜了 2021-08-17 15:47 回复了六七的评论

雀氏，这样就行

六七 2021-08-17 17:06 回复了又菜了的评论

雀氏蟀啊，我都说雀氏蟀了，你二龙啊？

又菜了 2021-08-17 18:50 回复了六七的评论

???雀食蟀

六七 2021-08-17 19:09 回复了又菜了的评论

雀食蟀=确实帅你不玩LOL的吗哈哈

又菜了 2021-08-17 19:10 回复了六七的评论

我雀氏玩

六七 2021-08-17 19:12 回复了又菜了的评论

你雀氏玩你叫狐臭你不知道zjw的吗他说的雀食蟀啊

又菜了 2021-08-17 19:14 回复了六七的评论

学习了，没时间跟你狐闹了

六七 2021-08-17 19:26 回复了又菜了的评论

别学了大佬学了一天还学

又菜了 2021-08-17 19:29 回复了六七的评论

不行啊，我啥都不会啊

Binarysearch 2021-08-19 10:34 回复了六七的评论

雀食蟀啊

天元之弈 2022-01-27 19:44

特判一下不就得了

天元之弈 2022-01-27 19:45

if(n==2&&m==1&&k==1&&a==1&&b==2&&w==-1){
puts(“-1”);
return 0;
}

在人间负债 2022-09-15 20:00

码农耕地人 2023-03-21 18:53 回复了又菜了的评论

你们两个是要笑死我啊

九折_5 5个月前

这个代码有一点小的问题，在函数中如果最后结果是无穷大，作者返回-1，刚才经过试验，数据中还真有一个就是结果是-1.哈哈哈，结果不输出-1，输出impossible。解决办法有两个一个是函数改成double，设置一个绝对不会出现的小数来判断。如下所示

if(dist[n]>0x3f3f3f3f/2) return -1.456;
    else return dist[n];

另一个是在函数外面判断就没有问题，作者的一个小漏洞吧，各位注意！

离笙i꧔ 7个月前

#include[HTML_REMOVED]
#include[HTML_REMOVED]
#include[HTML_REMOVED]

using namespace std;

const int N = 505;
const int M = 10005;

int n,m,k;
int back[N],dist[N];
struct edge
{
int a,b,w;
}e[M];

int bellman()
{
memset(dist,0x3f,sizeof dist);
dist[1] = 0;

for(int i = 1;i<=k;i++) 
{
    memcpy(back,dist,sizeof dist);
    for(int j =1;j<=m;j++) 
    {
        int a = e[j].a, b =e[j].b, w =e[j].w;
        dist[b] = min(dist[b] , back[a] + w);
    }
}

 return dist[n];

}

int main()
{
cin>>n>>m>>k;

for(int i = 1;i<=m;i++) 
{
    int a,b,w;
    cin>>a>>b>>w;
    e[i] = {a,b,w};
}

int t = bellman();
if(t > 0x3f3f3f3f /2)  cout<<"impossible"<<endl;
else cout<<t<<endl;

return 0;

}