题目描述
n个水果排成一排
有两种水果,用0和1表示
相邻的一堆同种水果被称作一个块
每次将所有块的块头取出做成一个果篮
块的消失可能导致前后两个块合并
求所有果篮中的水果
正常的链表思路
每个水果建一个点,从前往后搜
搜到和上一个不同的就从链表中删除
(图为手绘十分粗糙敬请谅解)
灰常正常的思路
但是
它有可能会被卡掉。
比如整排水果全部是一个块
每次只取出一个,但都需要遍历整排
复杂度退化为$O(n^2)$
TLE灰常开心
链表套链表思路
我们发现如果把一个块作为节点,就可以避免上述问题
(多块不大,大块不多)
合并时,
为避免一个节点内存过多信息(比如所有节点的编号)
不需要真正将两个块合并
只需要把它们用链表串起来。(将该链表命名为链表1)
因为初始创块时每个块内节点编号一定等于上一个节点+1
所以只需要存当前初始的点
取走时直接加一。
至于题目所说的那些开头元素,只需要再开一个链表(命名为链表2)
存所有并没有串到别的块后面的块的编号。
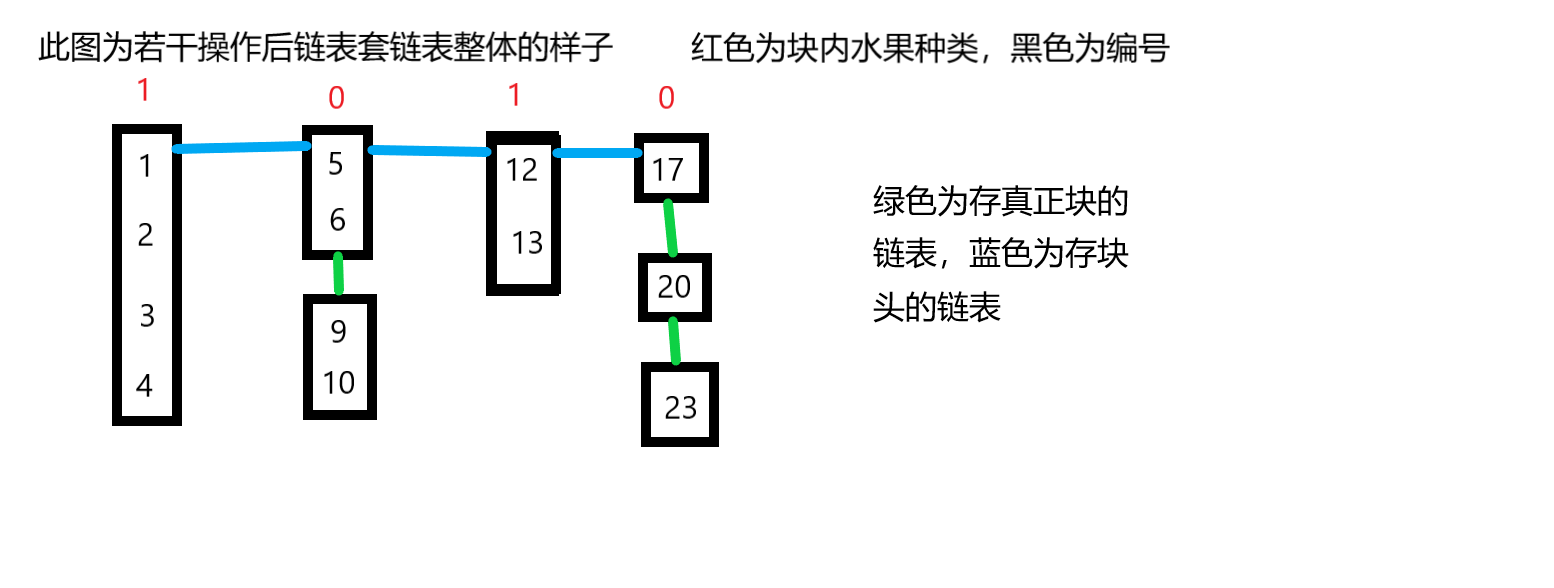
节点信息
梳理一下一个节点需要存什么信息
1.该块的颜色
2.开始位置编号
3.长度(方便判断块消失)
4.链表1中的下一个块(没有的话为0)
5.链表1中该链的结尾(只需要维护链头的该数据即可)
果篮处理
从前往后扫描链表2
扫描过程中可以顺便去除两个链表中空的那些块
如果当前扫描到的块和上一个的种类不同
就取出它的队头
如果它消失了,就顺着链表1往下找
如果上一个块还健在,这个块和上一个的种类相同
把它插到上一个块在链表1的链尾处
如果前面的条件都不满足
可以直接跳过,下次扫描再作处理。
最后我们发现链表2只会有删除中间某个节点一种操作
可以直接用队列模拟(编起来更省事)
完整代码
#include<iostream>
#include<queue>
using namespace std;
const int N=200005;
struct node{
int c,b,l; //c存块的颜色,b存开始的位置,l存长度
int ne,t; //ne存下一个待合并的块,t存最后一个待合并的块
}bs[N];
int cnt;
queue<int> que;
int main(){
int n,lastc=2;
scanf("%d",&n);
for(int i=1;i<=n;i++){
int c;
scanf("%d",&c);
if(c!=lastc){
if(i!=1)
que.push(cnt); //插入上一个块
bs[++cnt].c=c;
bs[cnt].b=i;
bs[cnt].l=1;
bs[cnt].t=cnt;
}
else
bs[cnt].l++;
}
que.push(cnt); //插入最后一个块
lastc=2;
int lastb=0; //上一个块
while(que.size()){
int x=que.front();
que.pop();
if(bs[x].c!=lastc||lastb>=x){ //是一个真正的块
if(lastb>=x) //是全排第一个块
printf("\n");
printf("%d ",bs[x].b++); //取出块头
bs[x].l--;
while(!bs[x].l&&bs[x].ne){ //空了就顺着链表1往下找
bs[bs[x].ne].t=bs[x].t;
x=bs[x].ne;
}
if(bs[x].l) //如果该块真的逝世了就可以不去管它
que.push(x);
lastb=x; //更新上一个块
lastc=bs[x].c;
}
else if(bs[lastb].l){ //插到上一个块的末尾
bs[bs[lastb].t].ne=x;
if(!bs[x].t)
bs[lastb].t=x;
else
bs[lastb].t=bs[x].t;
}
else{ //下次再做处理
que.push(x);
lastb=x;
}
}
return 0;
}

