<—点个赞吧QwQ

宣传一下算法提高课整理{:target=”_blank”}

给定一个长度为 $N$ 的数组，数组中的第 $i$ 个数字表示一个给定股票在第 $i$ 天的价格。

设计一个算法来计算你所能获取的最大利润，你最多可以完成 $k$ 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。一次买入卖出合为一笔交易。

输入格式

第一行包含整数 $N$ 和 $k$，表示数组的长度以及你可以完成的最大交易笔数。

第二行包含 $N$ 个不超过 $10000$ 的正整数，表示完整的数组。

输出格式

输出一个整数，表示最大利润。

数据范围

$1 \\le N \\le 10^5$,
$1 \\le k \\le 100$

输入样例1：

3 2
2 4 1

输出样例1：

2

输入样例2：

6 2
3 2 6 5 0 3

输出样例2：

7

样例解释

样例1：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

样例2：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。共计利润 4+3 = 7.

思路

闫氏$\text{DP}$分析法：
状态表示：$f_{i,j,k}$其中$k=0/1$

• 集合：目前是第$i$天，且已完成$j$笔完整交易，并且当前持股$(k=1)$或未持股$(k=0)$
• 属性：$\max$

状态计算：

• 如果第$i$天持有股，那么既可以由第$i-1$天持有股，也可以买入，即$f_{i,j,1}=\max\lbrace f_{i-1,j,1},f_{i-1,j,0}-a_i\rbrace$
• 如果第$i$天未持股，那么即可以由第$i-1$天未持股，也可以卖出，即$f_{i,j,0}=\max\lbrace f_{i-1,j,0},f_{i-1,j-1,1}+a_i$

答案：根据定义，最后持股的方案一定不是最优解，所以答案就是$\underset{0 \le i \le k}{\max}f_{n,i,0}$

状态机：
来自一只野生彩色铅笔

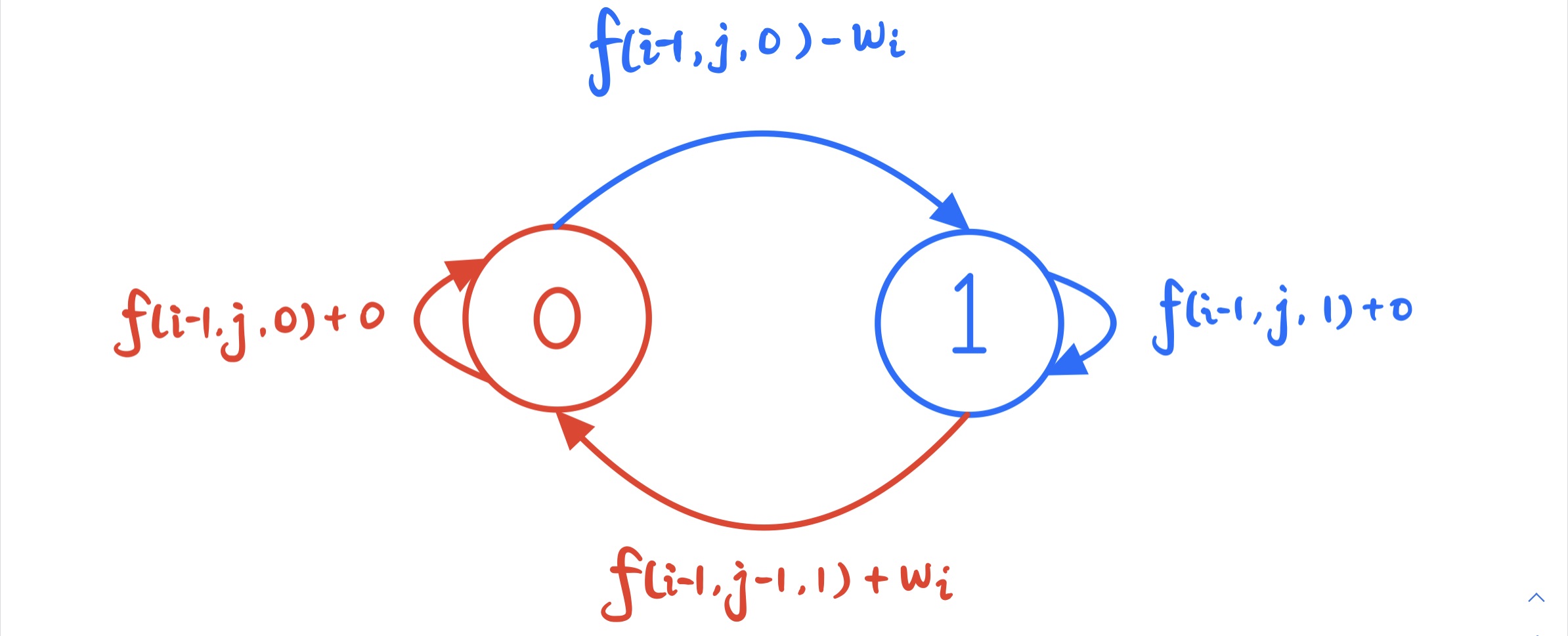
代码

#include <iostream>
#include <cstring>
using namespace std;
const int N = 100010,K = 110;
int n,k;
int a[N];
int f[N][K][2];
int main () {
    cin >> n >> k;
    for (int i = 1;i <= n;i++) cin >> a[i];
    memset (f,-0x3f,sizeof (f));
    f[0][0][0] = 0;
    for (int i = 1;i <= n;i++) {
        for (int j = 0;j <= k;j++) {
            f[i][j][0] = f[i - 1][j][0];
            if (j) f[i][j][0] = max (f[i][j][0],f[i - 1][j - 1][1] + a[i]);
            f[i][j][1] = max (f[i - 1][j][1],f[i - 1][j][0] - a[i]);
        }
    }
    int ans = 0;
    for (int i = 0;i <= k;i++) ans = max (ans,f[n][i][0]);
    cout << ans << endl;
    return 0;
}