AcWing 1064. 小国王

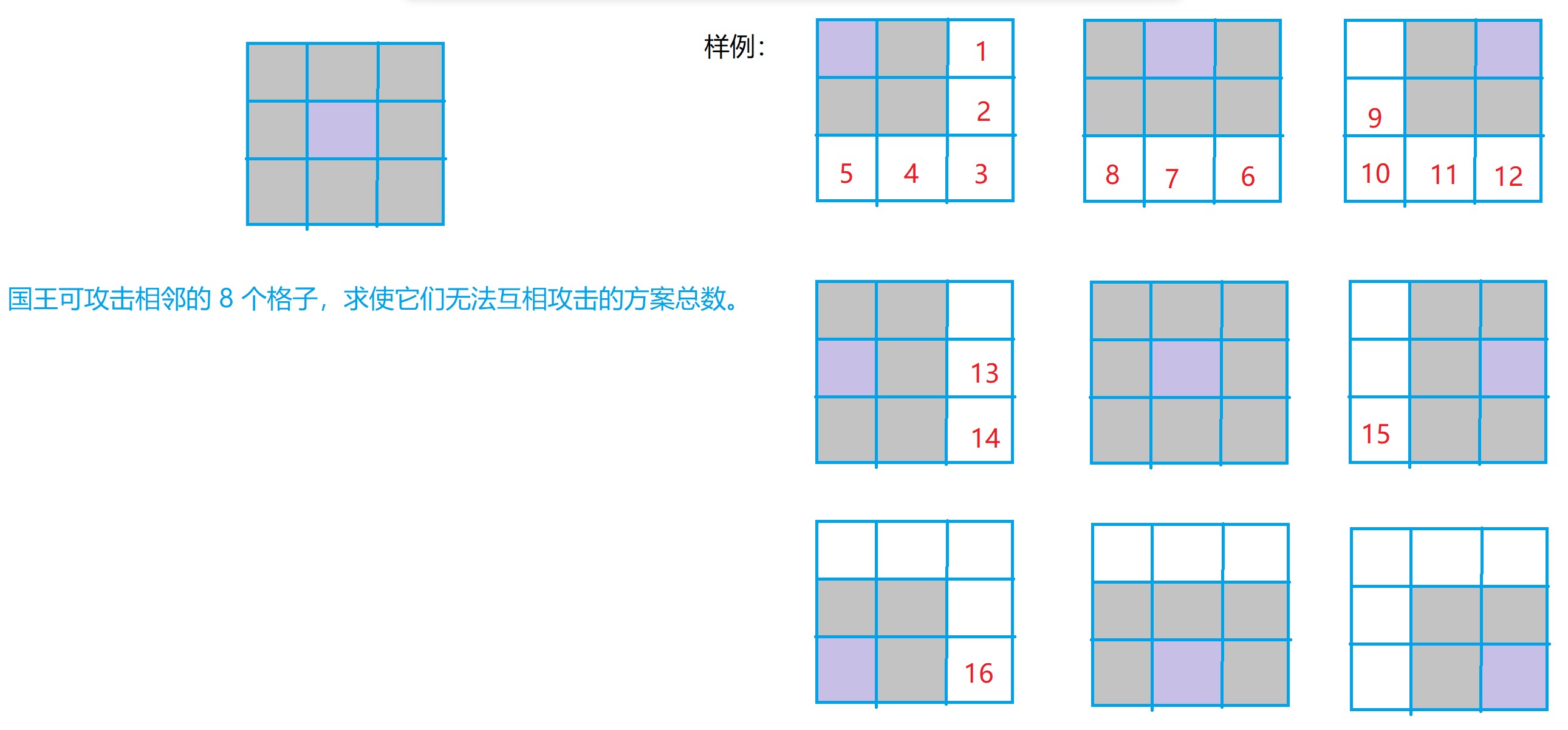
[分析]

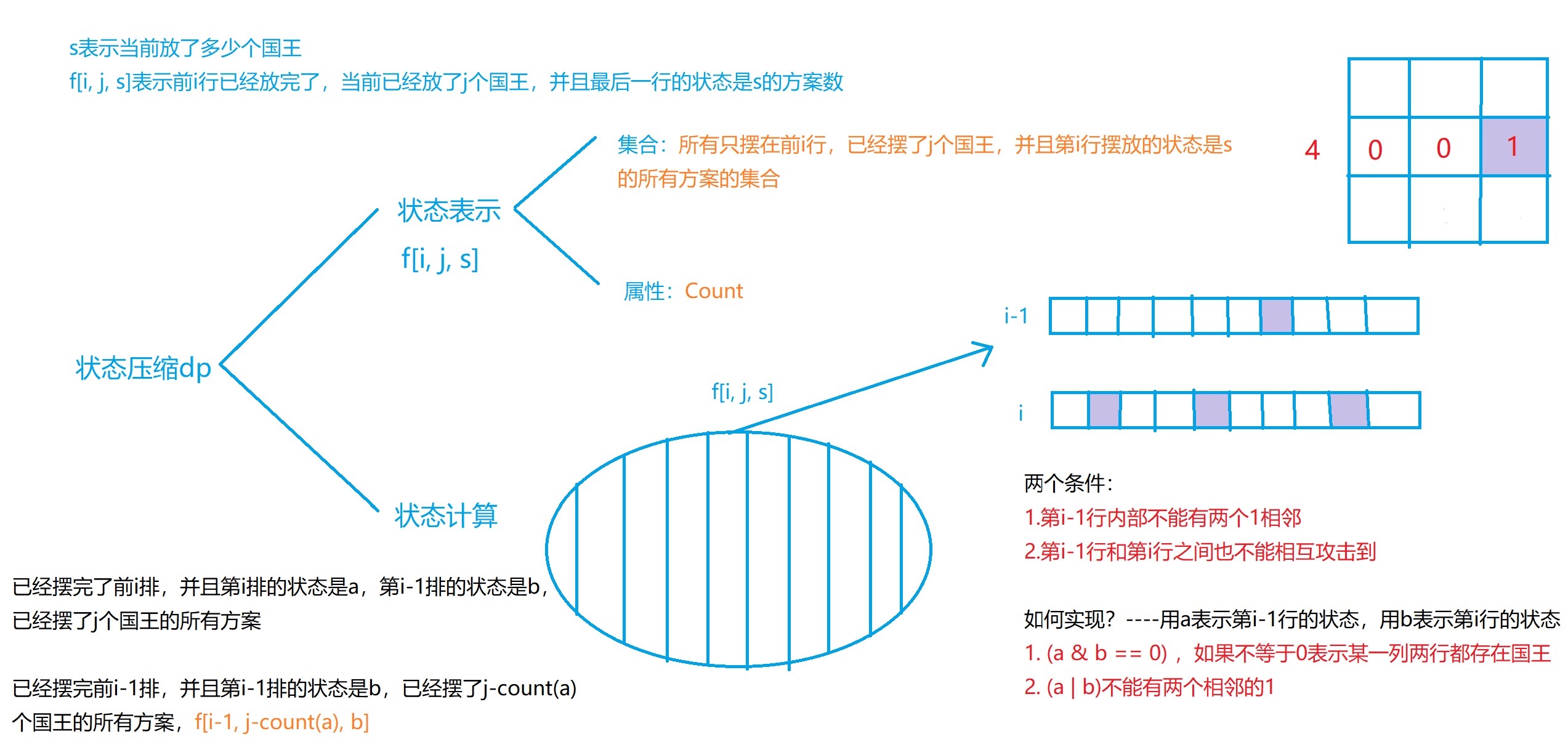
1. 状态表示$f(i, j, s)$：
   集合：所有只摆在前$i$行，已经摆了$j$个国王，并且第$i$行摆放的状态是$s$的所有方案数的集合。
   属性：Count
2. 状态计算

参考自算法提高课 y总的解法

#include<iostream>
#include<vector>
using namespace std;

const int N = 12, M = 1 << N, K = 110;

int n, m;
vector<int> state;  // 表示所有合法状态
int cnt[M]; // 每个状态1的个数
vector<int> head[M];   // 每个状态所有可以转移到的其他状态
long long f[N][K][M];

// 检查是否存在连续的两个1，不存在合法
bool check(int state)
{
    for(int i = 0; i < n; i ++ )
        if((state >> i & 1) && (state >> i + 1 & 1))
            return false;
    return true;
}

int count(int state)
{
    int res = 0;
    for(int i = 0; i < n; i ++ ) res += state >> i & 1;
    return res;

}

int main()
{
    cin >> n >> m;

    // 预处理
    for(int i = 0; i < 1 << n; i ++ )
        if(check(i))
        {
            state.push_back(i);
            cnt[i] = count(i);  // i里面1的个数
        }


    // 不同状态之间边的关系
    for(int i = 0; i < state.size(); i ++ )
        for(int j = 0; j < state.size(); j ++ )
        {
            int a = state[i], b = state[j]; // a表示第一个状态，b表示第二个状态
            // 预处理哪些状态和哪些状态之间可以转移
            if((a & b) == 0 && check(a | b))
                head[i].push_back(j);
        }

    f[0][0][0] = 1;
    for(int i = 1; i <= n + 1; i ++ )
        for(int j = 0; j <= m; j ++ )
            for(int a = 0; a < state.size(); a ++ )
                for(auto b : head[a])
                {
                    int c = cnt[state[a]];
                    if(j >= c)
                        f[i][j][a] += f[i - 1][j - c][b];
                }

    cout << f[n + 1][m][0] << endl;

    return 0;
}