题目描述

求把 $N \\times M$ 的棋盘分割成若干个 $1 \\times 2$ 的长方形，有多少种方案。

例如当 $N=2，M=4$ 时，共有 $5$ 种方案。当 $N=2，M=3$ 时，共有 $3$ 种方案。

如下图所示：

输入格式

输入包含多组测试用例。

每组测试用例占一行，包含两个整数 $N$ 和 $M$。

当输入用例 $N=0，M=0$ 时，表示输入终止，且该用例无需处理。

输出格式

每个测试用例输出一个结果，每个结果占一行。

数据范围

$1 \\le N,M \\le 11$

输入样例：

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

输出样例：

1
0
1
2
3
5
144
51205

状态压缩DP

说明

核心是一旦横着的确定，在合法放的情况下，竖着的只有一种存放的方法，所以只需要考虑横着放就可以。

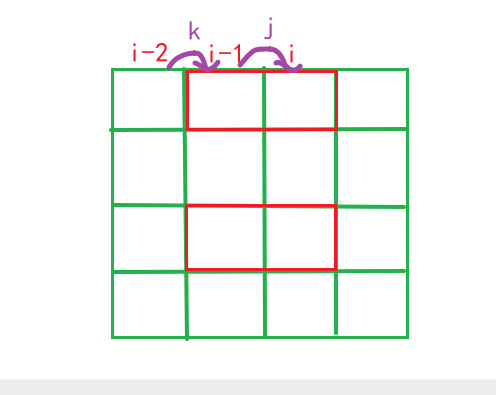
    f[i][j]: 表示第i-1伸到第i列的状态为j的合法的总方案数目
    j为二进制数，伸出为1，不伸出为0
    k为第i-2列向i-1列伸出的状态。

怎么算合法的方案呢？

1. 从 $i-2$ 伸向 $i-1$ ，和从 $i$ 伸向 $i-1$ 不能同时，不然会发生冲突。

   如果 $i$ 伸向了 $i-1$ ，那么 $i-1$ 一定也是伸向 $i$ 的，因为是一个 $1*2$ 的。一个意思。
   

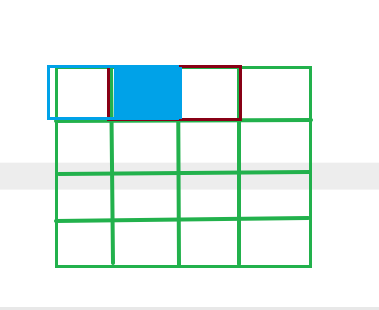
   所以 $j$ 和 $k$ 不能同时为 $1$ ，也就是 $j\&k == 0$

2. 第 $i-1$ 列连续的 $0$ 必须为偶数，否则无法存放竖着的。

var st [M]bool //记录i状态下 所有的连续空位是不是偶数
for i := 0; i < 1 << n; i ++ { //枚举每一个状态
    st[i] = true
    cnt := 0 //连续为0的一段的 0的个数
    for j := 0; j < n; j ++ {//查看每一个状态的每一位
        if i >> j & 1 == 1 { 
            //当前为1 说明连续为0的一段结束了 判断一下cnt是否为偶数
            if cnt & 1 == 1{
                st[i] = false
                break
            }
            cnt = 0
        }else{
            cnt++
        }
    }
    if cnt & 1 == 1 {//判断最后一段连续的0
        st[i] = false 
    }
}

DP过程

var f [N][M]int //表示第i-1伸到第i列的状态为j的合法的总方案数目
f[0][0] = 1
//应该从第0列开始放，所以-1列伸向0列的状态为0 是一个合法的方案，所以f[0][0]=1
for i := 1; i <= m; i ++ {//枚举每一列
    for j := 0; j < 1 << n; j ++ { //枚举第i列的状态 也就是从i-1列向i列伸出的可能状态
        for k := 0; k < 1 << n; k ++ { //枚举第i-1列的状态 也就是从i-2列向i-1列伸出的可能状态
            if j & k == 0 && st[j | k] { //j|k 可以这么理解：i-2列伸向i-1列的可能状态和i-1列伸向i的可能状态 共同作用下是对于i-1列最终向i列伸出的一个状态，
                //判断这个状态是否合法 求所有合法状态数量的累加和
                f[i][j] += f[i-1][k]
            }
        }
    }
}
fmt.Println(f[m][0])
//最后一列为m-1, 我们最终求的是从m-1列向m列伸出的状态全部为0 所以我们最后的结果是f[m][0]

这个DP过程如果判断的两个条件交换一下位置，可能会超时。下面是一个优化版本的，优化的思路就是先提前存储好某个状态 $j$ 对应的合法的 $k$ 状态。

//预处理2
var state[M][]int //某个状态j 所对应的k状态 共同作用下是一个合法的状态
for j := 0; j < 1 << n; j ++ {
    for k := 0; k < 1 << n; k ++ {
        if j & k == 0 && st[j | k] { 
            state[j] = append(state[j], k)   
        }
    }
}
var f [N][M]int
f[0][0] = 1
for i := 1; i <= m; i ++ {//枚举每一列
    for j := 0; j < 1 << n; j ++ {
        for _, k := range state[j] {
            f[i][j] += f[i-1][k] //当前状态数等于之前第i-1列所有的合法方案数
        }
    }
}
fmt.Println(f[m][0])

go代码(全部)

package main

import "fmt"

const N = 12
const M = 1 << N
func main(){
    var n, m int
    for {
        fmt.Scan(&n, &m)
        if n == 0 && m == 0 {
            break
        }
        //预处理1，某一列连续的0状态的个数必须为0
        var st [M]bool
        for i := 0; i < 1 << n; i ++ { //枚举每一个状态
            st[i] = true
            cnt := 0 //连续为0的一段的 0的个数
            for j := 0; j < n; j ++ {//查看每一个状态的每一位
                if i >> j & 1 == 1 { 
                    //当前为1 说明连续为0的一段结束了 判断一下cnt是否为偶数
                    if cnt & 1 == 1{
                        st[i] = false
                        break
                    }
                    cnt = 0
                }else{
                    cnt++
                }
            }
            if cnt & 1 == 1 {//判断最后一段连续的0
                st[i] = false 
            }
        }
        //预处理2
        var state[M][]int //某个状态j 所对应的k状态 共同作用下是一个合法的状态
        for j := 0; j < 1 << n; j ++ {
            for k := 0; k < 1 << n; k ++ {
                if j & k == 0 && st[j | k] {
                    state[j] = append(state[j], k)   
                }
            }
        }
        var f [N][M]int
        f[0][0] = 1
        for i := 1; i <= m; i ++ {//枚举每一列
            for j := 0; j < 1 << n; j ++ {
                for _, k := range state[j] {
                    f[i][j] += f[i-1][k]
                }
            }
        }
        fmt.Println(f[m][0])


    }
}