Dijkstra求最短路 I

主要是解释一下为什么dijkstra是由近及远来迭代

整个代码思路其实就是dijkstra的算法过程，具体代码意思注释有

如有不对之处，欢迎指出，十分感谢。

算法

Dijkstra算法的核心是由近及远，我们不用证明，直接看图。

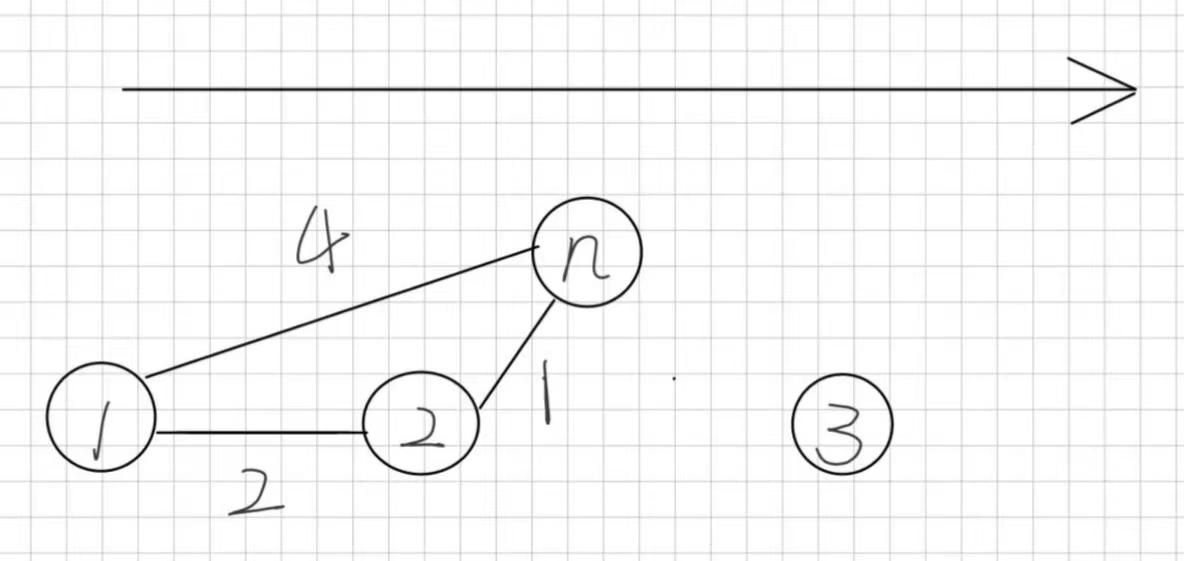
ps:线连接长度不是三角形，没有两边之和一定长于第三边定理，边长是取决于输入长度。
我们可以发现，在找最短路时，我们是不需要用到三号点的

同理

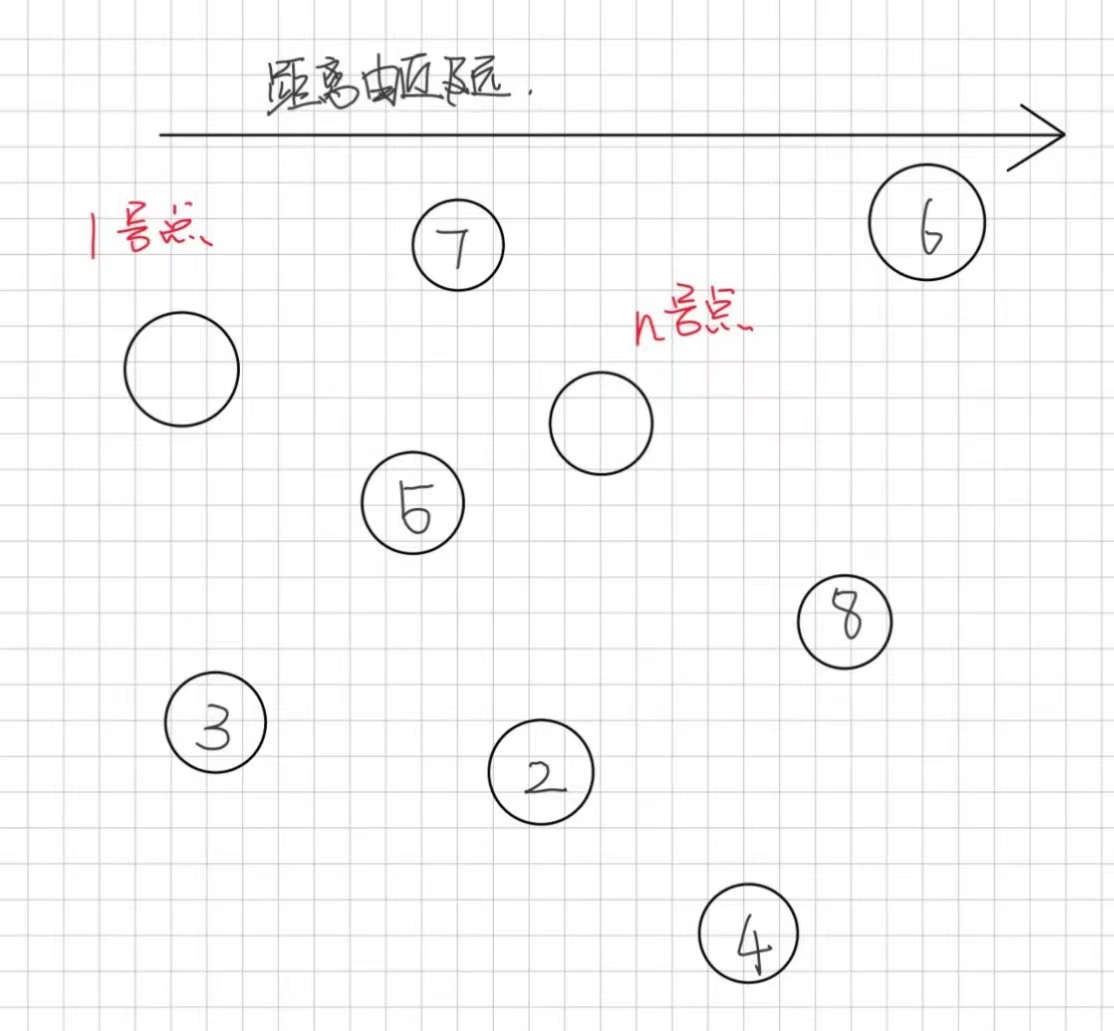
我们在找1号点到n号点的距离时，可以发现，n号点可能不是距离1号点最远的。

于是

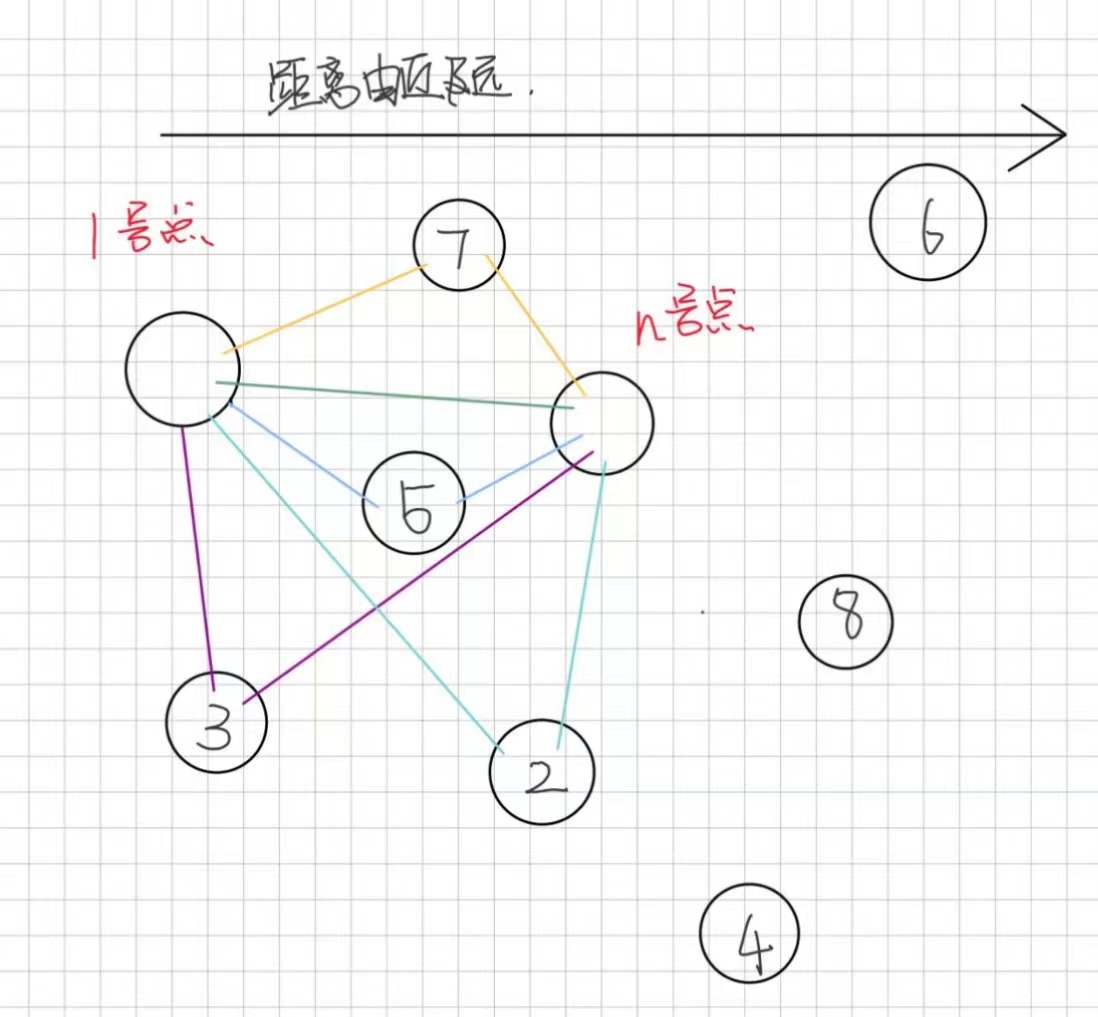
对于那些离1号点比n号点的点，例如：6，8，4对于求n号点最短距离是毫无用处的。
所以每一次迭代都是找还没标记过的离1号点最短的点，这样我们在处理最短路径时就完全不用考虑那些太远的点了。

那为什么要把所有的点都迭代过一遍呢。因为我们会面临1号点经历重重，磨难先经过好几个点才找到n号点的。
而经过的前几个点也有到前几个点的最短路径，所以，当我们把之前所有的点都迭代后，dist[]中记录的都是1号点到该点的最短距离，因此我们就可以找到最快的最短距离。
blablabla

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 510;

int n, m;
int g[N][N];
int dist[N];
bool st[N];

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    for (int i = 0; i < n - 1; i ++ ) //1号点和n - 1个点，n -1次循环
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
        {
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
            //如果该点还没被标记过，且(在它之前没有点了(这是为了避免之前没有记录点，就剩一个点) 或者 之前记录的最短的点都大于目前的点)
            //这是Dijkstra算法的核心，由远及近，层层扩展。
            //每次迭代都需要找还未标记的点的距离1号点最近的点。
            t = j;
        }

        for (int j = 1; j <= n; j ++ )
        {
            dist[j] = min(dist[j], dist[t] + g[t][j]);
            //找到某个点，看某个点到任一点的距离是否比从1号点的距离近
            //如果近，就输入到dist[j]
            //dist[j]只记录一号点到n号点的最短距离(可以绕路），不是1号点直达

        }

        st[t] = true;
        if (t == n) break;
    }


    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}


int main()
{
    scanf("%d%d", &n, &m);

    memset(g, 0x3f, sizeof g);
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);

        g[a][b] = min(g[a][b], c);//重边出现，选最短
    }

    printf("%d\n", dijkstra());

    return 0;
}