（数组建立邻接表） 树的dfs
//邻接表
int h[N], e[N * 2], ne[N * 2], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
树的bfs模板
// 需要标记数组st[N], 遍历节点的每个相邻的便
void dfs(int u) {
st[u] = true; // 标记一下，记录为已经被搜索过了，下面进行搜索过程
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!st[j]) {
dfs(j);
}
}
}
本题的本质是树的dfs， 每次dfs可以确定以u为重心的最大连通块的节点数，并且更新一下ans。
也就是说，dfs并不直接返回答案，而是在每次更新中迭代一次答案。
这样的套路会经常用到，在 树的dfs 题目中
详细注释
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10; //数据范围是10的5次方
const int M = 2 * N; //以有向图的格式存储无向图，所以每个节点至多对应2n-2条边
int h[N]; //邻接表存储树，有n个节点，所以需要n个队列头节点
int e[M]; //存储元素
int ne[M]; //存储列表的next值
int idx; //单链表指针
int n; //题目所给的输入，n个节点
int ans = N; //表示重心的所有的子树中，最大的子树的结点数目
bool st[N]; //记录节点是否被访问过，访问过则标记为true
//a所对应的单链表中插入b a作为根
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// dfs 框架
/*
void dfs(int u){
st[u]=true; // 标记一下，记录为已经被搜索过了，下面进行搜索过程
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(!st[j]) {
dfs(j);
}
}
}
*/
//返回以u为根的子树中节点的个数，包括u节点
int dfs(int u) {
int res = 0; //存储 删掉某个节点之后，最大的连通子图节点数
st[u] = true; //标记访问过u节点
int sum = 1; //存储 以u为根的树 的节点数, 包括u，如图中的4号节点
//访问u的每个子节点
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
//因为每个节点的编号都是不一样的，所以 用编号为下标 来标记是否被访问过
if (!st[j]) {
int s = dfs(j); // u节点的单棵子树节点数 如图中的size值
res = max(res, s); // 记录最大联通子图的节点数
sum += s; //以j为根的树 的节点数
}
}
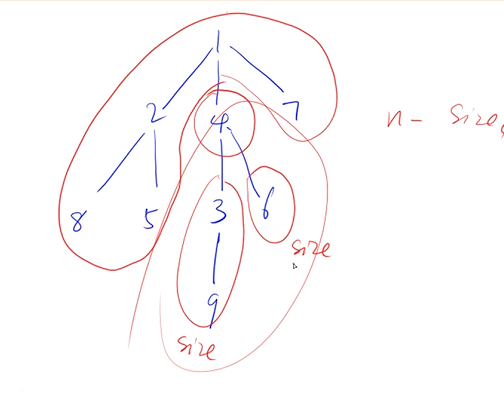
//n-sum 如图中的n-size值，不包括根节点4；
res = max(res, n - sum); // 选择u节点为重心，最大的 连通子图节点数
ans = min(res, ans); //遍历过的假设重心中，最小的最大联通子图的 节点数
return sum;
}
int main() {
memset(h, -1, sizeof h); //初始化h数组 -1表示尾节点
cin >> n; //表示树的结点数
// 题目接下来会输入，n-1行数据，
// 树中是不存在环的，对于有n个节点的树，必定是n-1条边
for (int i = 0; i < n - 1; i++) {
int a, b;
cin >> a >> b;
add(a, b), add(b, a); //无向图
}
dfs(1); //可以任意选定一个节点开始 u<=n
cout << ans << endl;
return 0;
}
我来补充一下，为什么 res = max(res, n - sum); 因为st数组标记是否被遍历，又因为main函数里dfs（1）这个1是随意的，所以就拿这题解上面的图，如果1开始，我们知道4是数的中心，而这时候遍历4的时候，因为1已经被遍历过了，所以res在for循环里不能往上走（不能往1那边走），那res = max(res, n - sum);就有用了
ps：如果嫌字小，按住ctrl滚鼠标中间放大
感谢，看到你的解释，终于解开了我的疑惑
感谢！！！！
牛 说得很清楚了
大佬太强了！自己想了半小时没明白，看到你的解释就懂了
大赞！！！
太，太太，太太太感谢啦!原来如此，我就说它不是遍历每一个和它相邻的结点么，为什么还要去算n-sum，原来是那个结点已经被标记为搜索过的点了，不用再搜了呀！！！妙，太妙了！！！
我还一直在想为什么不会忘上走，佬，我悟了
从4开始时确实会往上走，但他们举例时直接忽略了自己从1开始走的事实，这行迷惑代码浪费了我半天时间ಥ_ಥ
niubi thx!!!!
大佬，我有一点小疑惑，为什么是res=max(res,n-sum),为什么不是res=max(res,n-res)呢？，不是说res表示最大联通字节个数吗？
一开始的res是不包括u本身这一节点的，sum一开始初始化为1就是把u给包括进去了
orz
那如果我一开始就是从4开始呢？那不是还是会往上遍历，我还是没搞明白…
sum是每一次都会重置零吗
每一次dfs(u)时，sum都会初始化等于1（此时只有u一个点），在后续表示u点及其子树包括的节点数
这跟从哪里开始没关系。如果你4开始，n-sum就是0；然后你dfs(1)的时候，4走过了不会走了，那么n-sum就是4加上他的子树的节点了。
感谢，给你逮了两次哈哈哈哈
是每一次回溯再加上吗
dfs任意选数字是因为，这个图根本不存在孤立的点！随便挑个点，他都可以到达另外一个点。
不能从0开始是因为搞错了dfs参数u的意义，u不是idx（idx只是为了顺次排列这些数据），u是节点的编号，是从1开始的
为什么节点的编号是一定从1开始，不能是0吗？？
题目里说了 规定就是从1开始
巨佬我悟了
节点编号从1开始hh
我还有个疑问就是万一没有一这个节点呢
编号以此从1-n，如果连1这个点都没有那就没法做题了。
(¦3[▓▓]
哈哈哈哈哈哈，笑了
想问一下dfs遍历按顺序从左输出，该怎么弄，他这个刚好是从右边开始的
建立一个vis数组，有插入的点打上标记，然后一个for循环找到存在的第一个点，就选为你开始的root
兄弟我想问一下，for循环第一次i=h[1]=0, 每次i=ne[i]之后i不是还为h[1]（h[1]有0 1 2三个值）吗，是怎样执行下次循环遍历编号1的2 4 7三个子节点的？
还有就是add（a，b），add（b，a）两次add之后结点不就变成两倍了吗，有点没搞懂啊？
你说的两倍问题 变化的是根节点h[a] = idx++ 但节点上面的数字 h[a]=b 这个是没有变化的 idx可以想成是边上边的标号
插入数据的时候 h数组的值都变了呀
(¦3[▓▓]
idx相当于节点的地址，我们一开始设置出事地址是从$0$开始的idx到底是什么含义啊？整段代码中都没有对它进行赋初值
实际上是赋初值了，idx作为全局变量，自然就有0作为初始值。
另外，idx的含义就是为了顺次平铺这些数据到数组中，相当于给这些定了一个“地址”，地址就是idx，同时也是在数组里面的下标。
为什么main中只需要dfs(1)就可以了吗，不应该每个节点都删除一次找最小的ans吗？
标题是不是写错了“树的bfs模板”，应该是dfs？
那如果删除的是1这个点也就是树的根节点怎么理解呢
#### 如果对邻接表存储方式不太理解的同学，可以看看我的博文有详细解释
https://www.acwing.com/file_system/file/content/whole/index/content/4446359/
各位大佬们，为什么ans要初始化为N
N是n的最大值，同时不能初始化为n，在进入main函数前N就会完成初始化，此时n为0，那么ans也为0，这样就不对了
感谢，当初学习时不明白，现在已经通透~
不好意思为什么dfs()可以选任意数字
因为深度优先遍历从任何节点出发都会遍历到整个连通图呢
万一这里边没有一这个结点怎么办，那不就直接结束了吗
这道题目的题干中就写明了具有n个节点，且编号为1~n
如果有环怎么办？
有st数组判断是否被遍历过
这是无向树，任意点都可以是根
为什么dfs(0)是错的，dfs(-1)也能对
0是错的，因为编号从1开始，会将子树的节点个数返回。-1那个不会越界吗，但我试了试也能过，不知道为啥
因为数组会额外给你多开几个空间，并且都是初始为0，所以h[-1] = 0,然后这时候循环就是j = e[0] = 2(第一个存的结点idx，拿样例就是2)，然后dfs（2），就相当于dfs（2）从2开始递归，所以碰巧答案对了而已。
有多少人是从点分治来的
请问为什么返回sum而不是ans呢
因为sum表示的是以当前节点为根的节点数，如果当前节点没有被遍历过，就会一直递归遍历子节点，直到叶子节点时返回1，然后一直回溯叠加sum就能得到当前节点为根的节点数，而ans是通过比较直接赋值，不需要返回。我的理解是这样的
好的兄弟 谢谢你
不是树的$dfs$模板吗
不要在意这些细节~
既然是无向图，那给定一个节点必定会遍历所有和它相连的子节点，这样不就无所谓父子节点了。比如从4开始遍历的话，上面的和下面两个连通块点数都被计算过并被加到sum中。循环结束后res本来不就是最大连通块点数，,sum就是N了，那为什么还要max(n-sum,res)就不合理了。。
max(n-sum,res)对于首次遍历的节点来说是没必要的；但对后续的子节点dfs时由于已经过滤掉其父节点了，for循环中就不能获取到以父节点为根的子树，这种情况就需要max(n-sum,res)来保证
懂了 大佬太强了
👍
那为啥不直接把树看成有向图，add的时候只用add（a,b),不用add（b,a）了呀
看成有向图只能走一条路走到黑， 怎么能遍历到所有点呢
如果在主函数直接调用dfs(4）就相当于把4这个结点看成根节点，那么max(n-sum,res)显然是用不到的，因为for会把4的所有邻接点都访问，并且有int s = dfs(j);即4的每个邻接点子树的大小，但是这会把4这个根的邻接点都标记上已经被访问过了，接着你在二次递归的时候是没办法再回去的，只能以当前递归的到的点接着递归这个点的邻接点，那么父节点既然无法通过for来求出子树的数量，就可以通过n-sum，来求出。
举个栗子，假设主函数调用的是dfs（1），按照上面那个图，会以1这个点通过for来遍历邻接点，会有s=dfs(2),s=dfs(4),s=dfs(7)，你可以求出以1为重心的所有连通块的最大值，但是我刚才写的有一个s=dfs(2),你在dfs(2)的时候只能求出来2的所有未被访问的邻接点，也就是只能求出来dfs(5)和dfs(8)，求不出来以1为根的这个联通块的数量，这时候就只能通过总结点数n减去以2为根节点的数量来求出，也就是n-sum，然后在取一个max(n-sum,res)，就是以2为重心的最大连通块数量，这个难就难想在他是通过以一个点为起点开始递归，在递归的过程中求出res，再用res来更新ans，yxctql！
谢谢分享
妙啊
感谢感谢，懂了
谢谢，懂了。
感谢感谢！！例子解释的很好
大哥解释的很详细，赞
谢谢分享，又是一个小细节qaq
我发现一个点，就是我们在遍历一个节点的时候，先把根节点给st[u]给访问了，在遍历以u为根的邻接点的时候，就访问不到根节点这条邻接点的边了。
大佬太强了，一语点醒梦中人
应该是用st[i]标记了吧，假如从4开始，那么就不会向上递归到1因为1被标记为true了，时隔三年，兄弟应该理解透彻了
如果只用一个add(a,b)，在main函数里dfs开始的时候把dfs放在循环里dfs(i)，i为1到n的遍历，（我已经修改试过会错误）请问为什么这样不可以呢？求讲解
不知道我理解的对不对 本来dfs就是一个递归所有节点的函数 传n个参和传一个参没有区别
然后你用一个add显然不行 因为输入的只是表示两者有连线 没有方向（意思就是说这个实例输入可以任意颠倒前后位置，真正的结构可以画树来看 实际链表模拟是有方向的（包括遍历的时候））用两个add的话 由于!st[u]可以避免子节点递归母节点 所以不用担心算sum算超的风险
我帮你对加了一个add dfs用一个循环是能得到答案的 所以就是add的问题 dfs实际用一个就行
感谢回复，时间过去太久了有点忘了，晚会回顾一下
唔，我发现好像map[HTML_REMOVED]> f;也可以做领接表存图耶
为啥这里答案不对也ac了啊，我自己写的到这里答案也没对上，但是过了，有大佬知道是怎么回事吗
我把上课打的代码放进去说超时，别人的题解送进去答案也不对…
为什么dfs返回类型是int，但是在主函数里面没有接收也是对的
dfs返回int是用于int s = dfs(j);这一步，返回的值为用于求以当前节点的个个子树的节点数量
感谢！惊醒梦中人
请问如果不设置st[]会怎样？
死循环吧
谢谢！有道理
大佬，为什么idx不用初始化为0 呢
idx 是全局变量，默认从0开始
佬，最小的最大的连通子图是啥意思啊
最大是删除某个结点之后有许多连通块 此时的最大是删除某个节点后的剩下的所有连通块中点数最多的
最小是每个结点都对应有删除它之后的连通块的最大数 在所有节点的连通块的最大数中再取最小值
噢噢，懂了，谢谢
为什么dfs最后要返回sum呢
递归要走到头，然后依次返回更新，不返回，统计不了点的个数