C++ 代码
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 300010; //n次插入和m次查询相关数据量的上界
int n, m;
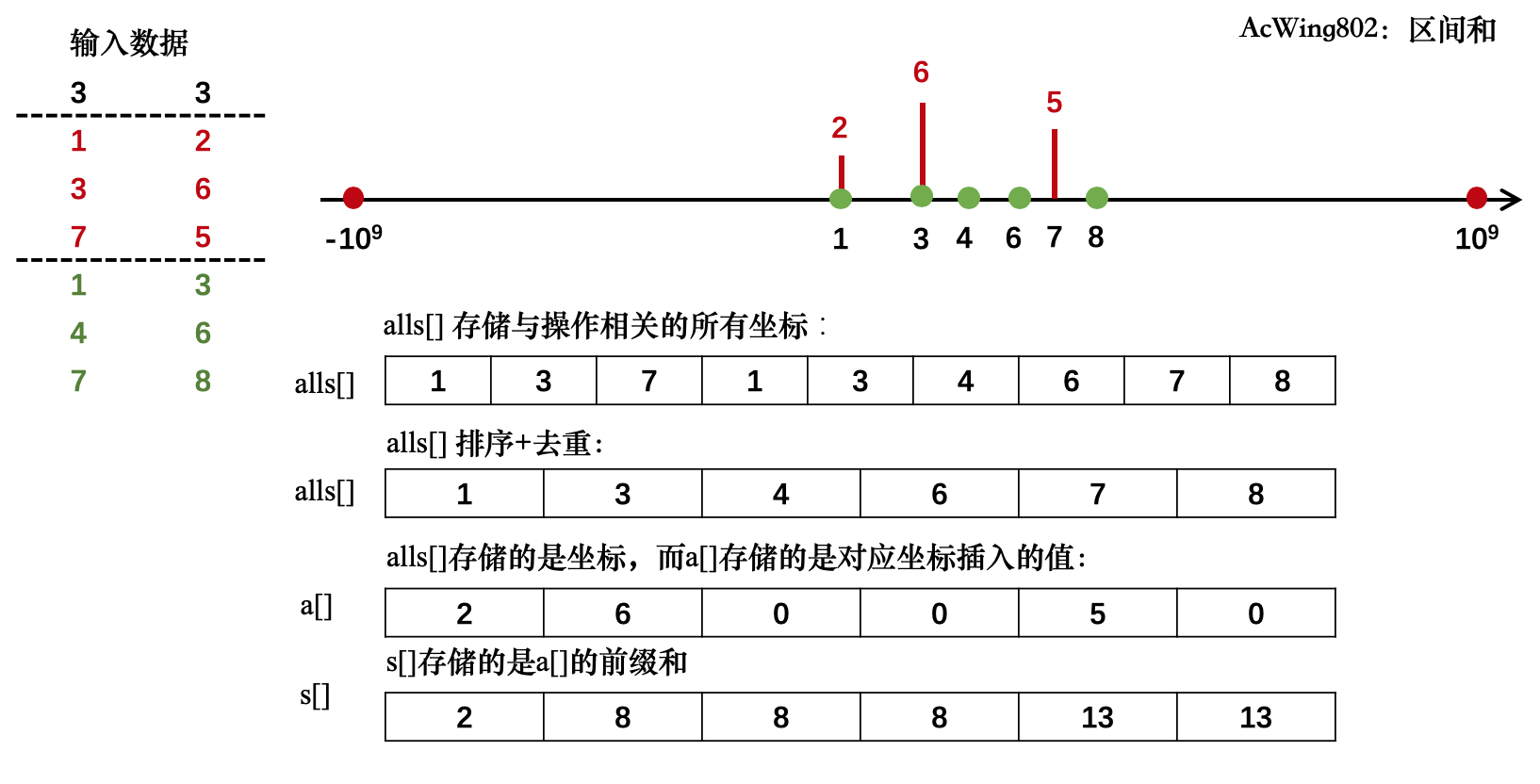
int a[N];//存储坐标插入的值
int s[N];//存储数组a的前缀和
vector<int> alls; //存储(所有与插入和查询有关的)坐标
vector<pair<int, int>> add, query; //存储插入和询问操作的数据
int find(int x) { //返回的是输入的坐标的离散化下标
int l = 0, r = alls.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
int x, c;
scanf("%d%d", &x, &c);
add.push_back({x, c});
alls.push_back(x);
}
for (int i = 1; i <= m; i++) {
int l , r;
scanf("%d%d", &l, &r);
query.push_back({l, r});
alls.push_back(l);
alls.push_back(r);
}
//排序,去重
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());
//执行前n次插入操作
for (auto item : add) {
int x = find(item.first);
a[x] += item.second;
}
//前缀和
for (int i = 1; i <= alls.size(); i++) s[i] = s[i-1] + a[i];
//处理后m次询问操作
for (auto item : query) {
int l = find(item.first);
int r = find(item.second);
printf("%d\n", s[r] - s[l-1]);
}
return 0;
}



我觉得第二张图的
index可以优化一下alls[]数组的index还是从0开始,而a[]数组和s[]数组的index从1开始。不过作者写的已经特别详细啦,感谢分享!
谢谢你~要不然我还蒙在鼓里(//̀Д/́/)
看见了r + 1还以为是板子背错了,结果发现数组下标不对应hh
orz, 贴一个不用find 的, 用哈希表记录下标
// 思路 : 因为范围太大, 所以不能开一个大数组 //开一个小数组 : 范围就是 add(index) + question(index) , 两者的范围, 排序去重 //我们在index + c, 就是要在新数组的新下标下标操作 #include<bits/stdc++.h> using namespace std; const int N = 1000010; int a[N], s[N]; typedef pair<int, int> pii; int main() { int n, m; cin >> n >> m; vector<pii> add, query; vector<int> all; for(int i = 0; i < n; i++) { int l , r; cin >> l >> r; add.push_back({l, r}); // 存储单独一个 all.push_back(l); } for(int i = 0; i < m; i++) { int l , r; cin >> l >> r; all.push_back(l); all.push_back(r); query.push_back({l, r}); } sort(all.begin(), all.end()); all.erase(unique(all.begin(), all.end()), all.end()); // 去重 unordered_map<int, int> get_index; //获取新下标 for(int i = 1; i <= all.size(); i++) get_index[all[i - 1]] = i; // 注意这里 all[i - 1] , 不是i for(int i = 0; i < add.size(); i ++){ int old_index = add[i].first; int c = add[i].second; int new_index = get_index[old_index]; a[new_index] += c; } for(int i = 1; i <= all.size(); i++){ a[i] += a[i - 1]; } for(auto p : query) { int l = p.first, r = p.second; int l2 = get_index[l], r2 = get_index[r]; cout << (a[r2] - a[l2 - 1]) << endl; } }写的不错,我也觉得用
unordered_map比find()更直观。不过输入
n组数据时,我觉得用x和c比l和r更好,后者看起来像坐标…另外,定义的前缀和数组
s[N]似乎没用到,你直接用了a[N]覆盖掉充当前缀和数组,感觉用s[N]更清楚些。为什么要去重啊,我没有去重也能过得?
//处理插入 for(auto item:add) { int x=get_index.at(item.first);//通过一个元素找到哈希表的另一个元素 a[x]+=item.second; } //处理前缀和 for(int i=1;i<=alls.size();i++) s[i]=s[i-1]+a[i]; //处理询问 for(auto item:query) { int l=get_index.at(item.first); int r=get_index.at(item.second); cout<<s[r]-s[l-1]<<endl; }贴一个用上s[N]数组的代码
废话(doge)
去没去重不影响最后的答案,事实上如果不选择去重,最后的运行时间还会少一些
测了一下,去重的版本跑了610+ms,没去重的反而只跑了580+ms
分析
以答主给出的代码为例
对于每个询问中给定的x和c,查找到的结果都是alls数组中x的左端点xl(例如,序列:1、1、2中元素1的左端点为0)
且每次都只会a[xl]上的元素操作,这意味着若alls中有一些下标:a1、a2、a3…ak,满足alls[a1] = alls[a2] = .... = alls[ak]
最后所有的操作都必定只会影响a[a1],因为a[a1]是左端点元素
因而,对于s中满足:alls[k1] = alls[k2] = .... = alls[kn]的连续下标:k1、k2…kn,只有a[k1]不等于0,其他下标的元素都为0
所以这种情况下,没有去重和去重之后每次询问得到的结果是一样的
再举个栗子
假设排序之后的alls是:1、1、3、3、4
去重之后是:1、3、4
执行操作“将x=1的元素加上2”后a数组是:2、0、0(索引从1开始计数)
前缀和数组应为:0、3、6、10(最开始的数值0代表没有元素被考虑累加的情况)
这时如果给出一个询问——l = 1, r = 3
那么find(l) = 1, find(r) = 2
所以结果为s[2] - s[1 - 1] = s[2] - s[0] = 6
而如果不去重呢?
此时alls是:1、1、3、3、4
执行操作“将x=1的元素加上2”后a是:2、0、0、0、0
前缀和数组应为:0、3、3、6、6、10
这时如果给出一个询问——l = 1, r = 3
那么find(l) = 1, find(r) = 2
所以结果为s[2] - s[1 - 1] = s[2] - s[0] = 6
前后结果保持不变
find(r)应该等于3吧
对,当时写错了O.O
没去重的话,那么重复的alls里面的数值会多次映射到数组a里面。但是我们二分分出来的是最左边的值,也就是说诸多重复的数值,只有最左边的数值的坐标映射到数组a里面,其余重复的数值映射的值都为0(显然会增加数组a的长度,占用空间)。仅仅是增加了数组a的长度,那自然不会影响前缀和的值
我优化了代码,重构了解释模式,希望可以帮助大家更好的理解😃~
#include <iostream> #include <vector> #include <algorithm> using namespace std; const int N = 300010; int a[N], s[N]; // a[] 存储对应坐标的值,s[] 是 a[] 的前缀和数组 vector<int> all_pos; // all_pos 存储原来真实(实际)坐标 real_pos unordered_map<int, int> pos_map; // pos_map 记录真实(实际)坐标 real_pos 到虚拟(离散化后的)坐标 virtual_pos 的“映射关系” vector<pair<int, int>> add, query; // add 记录加值操作,query 记录轮询操作 int main() { // 读入数据数据规模 int n, m; cin >> n >> m; // 读入 add 操作的数据 for (int i = 0; i < n; i++) { int x, c; cin >> x >> c; all_pos.push_back(x); // 先记录所有会用到的 real_pos,不管重复(后面会去重) add.push_back({x, c}); // 记录加值操作数据信息 } // 读入 query 操作的数据 for (int i = 0; i < m; i++) { int l, r; cin >> l >> r; all_pos.push_back(l); // 先记录所有会用到的 real_pos,不管重复(后面会去重) all_pos.push_back(r); // 先记录所有会用到的 real_pos,不管重复(后面会去重) query.push_back({l, r});// 记录轮询操作数据信息 } // 离散化 // 1. 排序 + 去重 sort(all_pos.begin(), all_pos.end()); // 排序 all_pos.erase(unique(all_pos.begin(), all_pos.end()), all_pos.end()); // 去重 // 2. 映射坐标 int virtual_pos = 1; // 为了方便前缀和计算,映射的坐标从 1 开始 for (auto real_pos : all_pos) { pos_map[real_pos] = virtual_pos; // 制作映射 virtual_pos++; } // 执行操作 // 1. add 操作 for (int i = 0; i < add.size(); i++) { int v_pos = pos_map[add[i].first]; // 获取 add 操作中的真实坐标 real_pos 对应的虚拟坐标 virtual_pos a[v_pos] += add[i].second; // 从 a[] 中取出坐标对应的值,然后加上 c 并重新存储 } // 2.1. 制作前缀和数组 for (int i = 1; i <= pos_map.size(); i++) { s[i] = s[i - 1] + a[i]; } // 2.2. query 操作 for (int i = 0; i < query.size(); i++) { int v_left = pos_map[query[i].first]; // 获取 add 操作中的真实坐标 real_pos 对应的虚拟坐标 virtual_pos int v_right = pos_map[query[i].second]; // 获取 add 操作中的真实坐标 real_pos 对应的虚拟坐标 virtual_pos int res = s[v_right] - s[v_left - 1]; // 计算本次轮询结果值 cout << res << "\n"; } return 0; }为什么alls要存储l与r呢?
答:我们最终要对[l, r]求和,自然就不能使用原来的数组求和(数据太大,过于离散)。
所以我们把l和r也映射到alls数组(l,r的值若没有add的操作,即插入不会在l或r的位置,值就为0(全局变量的默认值为0))。这样数轴就会变短很多(最大到3*10^5),我们就可以使用前缀和求和达到O(1)。
清晰易懂 我认为比前两个题解更好 tql
+1
确实,这篇画图讲解太清晰了
雀氏
yyds
+1
图解太棒了呀,赞
太棒了这个图。清晰易懂,大佬我可以搬一个到我打卡里面吗!!?
感谢哥,爱你
真厉害啊大佬,我测,我看了五天,看到你这一篇题解,真的突然明白了,太感谢了啊
,
为什么要将所需要使用的坐标进行排序和去重呢
我是这样理解的 all数组存放的是下标 既然是下标 那每一个下标都是唯一的 所以去重 排序是因为要使用二分查找 所以需要排序 不知道对不对😂
楼上看了一个帖子 可以不用去重
去重之后二分比较方便。(类似地,把查询操作里的 l 和 r 也一起维护进去,同样是方便写二分)
上述两点分别确保了我们查询的值 唯一 & 存在。这样在写二分时就可以统一按照
<x和>=x划分区间,找右侧分界点,此时该分界点一定就是那个值。假设没有唯一或者存在的前提,二分查找时就要额外考虑一些问题了。排序的话,是因为我们需要维护下标的全序关系。以这个题为例,它涉及到区间操作,所以我们要确保下标映射之后的顺序还是一样的。所以这里的因果关系是,进行了排序 -> 可以用二分查找。如果这里用 map 而不是二分的话,也是一样需要排序的。
讲的太透彻了,我想搬到我自己的博客可以么??追加链接嘿嘿
好多人盗他的题解,都盗到csdn上来,光今天我就看到四五篇
这道题解写的最好
// 本题思路来源
// 1、题目多次询问区间和,必定是用前缀和,但是发现范围太大,下标无法直接使用
// 2、下标一定是要离散化的,所以要用alls把所有用到的下标存起来,并且排序,然后利用相对大小关系排序
// 相对下标就是离散的结果。这就要用到排序,去重,二分。对应的是函数的使用以及二分find函数
// !!!!2要点是一个特别好的离散化思路,谨记
// 因为后期要用到前缀和,所以下标从1开始,二分返回结果要加1
// 同时添加和询问的一对数字是有一一对应关系的,所以还需要单独的结构来储存
// 结构选用的vector和pair以及结合,因为用到了vector的函数
这个是什么意思啊for (auto item : query) {
从头遍历query里面的所有元素,简单来说item=query[i]
这个为啥要排序去重啊
大佬牛p!!!
niubi
写的太棒了,二刷我原本也打算写个题解,一看你的觉得完全没有写的必要了。
这套功法太给力了, 直接让我成为金丹境
请问这个alls代表哪个英文单词啊,百思不得其解。
all+s,全部的
这图太清晰了吧 谢谢