题目描述
给定一个不重复的整数数组nums。最大二叉树可以用下面的算法从nums 递归地构建:
- 创建一个根节点,其值为nums 中的最大值。
- 递归地在最大值左边的子数组前缀上构建左子树。
- 递归地在最大值右边的子数组后缀上构建右子树。
返回nums 构建的 最大二叉树 。
示例 1:
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
示例 2:
输入:nums = [3,2,1]
输出:[3,null,2,null,1]
提示
1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同
递归
直接根据题目进行模拟,递归最多有n层,每一层都会遍历取得数组中的最大值,那么整体的时间复杂度为O(n2)
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func constructMaximumBinaryTree(nums []int) *TreeNode {
if len(nums) == 0{
return nil
}
maxIndex := maxInt(nums)
return &TreeNode{
Val: nums[maxIndex],
Left: constructMaximumBinaryTree(nums[:maxIndex]),
Right: constructMaximumBinaryTree(nums[maxIndex+1:])}
}
func maxInt(nums []int) int{
maxIndex := 0
for i:=1; i<len(nums); i++ {
if(nums[i] > nums[maxIndex]){
maxIndex = i
}
}
return maxIndex
}
笛卡尔树:单调栈建树 O(n)
笛卡尔树是一种二叉树,每个节点由一个键值二元组构成(k,w). 要求k满足二叉搜索树的性质,而w满足堆的性质。
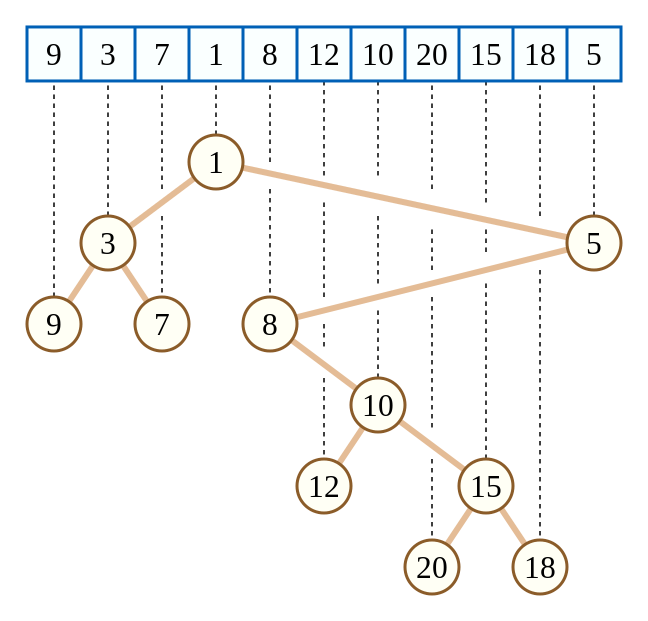
上面这棵笛卡尔树相当于把数组元素值当作键值w,而把数组下标当作键值k。那么k就满足二叉搜索树的性质,而键值w满足小根堆的性质。
上面这种特殊的笛卡尔树有一个性质,就是一棵子树内的下标是一个连续的区间(这样才能满足二叉搜索树的性质)。
这个题目其实就是一棵笛卡尔树的建树过程,堆是一个大根堆。那么就以大根堆为例,创建笛卡尔树。
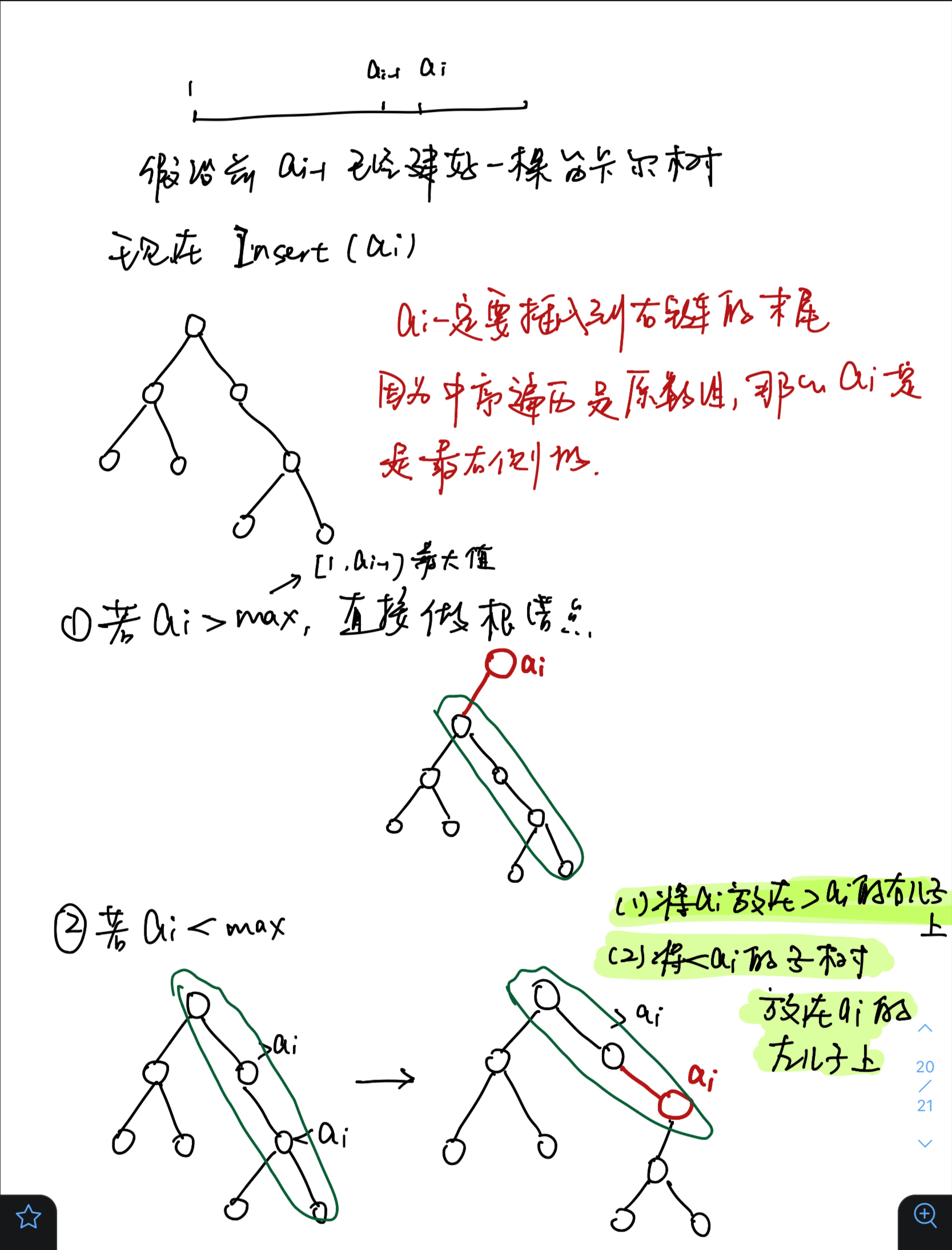
每次元素node都会先插入右链的末尾,然后从下往上遍历,如果当前节点比node节点的值小,就将以该节点为根的子树放到node节点的左子树上,直到找到第一个大于node的节点,将node节点作为该节点的右子树。
这个时候栈存储的是全部的右链节点,根节点位于栈的最底部。
这样每个节点最多进出一次,时间复杂度为O(n)。
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func constructMaximumBinaryTree(nums []int) *TreeNode {
var stack []*TreeNode
// index := 0
for _, num := range nums{
node := &TreeNode{Val: num}
for len(stack) > 0 && stack[len(stack)-1].Val < num{
node.Left = stack[len(stack)-1]
stack = stack[:len(stack)-1]
}
if len(stack) > 0 {
stack[len(stack)-1].Right = node
}
stack = append(stack, node)
}
return stack[0]
}

