对偶图
首先,题目一看就和割边集有关
所以我们要先把原图变成对偶图
原题中每条边的边权就是对偶图中该边两边的面间的边权
此题用vector做邻接表比较方便,所以为了用vector方便,要把二维的点映射到一维
inline int get(int x,int y){
return x*(m+1)+y;
}
将所有面映射完之后长这样:
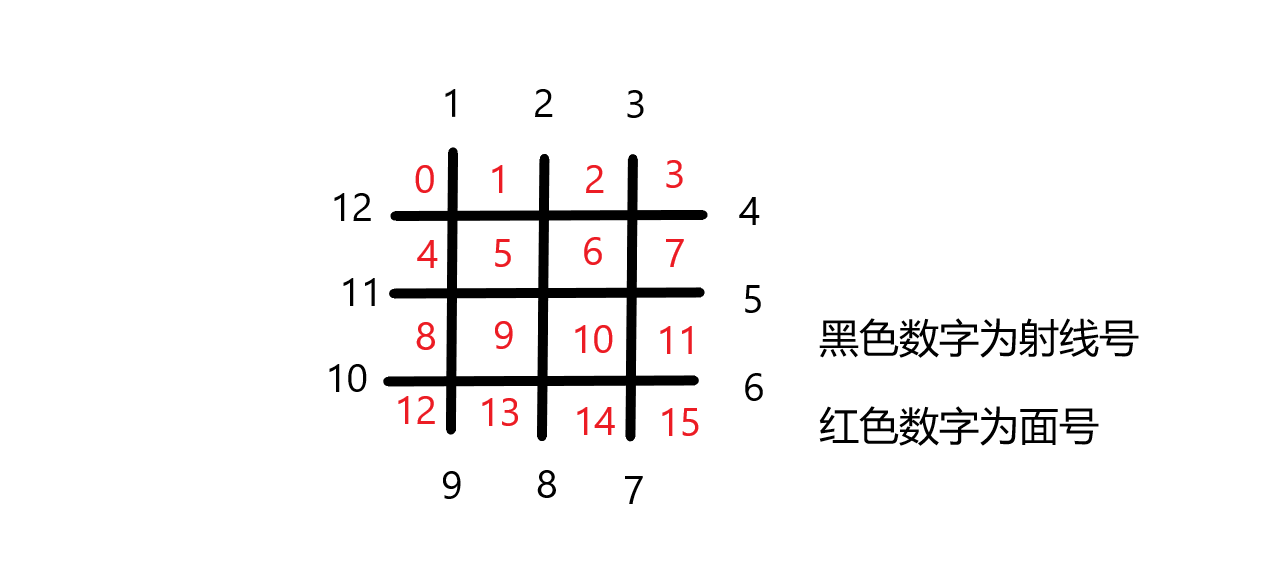
然后加入对偶图中的边
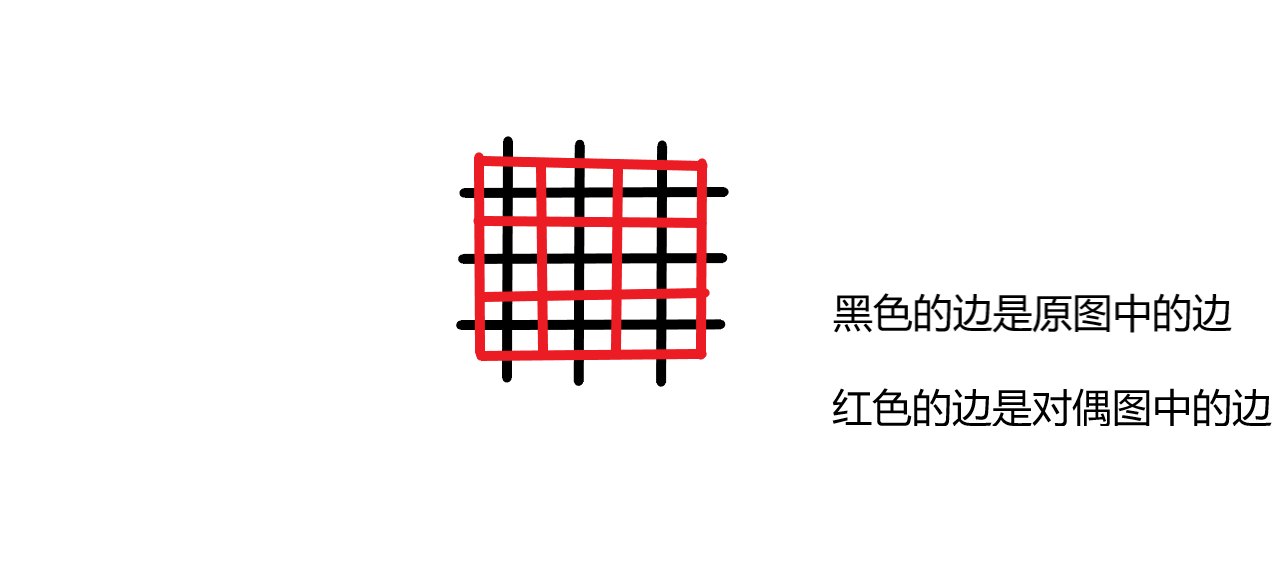
这里对储存射线间面连出去边的vector做一个特殊定义:
该vector的第1位代表该面与下一个射线间面的边
第2位代表该面与上一个射线间面的边
第3位代表该面与所处块之间的边(那个块具体是啥后面说)
四个角要先补一条边,充它们的第0位
如果在调用前没有push_back,vector会报错
所以所有射线间面都要补3条边,方便后面设置和处理
具体加边过程长这样:
for(int i=1;i<n;i++) //处理竖边
for(int j=1;j<=m;j++){
int w=read();
int x=get(i,j-1),y=get(i,j);
es[x].push_back({y,w});
es[y].push_back({x,w});
}
for(int i=1;i<=n;i++) //处理横边
for(int j=1;j<m;j++){
int w=read();
int x=get(i-1,j),y=get(i,j);
es[x].push_back({y,w});
es[y].push_back({x,w});
}
es[0].push_back({0,INF}); //四个角补一条充数用的边
es[m].push_back({0,INF});
es[rmap[n+m]].push_back({0,INF});
es[rmap[(m<<1)+n]].push_back({0,INF});
for(int i=1;i<=n+m<<1;i++) //射线间加三条充数用的边
for(int j=0;j<3;j++)
es[rmap[i]].push_back({0,INF});
色块
现在考虑题目所说的在射线上加点
比如这样:
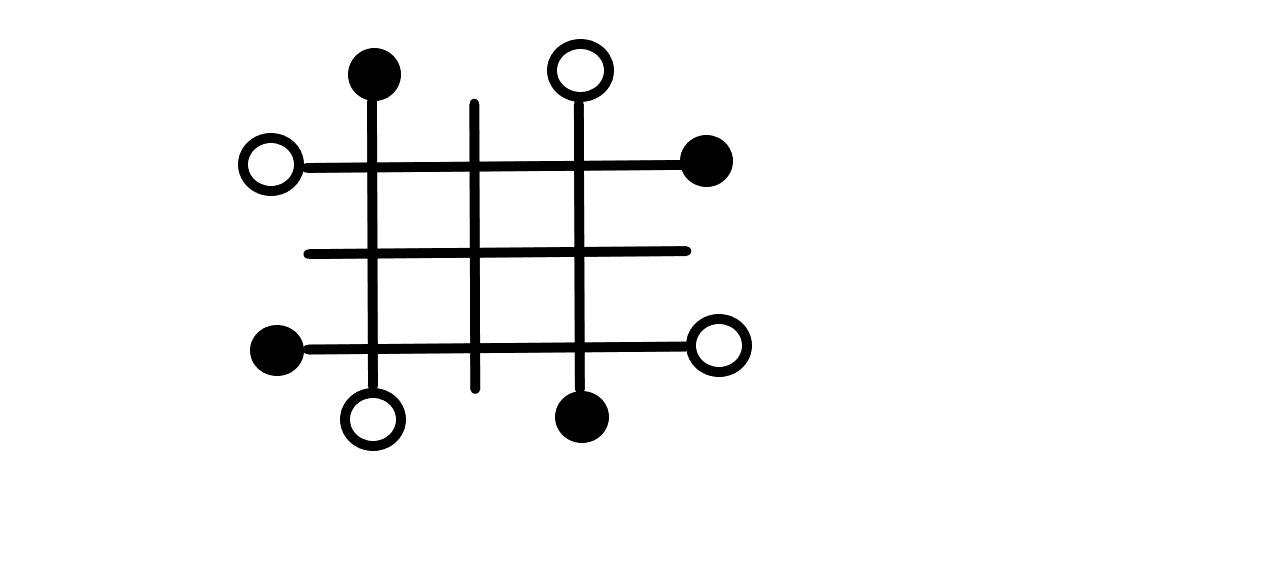
我们可以定义顺时针黑点到白点为红块,白点到黑点为蓝块
相邻的同色点可以认为它们在一个块里
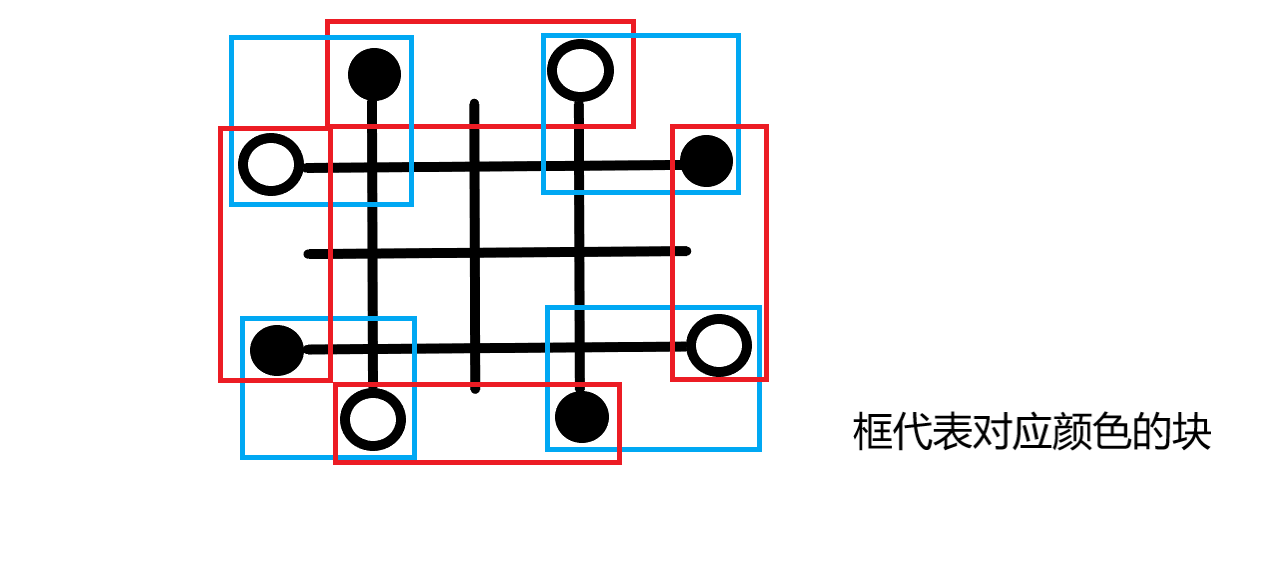
设置一些虚拟点,代表每一个块
然后这个虚拟点到块中所有射线间面的边权都为0
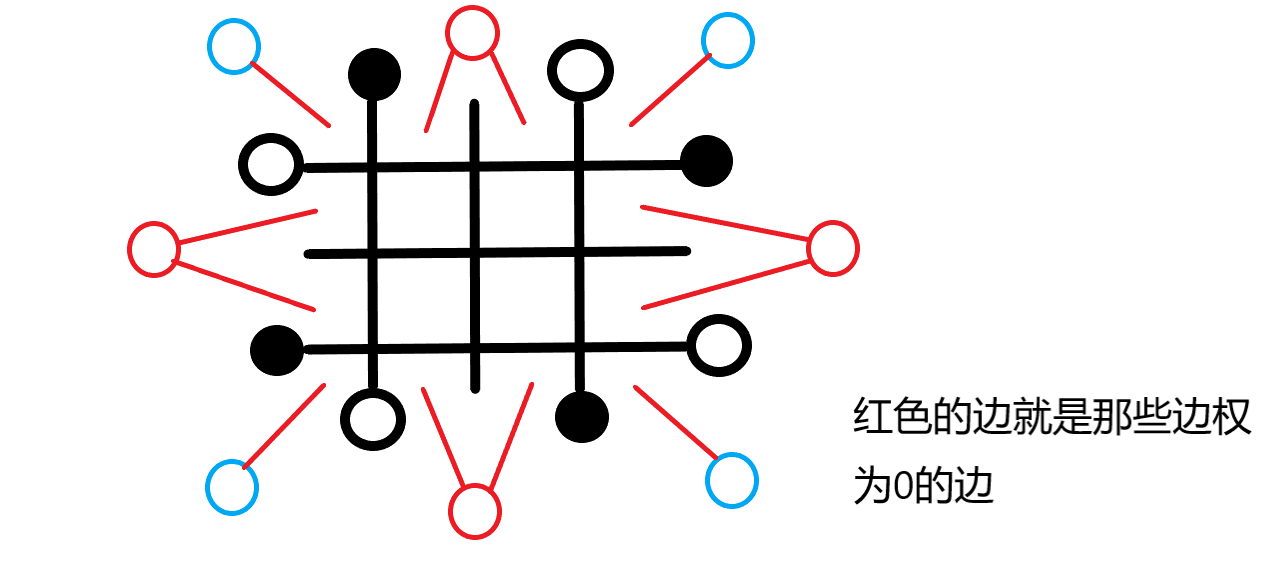
特判,如果没有块,直接输出0
加块和加块中边的代码长这样:
int bn=0; //储存块数
for(int i=0;i<k;i++){
int r=rs[i].r,w=rs[i].w,c=rs[i].c; //rs储存的是有点的射线的信息
es[rmap[r]][2]={rmap[r-1],w}; //设置射线间边权
es[rmap[r-1]][1]={rmap[r],w};
if(c==rs[(i+1)%k].c) //排除同色的情况
continue;
int nowb=(m+1)*(n+1)+bn++,nowr=rs[(i+1)%k].r;
while(r!=nowr){ //在一个块间加入边权为0的边
es[nowb].push_back({rmap[r],0}); //es存的是边
es[rmap[r]][3]={nowb,0};
r=r%(n+m<<1)+1;
}
}
if(bn==0){ //没有块的情况下直接输出
puts("0");
continue;
}
所有的块会构成一个环,相邻的一定异色
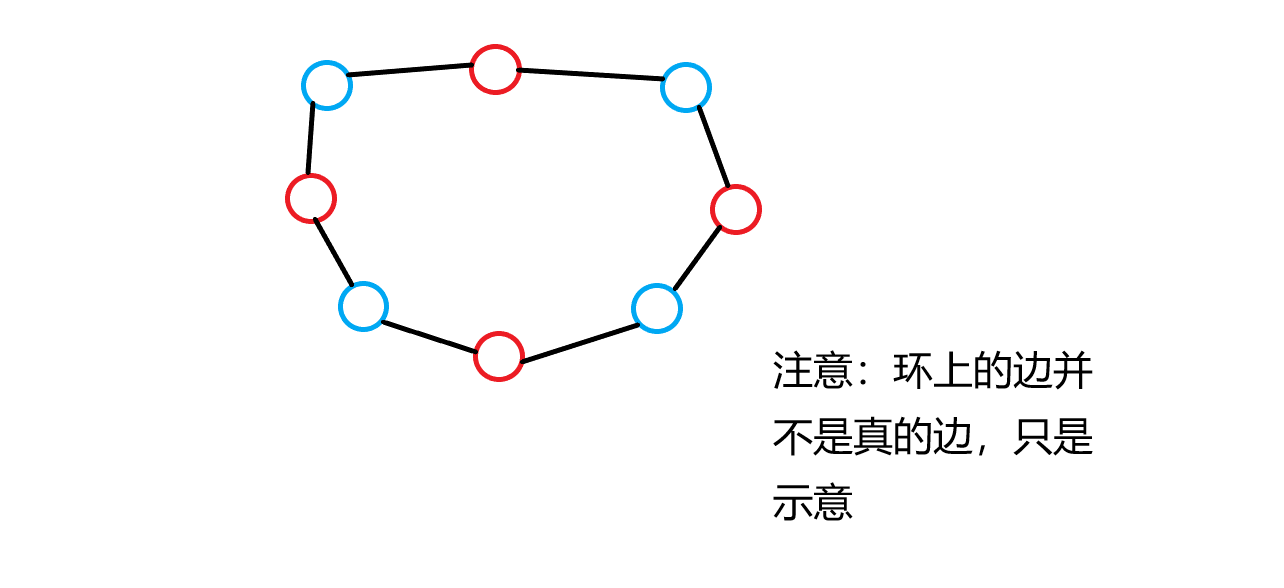
dijkstra
在对偶图上将异色块间的最短距离算出来
g[i][j]代表i号块到j号块的最短距离(前提:i号块和j号块异色)
memset(g,0,sizeof g);
for(int i=0;i<bn;i+=2){
dijkstra((m+1)*(n+1)+i); //以该块为起点做dijkstra
for(int j=1;j<bn;j+=2) //红蓝块是相间的,所以两个相邻块一定异色
g[i][j]=g[j][i]=dist[(m+1)*(n+1)+j];
}
下面是dijkstra堆优化模板
inline void dijkstra(int s){ //堆优化dijkstra模板
memset(dist,0x3f,sizeof dist);
dist[s]=0;
que.push({0,s});
while(que.size()){
int now=que.top().second;
que.pop();
for(int i=0;i<es[now].size();i++){
int t=es[now][i].t,w=es[now][i].w;
if(dist[now]+w<dist[t]){
dist[t]=dist[now]+w;
que.push({dist[t],t});
}
}
}
}
区间DP
将异色块进行两两配对
f[i][j]代表处理完i号块到j号块后得出的最短距离(i号块和j号块异色)
于是我们得出转移方程:
设k为i+3~j-3之间的一个点
f[i][j]=min(g[i%bn][k%bn]+f[i+1][k-1]+f[k+1][j])
这里有两种特殊情况:
1.i号块和j号块配对
g[i%bn][j%bn]+f[i+1][j-1]
2.i号块和i+1号块配对
g[i%bn][(i+1)%bn]+f[i+2][j]
区间DP的代码长这样:
for(int i=0;i<(bn<<1)-1;i++) //构成环状
f[i][i+1]=g[i%bn][(i+1)%bn];
for(int len=4;len<=bn;len++) //区间DP
for(int i=0,j=i+len-1;j<(bn<<1)-1;i++,j++){
f[i][j]=min(g[i%bn][j%bn]+f[i+1][j-1],g[i%bn][(i+1)%bn]+f[i+2][j]);
for(int k=i+3;k<j-2;k+=2)
f[i][j]=min(f[i][j],g[i%bn][k%bn]+f[i+1][k-1]+f[k+1][j]);
}
完整代码
完整代码有亿点长
需要耐心才能看完
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N=252005,INF=0x3f3f3f3f;
struct edge{
int t,w;
};
struct ray{
int w,r; //分别储存和相邻点的边权、射线编号和颜色
bool c;
bool operator<(const ray &W)const{
return r<W.r; //按射线编号排序
}
}rs[55];
int n,m,t;
int rmap[2005]; //存储射线间的面号
int g[55][55],dist[N],f[55][55]; //储存块间的距离、中间结果和区间DP
vector<edge> es[N]; //边
priority_queue<PII,vector<PII>,greater<PII>> que;
inline int read(){ //快读
char x=getchar();
int res=0;
while(x<'0'||x>'9')
x=getchar();
while(x>='0'&&x<='9'){
res=res*10+x-'0';
x=getchar();
}
return res;
}
inline int get(int x,int y){ //二维到一维
return x*(m+1)+y;
}
inline void build(){ //将射线号对应到射线之间的面号
for(int i=1;i<=m;i++)
rmap[i]=get(0,i);
for(int i=m+1;i<=n+m;i++)
rmap[i]=get(i-m,m);
for(int i=n+m+1;i<=(m<<1)+n;i++)
rmap[i]=get(n,(m<<1)+n-i);
for(int i=(m<<1)+n+1;i<=m+n<<1;i++)
rmap[i]=get((m+n<<1)-i,0);
rmap[(m+n<<1)+1]=1; //形成环状
}
inline void dijkstra(int s){ //堆优化dijkstra模板
memset(dist,0x3f,sizeof dist);
dist[s]=0;
que.push({0,s});
while(que.size()){
int now=que.top().second;
que.pop();
for(int i=0;i<es[now].size();i++){
int t=es[now][i].t,w=es[now][i].w;
if(dist[now]+w<dist[t]){
dist[t]=dist[now]+w;
que.push({dist[t],t});
}
}
}
}
int main(){
n=read();
m=read();
t=read();
build();
for(int i=1;i<n;i++) //处理竖边
for(int j=1;j<=m;j++){
int w=read();
int x=get(i,j-1),y=get(i,j);
es[x].push_back({y,w});
es[y].push_back({x,w});
}
for(int i=1;i<=n;i++) //处理横边
for(int j=1;j<m;j++){
int w=read();
int x=get(i-1,j),y=get(i,j);
es[x].push_back({y,w});
es[y].push_back({x,w});
}
es[0].push_back({0,INF}); //四个角补一条充数用的边
es[m].push_back({0,INF});
es[rmap[n+m]].push_back({0,INF});
es[rmap[(m<<1)+n]].push_back({0,INF});
for(int i=1;i<=n+m<<1;i++) //射线间加三条充数用的边
for(int j=0;j<3;j++)
es[rmap[i]].push_back({0,INF});
while(t--){
int k=read();
for(int i=0;i<k;i++){
rs[i].w=read();
rs[i].r=read();
rs[i].c=read();
}
for(int i=1;i<=n+m<<1;i++){ //还原射线间的边
es[rmap[i]][1]={rmap[i+1],0};
es[rmap[i]][2]={rmap[i-1],0};
es[rmap[i]][3]={0,INF};
}
sort(rs,rs+k); //按一圈排序
int bn=0; //储存块数
for(int i=0;i<k;i++){
int r=rs[i].r,w=rs[i].w,c=rs[i].c;
es[rmap[r]][2]={rmap[r-1],w}; //设置射线间边权
es[rmap[r-1]][1]={rmap[r],w};
if(c==rs[(i+1)%k].c) //排除同色的情况
continue;
int nowb=(m+1)*(n+1)+bn++,nowr=rs[(i+1)%k].r;
while(r!=nowr){ //在一个块间加入边权为0的边
es[nowb].push_back({rmap[r],0});
es[rmap[r]][3]={nowb,0};
r=r%(n+m<<1)+1;
}
}
if(bn==0){ //没有块的情况下直接输出
puts("0");
continue;
}
memset(g,0,sizeof g);
for(int i=0;i<bn;i+=2){
dijkstra((m+1)*(n+1)+i);
for(int j=1;j<bn;j+=2)
g[i][j]=g[j][i]=dist[(m+1)*(n+1)+j];
}
for(int i=0;i<(bn<<1)-1;i++) //构成环状
f[i][i+1]=g[i%bn][(i+1)%bn];
for(int len=4;len<=bn;len++) //区间DP
for(int i=0,j=i+len-1;j<(bn<<1)-1;i++,j++){
f[i][j]=min(g[i%bn][j%bn]+f[i+1][j-1],g[i%bn][(i+1)%bn]+f[i+2][j]);
for(int k=i+3;k<j-2;k+=2)
f[i][j]=min(f[i][j],g[i%bn][k%bn]+f[i+1][k-1]+f[k+1][j]);
}
int ans=INF;
for(int i=0;i<bn;i++)
ans=min(ans,f[i][i+bn-1]);
printf("%d\n",ans);
for(int i=0;i<bn;i++)
es[(m+1)*(n+1)+i].clear();
}
return 0;
}
O3优化
注意:
因为一些玄学的原因,这段代码是会TLE的!!
开O3优化才可以过(O2没试过,有兴趣的人可以自己试试)
目前还木有找到不开O3能过的方法……
想通过的人把这句代码加到完整代码的前面
#pragma GCC optimize(3,"Ofast","inline")

