将每一个h[i]的所有方案看做是一张有向图,例
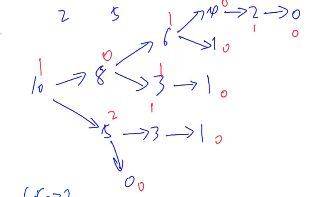
若S=[2,5],h=10,则有如下展开形式:
mex():设集合S是一个非负整数集合,定义mex(S)为求出不属于S的最小非负整数的运算,即:mes(S)=min[x],其中x属于自然数,且x不属于S(用人话说就是不存在S集合中的数中,最小的那个数)
SG():在有向图中,对于每个节点x,设从x出发共有k条有向边,分别达到节点y1,y2……yk,定义SG(x)为x的后继节点的SG值构成的集合执行mex()运算后的值
即:SG(x)=mex(SG(y1),SG(y2)…SG(yk));(用人话说就是比后继节点的SG都小的值)
特别的整个图G的SG值被定义为起点s的SG值,即SG(G)=SG(s)
上图标红的值就是每一个节点的SG值
性质:1.SG(i)=k,则i最大能到达的点的SG值为k−1。
2.非0可以走向0
3.0只能走向非0
定理:
对于一个图G,如果SG(G)!=0,则先手必胜,反之必败
证明:
若SG(G)=!0,
1.根据性质2,先手必可以走向0,
2.因此留给后手的是0,根据性质3,后手只能走向非0
3.以此类推,后手始终无法走向0,后手永远处于非0,当先手到达终点的0时,先手获胜
(由此我们可以知道,有些事是命中注定的~~~)
反之同理,必败
定理:
对于n个图,如果SG(G1) ^ SG(G2) ^ … SG(Gn)!=0 ,则先手必胜,反之必败
证明(类似与Nim游戏):
①当SG(Gi)=0 时 , xor=0 , 显然先手必败
(PS:结束状态必是状态①,但状态①不一定是结束状态)
②当xor=x!=0 时,因为肯定存在一个SG(xi)^x <SG(xi),而根据SG()的性质1可知,SG(k)可以走到0−k−1的任何一个状态,
因此,必定可以从SG(xi)−>SG(xi)^x , 于是使得xor=0
③当xor=0时,当移动任何一个节点时,对应的SG值必然减小,可以证明:xor!=0
下证:xor!=0
假设:xor=0,则说明移动的那个节点的值并没有变化,即从SG(k)变成了k,但是这与SG函数的性质1相矛盾,因此不成立
证得:若先手面对的状态是xor!=0,则先手方总能使xor=0,即使后手面对的永远是必败态直到结束状态①,因此先手必胜!
反之,必败!
C++ 代码
#include <iostream>
#include <unordered_set>
#include <cstring>
using namespace std;
const int N = 110 , M = 10010;
int n , m;
int s[N] , f[M];
int sg(int x)
{
if(f[x] != -1) return f[x];//记忆化搜索,如果f[x]已经被计算过,则直接返回
// 因为这题中较大堆的拆分情况独立于较小堆,因此有别于894.拆分-Nim,这里的S必须开成局部变量
unordered_set<int> S;//用一个哈希表来存每一个局面能到的所有情况,便于求mex
for(int i = 0 ; i < m ; i++)
if(x >= s[i]) S.insert(sg(x - s[i]));//如果可以减去s[i],则添加到S中
for(int i = 0 ; ; i++)//求mex(),即找到最小并不在原集合中的数
if(!S.count(i)) return f[x] = i;
}
int main()
{
cin >> m;
for(int i = 0 ; i < m ; i++) cin >> s[i];
memset(f , -1 , sizeof f);
cin >> n;
int res = 0;
while(n--)
{
int x;
cin >> x;
res ^= sg(x);
}
if(res) puts("Yes");
else puts("No");
return 0;
}


有一个错误,应该是SG(i)=k,那么i一定能走到0~k-1的所有状态,且i走不到k这个状态,
SG的值不一定时变小,别的都很棒!
从i点走一步后,SG的值一定变小
楼主距离的图中10走到5,SG的值就变大了啊
感谢指正错误~hh,是这样的,及时拉我一把
大佬,想问一下,SG函数的性质中,SG(i)=k,为啥则i最大能到达的点的SG值为k−1?比如文中图片的SG(10)=1,但它连接的子节点中SG(5)=2呀
他这个想表述的应该是i在小于k时所能达到的点的SG值最大为k-1,SG所要求的是所不含有的自然数中的最小值,也可能有比k大的
写错了吧,应该是
SG(i)=k-1,则i最大能到达的点的SG值为k
我认为应该是:若SG(i) = k , 那么一定可以走到0 ~ k - 1 的任一个值,但大于k的值可能走到也可能走不到。因为SG(i)的值是根据其子节点的SG值得来的。
/bx 写的很好
写的很好!
大佬,想问一下,sg函数 最后 return的是 fx=i,那sg是怎么赋值的呢,向S里插入sg(x-sum),sg(0)等于多少呢?
f[]就是sg的值呀,sg(0)=0可是 最后不是赋值的 是 f[x]=i吗,这是个等式 也不是 一个值啊,最后sg[x]也是返回 i?
对呀,(f[x]=i)会返回i,这不是基本语法吗😅
555 真的不知道 看着好难理解
加油
谢谢大佬
如果找到最小不存在S中的值会直接reutrn
for(int i = 0 ; ; i++)。没有限制循环终止条件,如何停止?谢谢大佬
你不看看这一句下面有return嘛?
大佬,能帮我看看代码吗
#include<bits/stdc++.h> using namespace std; const int N=1e6; int sum[N],f[N];//f[]保存sg的函数值,sum[]保存可以由那个状态转移过来 int n,m; int res; set<int>S; int sg(int x) { if(f[x]!=-1) return f[x];//如果当前点的sg值已经计算过,直接返回,保证时间复杂度 S.clear(); for(int i=0;i<m;i++) { int t=sum[i]; if(x>=t) S.insert(sg(x-t)); } for(int i=0;;i++) { if(!S.count(i)) { return f[x]=i; } } } int main() { cin>>m; for(int i=0;i<m;i++) cin>>sum[i]; memset(f,-1,sizeof(f)); cin>>n; for(int i=1;i<=n;i++) { int x; cin>>x; res^=sg(x); } if(res>0)cout<<"Yes"<<endl; else cout<<"No"<<endl; }唯一一点不同的地方就是我把判断元素是否存在的set放在全局变量里,然后每次进行清空,不知道这样做有什么问题
你这样是不行的,你看看逻辑结构,你这样写每次用的S都是同一个,但是我的代码里是每次调用函数的时候重新声明一个不一样的S。
你可以模拟一下你的代码,你声明了一个全局的S,以后每次找到的数都是丢到同一个S里,这样显然是不对的,因为后面的点所能到的局面跟前面的点是不一样的,肯定要为后面的点重新声明一个新的S,来表示之后所能到的局面。
你应该没有理解这个递归,回复不及时抱歉hh~
谢谢大佬解答,但是我还有个问题没搞懂,就是我每次我求该点的sg函数值的时候,我把S清空了,我觉得定义在全局变量并清空,和在每次调用函数的时候,再重新定义一个set应该是一样的吧。
那在回溯的时候会用到原来声明的S。就比如说在点1时声明了一个S1,在点2的时候声明了一个S2,你如果直接clear() S,那不就把之前的S1、S2清空了,但其实在回溯的时候还是会用到S1、S2的,看似声明的都是S,其实是不一样的。你还是没太理解递归。
递归该怎么理解,我确实有点该不太懂,不知道递归的具体实现过程是怎么样的,能具体说一下吗,谢谢大佬
(最经典的递归就是dfs,你可以再看看dfs)
在递归的过程中你声明了一个S,那么这个S就属于这一层递归,即使我们在下一层递归中又声明了S,但是这个S非彼S,你可以理解为S1、S2、S3等。
递归另一个重要点就是回溯,回溯就是在执行完下面那层递归之后返回上一层递归,然后继续执行下面的代码,写递归得要好好考虑回溯的过程应该干什么。
谢谢大佬,受益颇多
加油hh~
我是前几天自己debug才理解这个递归申明的变量属于某一层的
加油
为什么一定存在一个可以取得石子数目,使得取后,数目变为 SG(x2)^m
哪一块的证明里呀
” ②当xor=x!=0时,因为肯定存在一SG(xi)^x [HTML_REMOVED]SG(xi)^x , 于是使得xor=0 “
作者解释得很好,顶一个^v^~~~~
如果sg1^sg2^sg3^.......^sgn!=0(=x),即先手必胜,则一定存在一个sgi可以使得sgi转化为sgi^x,即后手必败。求得sgi可以转化的每一种状态后,利用mex()集合求sgi的值,sgi的值为sgi通过一步转化可以到达的所有sgy的集合的mex()的值,根据mex()集合的定义,若sgi的值不为0,则sgi可以转化至0~sgi中的任意值,0~sgi
中就包括sgi^x,则可以保证先手必胜。
如图,sg10通过一步转化可以到达的所有sgy的集合为sg8,sg5,sg10=mex(sg8,sg5)=1。
哈哈 这个在Nim游戏证明的比较详细
嗯嗯,一起加油^v^~~~~
大佬,代码中
int sg(int x) { if(f[x] != -1) return f[x];//记忆化搜索,如果f[x]已经被计算过,则直接返回 unordered_set<int> S;//用一个哈希表来存每一个局面能到的所有情况,便于求mex for(int i = 0 ; i < m ; i++) if(x >= s[i]) S.insert(sg(x - s[i]));//如果可以减去s[i],则添加到S中 for(int i = 0 ; ; i++)//求mex(),即找到最小并不在原集合中的数 if(!S.count(i)) return f[x] = i; }unordered_set[HTML_REMOVED] S;每次计算新的一个点的后继的话,用不用清空
每次unordered_set在你调用sg函数时候都会在栈空间新开一个 不用考虑清空 因为你用的是递归