1.最小生成树与最短路的区别

最小生成树：把连通的图的所有顶点连起来路径之和最小的问题，即生成树总权值之和最小。

最短路：把两点之间路径最短。

最短路只是需要将两个点连起来，其路径并不一定经过所用点，而最小生成树要连接每一个点

eg： 下图中，A->D的最短路= AC+CD ； 最小生成树 = AC+CD+AB

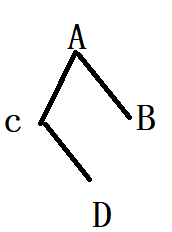
2.prim 与 dijkstra 思路区别

dijkstra：把所有点到 源点 距离dis设成∞ ，每次找到dis最小的点 确定下来(加入到路径中)，并用该点距离更新所有点到源点距离 dis[i]=min(dis[i],w+a[t][i]);
即：用源点扩展，每次确定距离最近的点，直到终点！！

prim： : 把所有点到 集合 的距离dis设成∞ ，每次找到dis最小的点 确定下来(加入到集合中)，并用该点距离更新所有点到集合距离 dis[i]=min(dis[i],a[t][i]);
即：随意找一个起点，每次确定到集合最近的点，直到所有点都确定完！！

由上面的思路区别，不难看出唯一区别就是，dijkstra 更新的是到源点的距离，prim更新的是到集合的距离。

3.prim 与 dijkstra 代码区别

由上面可知 dijkstra和prim 的唯一区别，那是不是只需要将dijkstra代码中的 dis 更改成到集合的距离就可以了？像下面这样：

试过之后发现并不能AC。

其实思路并没错，只是prim 是到集合的距离，所以后面的点可能会更新前面已经确定点的距离，不像dijstra是到源点的距离后面的距离定这会更大，不会更新前面的dis
eg： q为队列中放内容

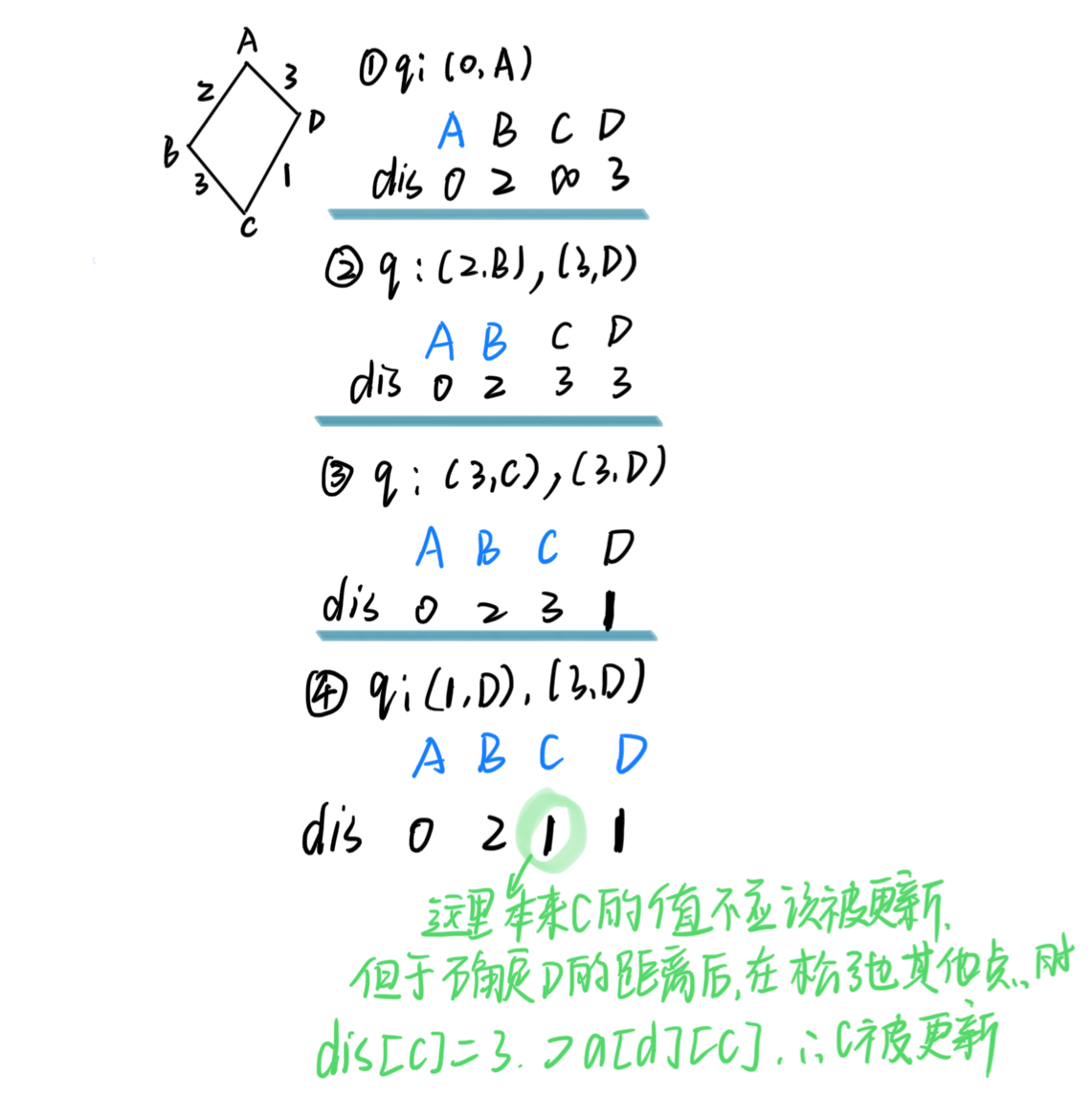
综上所述：只需要将已经确定的点的dis不在被改变即可：

void bfs()
{
    priority_queue<PII,vector<PII>,greater<PII>> q;
    memset(res,0x3f,sizeof res);    
    res[1]=0;
    q.push({0,1});
    while(q.size())
    {
        auto t=q.top();
        q.pop();
        if(st[t.second]) continue;
        st[t.second]=true;

        for(int i=h[t.second];i!=-1;i=ne[i])
        {
            int k=e[i];
            if(res[k]>w[i]&&!st[k]) //这里加个标记
            {
                res[k]=w[i];
                q.push({res[k],k});
            }
        }
    }
}

4.关于prim细节

1. y总的代码在统计总和时是在 确定每个点后加上res+=dis, 并不能等到最后在遍历 求dis的总和原因如上第三个标题
2. prim和dijkstra 都是差不多都是基于 bfs 思路
3. 具体代码： 下面存边用的时邻接表存的，主要是为了更好区别dijstra，用邻接矩阵松弛操作直接for循环遍历每个点即可。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>

using namespace std;

typedef long long LL;
typedef pair<LL ,LL >PII; 
const int N=1e6;

LL n,m,resmax;
LL e[N],ne[N],w[N],idx=0,h[N];
LL res[N];
bool st[N];

void add(int a,int b,LL ww)
{
    e[idx]=b,ne[idx]=h[a],w[idx]=ww,h[a]=idx++;
}

void bfs()
{
    priority_queue<PII,vector<PII>,greater<PII>> q;
    memset(res,0x3f,sizeof res);    
    res[1]=0;
    q.push({0,1});
    while(q.size())
    {
        auto t=q.top();
        q.pop();
        if(st[t.second]) continue;
        st[t.second]=true;

        for(int i=h[t.second];i!=-1;i=ne[i])
        {
            int k=e[i];
            if(res[k]>w[i]&&!st[k])
            {
                res[k]=w[i];
                q.push({res[k],k});
            }
        }
    }
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    cin>>n>>m;
    memset(h,-1,sizeof h);

    for(int i=0;i<m;i++)
    {
        LL a,b,ww;
        cin>>a>>b>>ww;
        add(a,b,ww);
        add(b,a,ww);
    }
    bfs();

    for(int i=2;i<=n;i++) 
    {
        resmax=resmax+res[i];
        if(res[i]>0x3f3f3f3f)
        {
            cout<<"impossible";
            return 0;
        }
    }

     cout<<resmax;
}