题目内容：

输入一棵二叉树前序遍历和中序遍历的结果，请重建该二叉树。

注意:

二叉树中每个节点的值都互不相同；
输入的前序遍历和中序遍历一定合法；
数据范围
树中节点数量范围 $[0,100]$。

样例

给定：
前序遍历是：[3, 9, 20, 15, 7]
中序遍历是：[9, 3, 15, 20, 7]

返回：[3, 9, 20, null, null, 15, 7, null, null, null, null]
返回的二叉树如下所示：
    3
   / \
  9  20
    /  \
   15   7

这道题其实就是给定二叉树的前序和后序遍历，还原整棵二叉树。

那么给定我们二叉树的前序和后序遍历，该怎么还原整棵二叉树呢？

先来看一下样例。第一步先找到整棵树的根节点，就是前序遍历中的第一个数，于是我们把它画上去。

然后在中序遍历中找到$3$，左边的$9$就是它的左子树，右边的$15,20,7$就是它的右子树。
左子树只有$1$个$9$所以直接画上去，然后再处理右子树。

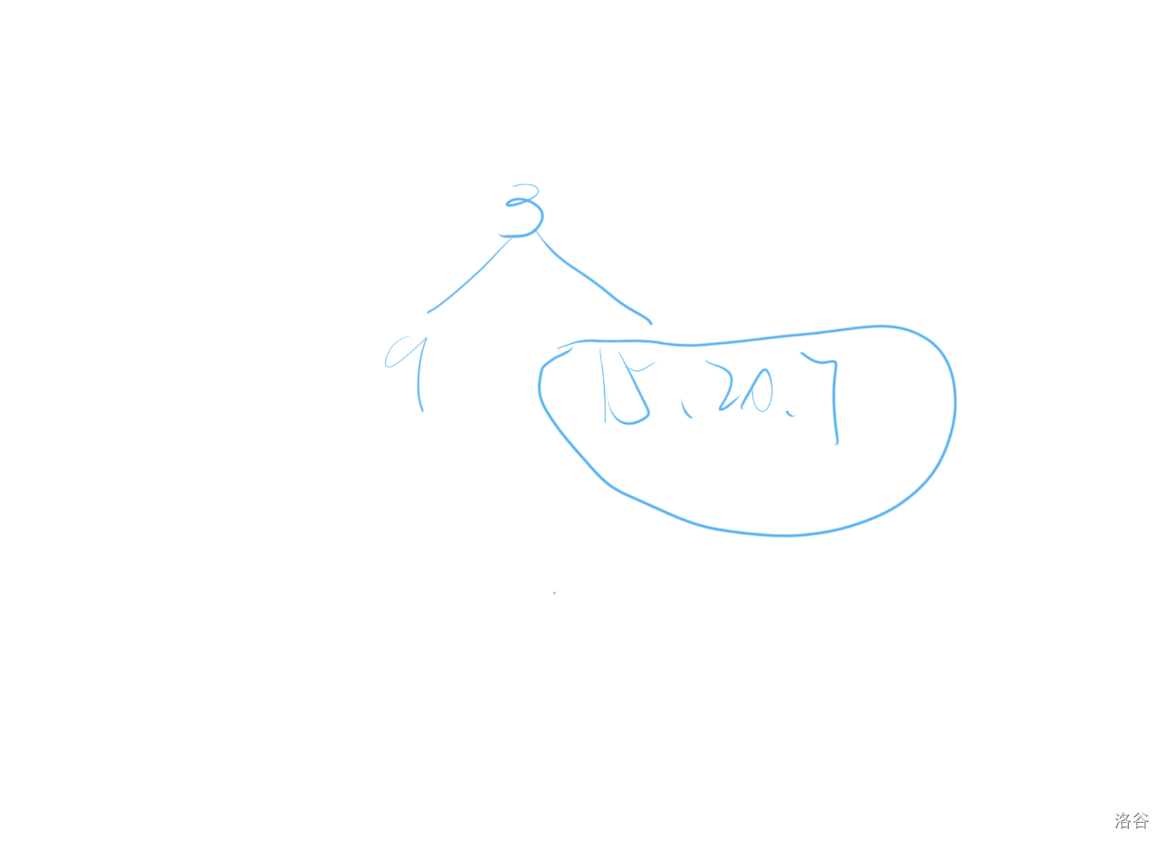
在前序遍历中找到左子树$9$的位置，下一个数就是右子树的根节点，再把$20$画上去。

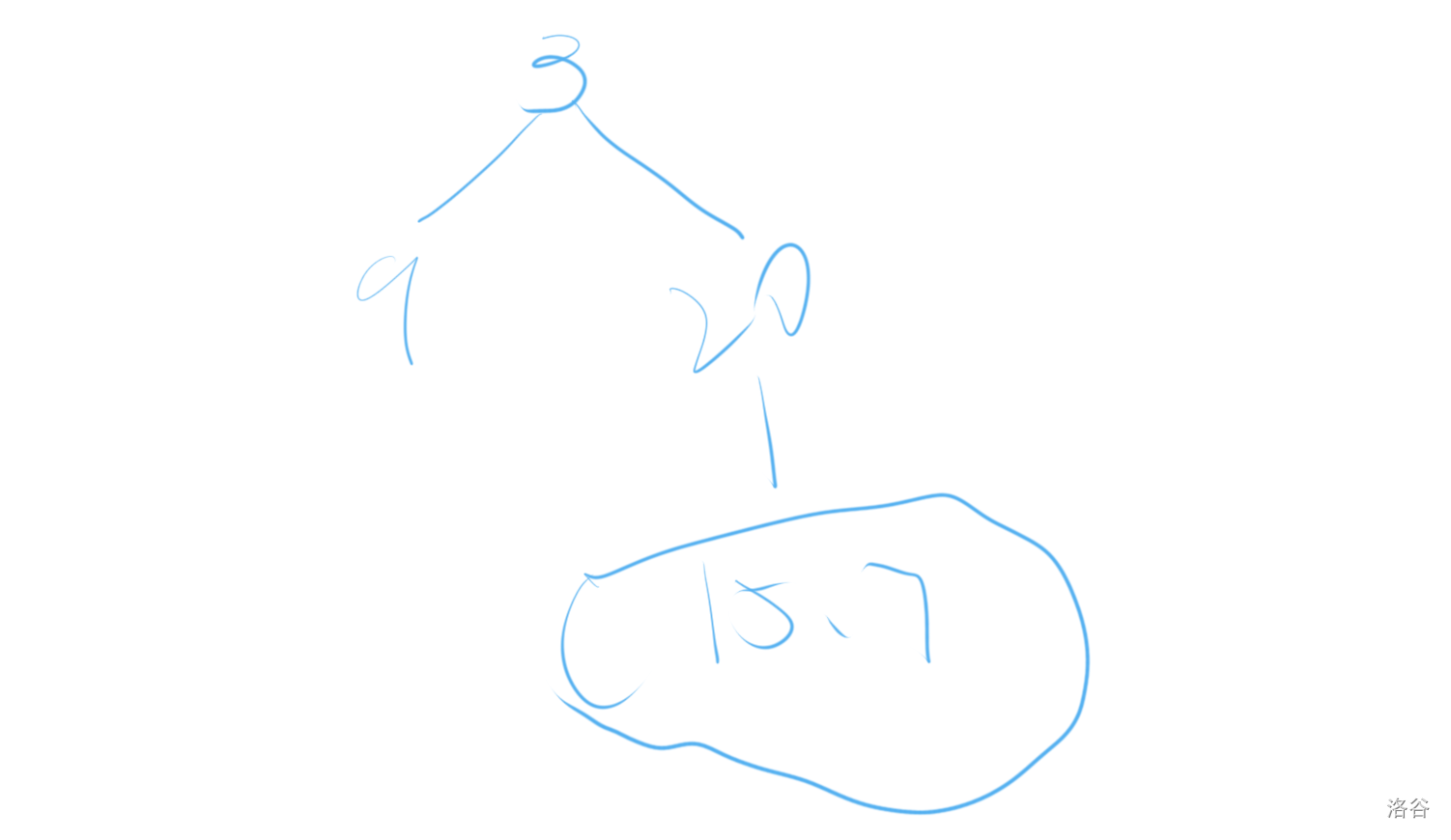
再在中序遍历中找到$20$，排除已经画过的$3,9$，$20$的左子树就是$15$，右子树就是$7$。

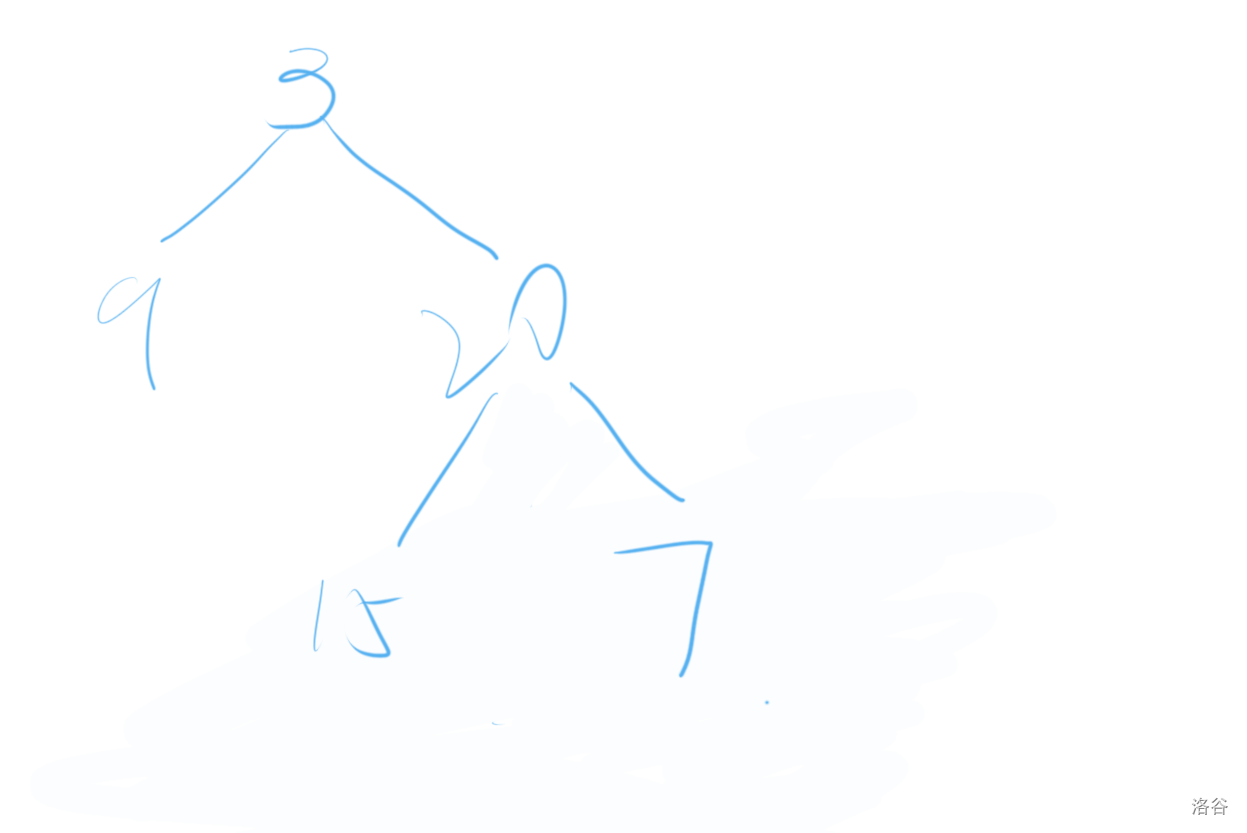
所以思路就是根据前序排列找到根节点，再在中序排列中找出左右子树，最后递归处理左右子树。

终于来到了代码环节

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left；
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    map<int, int> pos;//记录中序排列中每个数值的下标

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int l = preorder.size();//先记录长度，方便处理，preorder与inorder的长度是一样的
        for (int i = 0; i < l; i ++)
            pos[inorder[i]] = i;
        return dfs(preorder, inorder, 0, l - 1, 0, l - 1);
    }

    TreeNode* dfs(vector<int> pre, vector<int> in, int pl, int pr, int il, int ir)
    {
        if (pl > pr) return NULL;//如果没有数就返回NULL
        int k = pos[pre[pl]] - il;//根节点再中序遍历中的位置
        TreeNode* root = new TreeNode(pre[pl]);
        //在中序遍历中找到根节点的位置 k，则 k 左边是左子树的中序遍历，右边是右子树的中序遍历
        //假设左子树的中序遍历的长度是ll，则在前序遍历中，根节点后面的l个数，是左子树的前序遍历，剩下的数是
        //右子树的前序遍历
        root->left = dfs(pre, in, pl + 1, pl + k, il, il + k - 1);//递归处理左子树
        root->right = dfs(pre, in, pl + k + 1, pr, il + k + 1, ir);//递归处理右子树
        return root;
    }
};

谢谢你看到这里，既然都看到最后了，如果喜欢，不妨给可爱的男孩子一个赞呗，觉得有问题也可以在评论区指出来哦！

感谢观看！！！

$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\mathcal{writer\enspace by \enspace acwing}$ : $\mathfrak{天元之弈}$