$$\color{red}{算法}\color{blue}{基础课}\color{purple}{笔记and题解}\color{green}{汇总}$$

笔记：
给定模板串$P$和模式串$S$。
要求在$S$中查找$P$。

问题关键在于处理“失配”。

我们引入一个数组$nxt$，表示：
若$nxt_i=j$，那么$P[1,j]=P[i-j+1,i]$，$nxt_i=max_j$。
也就是“$P$中以$i$结尾的非前缀字串”与“$P$的前缀”所能匹配的最长长度。
而我们在暴力算法中，肯定是每次把$P$整个往后移动一位，再进行比较。
然而我们对$P$自匹配出$nxt$的时候，就是查找$P$的“自相似性”，也就是自己中的循环节。
我们来看一张示意图。

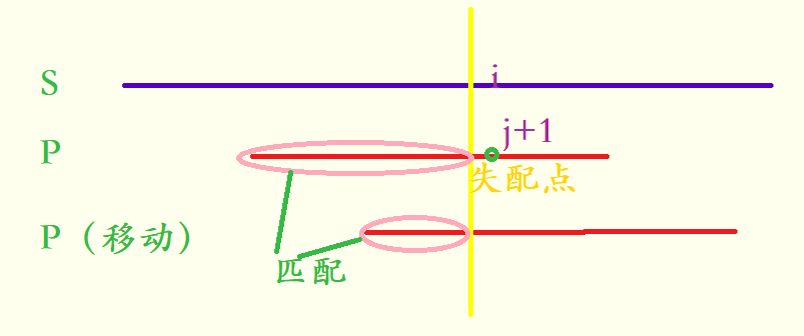
在上图中，$P$要移动了，但是我们发现没有必要把$P$往后移动一格，而应该直接跳到$nxt$的位置上，因为这样确保前一段是相同的，如果一位一位跳太“节省时间”了，数据范围稍大就会$TLE$。

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 1000010;
char p[N], s[M];
int n, m, nxt[N], f[N];
int main() {
    cin >> n >> p + 1 >> m >> s + 1;

    //求nxt的过程
    for (int i = 2, j = 0; i <= n; i++) {
        while (j && p[i] != p[j + 1]) j = nxt[j];
        if (p[i] == p[j + 1]) j++;
        nxt[i] = j;
    }

    //kmp匹配过程
    for (int i = 1, j = 0; i <= m; i++) {
        while (j && s[i] != p[j + 1]) j = nxt[j];
        if (s[i] == p[j + 1]) j++;
        if (j == n) {
            //匹配成功了
            printf("%d ", i - n);
            j = nxt[j];
        }
    }
    return 0;
}