算法分析

单调队列

顺时针

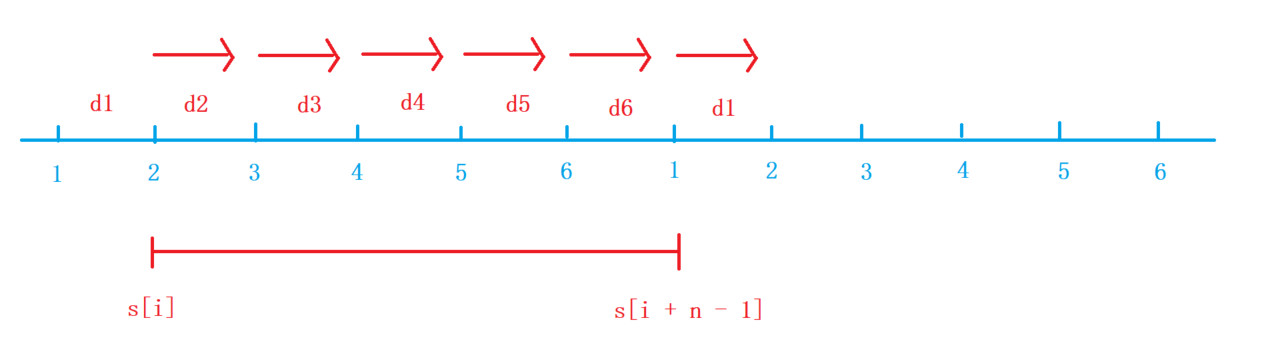
每个点i表示从i点加oil[i]的油再耗dist[i]的油所剩的油量,即oil[i] - dist[i]

• 1、计算出油量的前缀和
• 2、从某个点i出发，顺时针走一圈，在过程中油量始终 >= 0，等价于在[i,i + n - 1]中，对任意的j,i <= j <= i + n - 1，均有s[j] - s[i - 1] >= 0，即i固定，找s[j]的最小值，即从[i,i + n - 1]中找到滑动窗口的最小值
• 3、由于2操作，需要对i进行反向遍历，即从n * 2遍历到1，又由于i <= j <= i + n - 1，遍历到i时需要用到i位置的值，因此找[i,i + n - 1]区间最小值时需要在while后面的语句找

逆时针

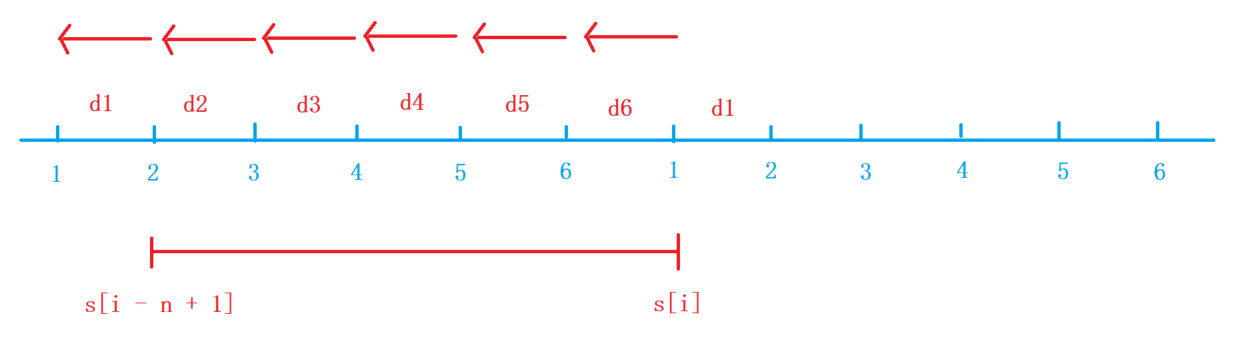
每个点i表示从i点加oil[i]的油再耗dist[i - 1]的油所剩的油量,即oil[i] - dist[i - 1]，其中1号点浩的是dist[n]的油，因此需要初始化dist[0] = dist[n]

• 1、计算出油量的后缀和
• 2、从某个点i出发，逆时针走一圈，在过程中油量始终 >= 0，等价于在[i - n + 1,i]中，对任意的j,i - n + 1 <= j <= i，均有s[j] - s[i + 1] >= 0，即i固定，找s[j]的最小值，即从[i - n + 1,i]中找到滑动窗口的最小值
• 3、由于2操作，需要对i进行正向遍历，即从1遍历到n * 2，又由于i - n + 1 <= j <= i，遍历到i时需要用到i位置的值，因此找[i - n + 1,i]区间最小值时需要在while后面的语句找

时间复杂度 $O(n)$

参考文献

算法提高课

Java 代码

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;

public class Main {
    static int N = 100000 * 2 + 10;
    static int[] oil = new int[N];
    static int[] dist = new int[N];
    static long[] s = new long[N];
    static int[] q = new int[N];
    static boolean[] st = new boolean[N];//表示从i点出发是否有解
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter log = new BufferedWriter(new OutputStreamWriter(System.out));
        int n = Integer.parseInt(br.readLine());
        for(int i = 1;i <= n;i ++)
        {
            String[] s1 = br.readLine().split(" ");
            oil[i] = Integer.parseInt(s1[0]);
            dist[i] = Integer.parseInt(s1[1]);
        }
        //顺时针
        for(int i = 1;i <= n ;i ++) s[i] = s[i + n] = oil[i] - dist[i];
        for(int i = 1;i <= n * 2;i ++) s[i] += s[i - 1];
        int hh = 0,tt = -1;
        for(int i = n * 2;i >= 1;i --)
        {
            if(hh <= tt && q[hh] > i + n - 1) hh ++;
            while(hh <= tt && s[q[tt]] >= s[i]) tt --;
            q[++ tt] = i;

            if(i <= n && s[q[hh]] - s[i - 1] >= 0) st[i] = true;
        }

        //逆时针
        dist[0] = dist[n];
        for(int i = n;i >= 1;i --) s[i] = s[i + n] = oil[i] - dist[i - 1];
        for(int i = n * 2;i >= 1;i --) s[i] += s[i + 1];
        hh = 0;
        tt = -1;
        for(int i = 1;i <= n * 2;i ++)
        {
            if(hh <= tt && q[hh] < i - n + 1) hh ++;
            while(hh <= tt && s[q[tt]] >= s[i]) tt --;
            q[++ tt] = i;

            if(i >= n + 1 && s[q[hh]] - s[i + 1] >= 0) st[i - n] = true;
        }

        for(int i = 1;i <= n;i ++)
        {
            if(st[i]) log.write("TAK\n");
            else log.write("NIE\n");
        }
        log.flush();
    }
}