题目描述

给定两个正整数（不含前导 $0$），计算它们的和。

输入格式

共两行，每行包含一个整数。

输出格式

共一行，包含所求的和。

数据范围

$1≤整数长度≤100000$

输入样例：

12
23

输出样例：

35

算法1

(高精度) $O(n^2)$

这道题的整数长度是$≤100000$的，非常大，所以要用高精度来做。
那先来看这样一个算式。

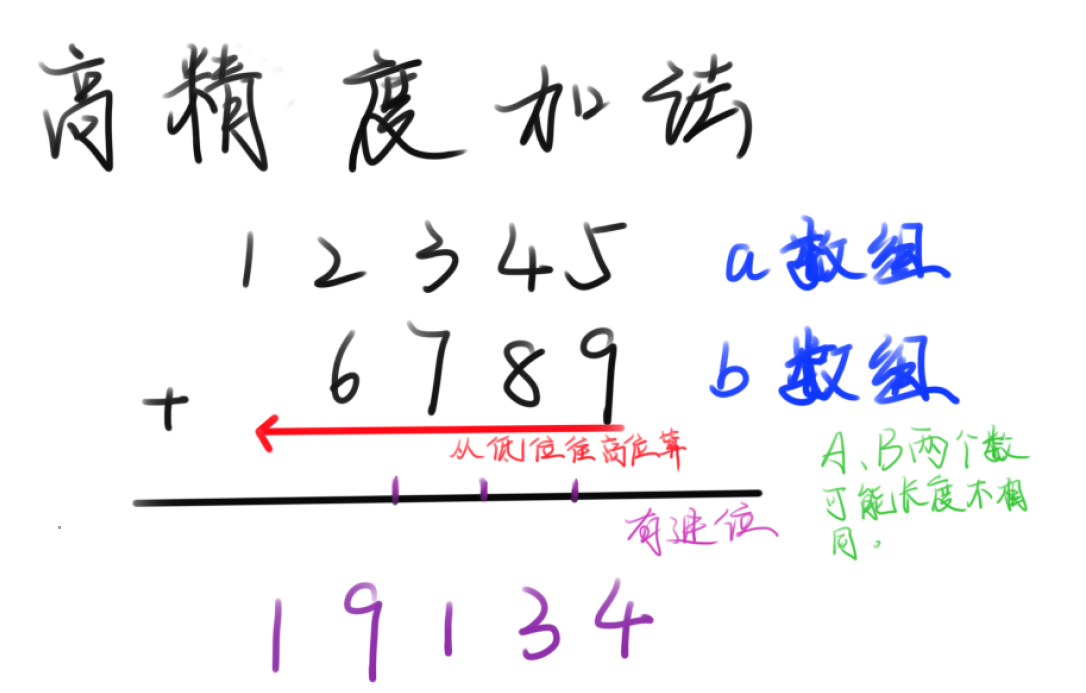
那观察这个算式，我们发现这个算式有以下特点：

• 从低位往高位算
• 有进位
• A、B两个数长度可能不同

这就是算式的特点，也是模拟这样一个算式的难点。

那我们来解决上面的这些问题

• 要从低位往高位算，那我们可以将这个数倒序，这样就可以从低位往高位算了
• 如果有进位，那我们就需要一个变量来存当前位置上加起来有多少，当前这个位上就是这个数$% \ 10$（因为这是十进制，逢十进一），然后把这个变量整除$10$就行了。
• A、B两个数长度可能不同，那我们在每一个位上要相加时，如果当前遍历到的长度小于a的长度，那就把这个变量加上当前位上的数，同理，如果当前遍历到的长度小于b的长度，那就把这个变量加上当前位上的数，这样就可以解决这个问题

时间复杂度

参考文献

C++ 代码（无注释代码见高精度加法）

$\ STL$版本

#include <iostream>
#include <vector>
using namespace std;
/* A + B */
vector <int> add(vector <int> &A,vector <int> &B){ // &是取地址符，如果没有，计算机只会拷贝一个数组，加上就直接在A和B上操作了，去掉也可以，因为这道题目没有要输出A和B最后变成什么了
    vector <int> C; // 最终答案
    int t = 0; // 当前位置上的和
    for(int i = 0;i < A.size() || i < B.size();i ++){ // 遍历一遍A和B数组，直到两个数组都遍历完为止
        if(i < A.size()) t += A[i]; // 如果没有遍历完A数组，t加上a当前位上的值
        if(i < B.size()) t += B[i]; // 如果没有遍历完A数组，t加上a当前位上的值
        C.push_back(t % 10); // 因为有可能进位，所以要push上的是t % 10
        t /= 10; // 如果t大于10，也就是进过位了，所以要/ 10
    }
    if(t) C.push_back(1); // 如果最高位还要进1，进1
    return C; // 返回C，也就是最终答案
}
int main(){
    string a,b; // a和b，需要相加的两个很大的数。因为可能很大，所以a和b要用string类型，而且也方便计算这个数的长度
    vector <int> A,B; // 用vector倒序更好做
    cin>>a>>b; // 读入，注意这里用scanf的话string类型会把换行读进去。
    for(int i = a.size() - 1;i >= 0;i --) A.push_back(a[i] - '0'); // 把a倒序
    for(int i = b.size() - 1;i >= 0;i --) B.push_back(b[i] - '0'); // 把b倒序
    auto C = add(A,B); // C为A + B的结果，auto是让计算机自己猜测这是什么类型，在这里表示vector <int>
    for(int i = C.size() - 1;i >= 0;i --) printf("%d",C[i]); // 倒序输出C，因为A + B的结果是倒着的
    return 0;
}

数组版本

（自认为还是挺短的）

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100010;
string stra,strb;
int lena,lenb,lenc;
int a[N],b[N];
int c[N];
void add(int a[],int b[]){ 
    int t = 0; // 进位
    lenc = max(lena,lenb); // 求出最大的长度
    for(int i = 1;i <= lenc;i ++){ // 计算
        t += a[i] + b[i]; // 算出一位相加的和
        c[i] = t % 10; // 将余下的结果存入c
        t /= 10; // 计算出进位
    }
    if(t) c[++ lenc] = 1; // 如果进位超出a和b的最大长度，进位，将新的一位设为1
}
int main(){
    cin.tie(0);
    cin>>stra>>strb; // 读入两个数
    lena = stra.size(),lenb = strb.size(); // 记录下两个数的长度
    for(int i = 1;i <= lena;i ++) a[i] = stra[lena - i] - '0'; // 将字符串stra和strb倒过来存入数组a，b
    for(int i = 1;i <= lenb;i ++) b[i] = strb[lenb - i] - '0';
    add(a,b); // 高精度加法函数
    for(int i = lenc;i >= 1;i --) printf("%d",c[i]); // 倒序输出（原因是为了方便计算，把a和b倒了过来，所以c数组中的数字也是倒序的）
    return 0;
}

当然，我们可以压位。

所谓压位，就是指充分利用 $a$ 数组的空间，我们将多位数字存入同一个位中。

高精度加法压位的极限是 $9$ 位数字。

#include <iostream>
#include <vector>
using namespace std;
auto add(auto A,auto B){
    int t = 0;
    vector <int> C;
    for(int i = 0;i < A.size() || i < B.size() || t;i ++){
        if(i < A.size()) t += A[i];
        if(i < B.size()) t += B[i];
        C.push_back(t % 1000000000); // 我们存了9位，在进位时自然要模上10^9
        t /= 1000000000;
    }
    return C;
}
int main(){
    string a,b;
    cin>>a>>b;
    vector <int> A,B;
    int t = 1,j = 0,s = 0; // t 为加入一位需要乘的数字 ，j为当前压入了多少位数字（到9位后停止），s为每一位的数字（最多有9位）
    for(int i = a.size() - 1;i >= 0;i --){
        s += (a[i] - '0') * t;
        t *= 10;
        j ++;
        if(j == 9 || i == 0){
            A.push_back(s);
            s = 0;
            j = 0;
            t = 1; // 新压入一位，重新开始
        }
    }
    s = 0; // 处理 B
    j = 0;
    t = 1;
    for(int i = b.size() - 1;i >= 0;i --){
        s += (b[i] - '0') * t;
        t *= 10;
        j ++;
        if(j == 9 || i == 0){
            B.push_back(s);
            s = 0;
            j = 0;
            t = 1;
        }
    }
    auto C = add(A,B);
    printf("%d",C.back());
    for(int i = C.size() - 2;i >= 0;i --) printf("%09d",C[i]);
    return 0;
}

之后你会发现时间快了 $20ms$ 左右，因为压位后直接 $9$ 位 $9$ 位地开始计算，免去 $1$ 位 $1$ 位算的时间。

struct 数组模拟版本

这里提供一个比较有用的写法。

运用 $struct$ 写出结构体，操作简单，可以很容易地实现高精度加法。

主要是封装在结构体中看起来比较美观。

在前面做法给出我打卡链接的地方也有此份无注释代码。（顶端）

当然最主要的是发现爆 $long$ $long$后可以比较简单的改正。（不需要重构代码）

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 1e5 + 10;
struct bignum{
    char s[N]; // 读入进的超大数字。
    int a[N],len; // 存储每一位的数字，以及整个数字的位数。
    bool flag; // 判断是否需要加负号，当然不需要考虑负号情况。
    bignum(){ // 无参构造，初始化长度 1，数字数组全部为 0，且非负。
        memset(a,0,sizeof a);
        len = 1;
        flag = 0;
    }
    bignum(int x){ // 如果读入的是数字（int 类型），将其存入 a 数组中
        while(x){
            a[len] = x % 10;
            x /= 10;
            len ++;
        }
        len --;
    }
    int &operator [] (int i){ // 重载 [] ，使访问数组中内容更加方便（因为这是结构体，无法确定你想要的是哪一个数字）
        return a[i];
    }
    friend bool operator < (bignum a,bignum b){ // 重载 <，判断 a 是否小于 b。
        if(a.len < b.len) return true;
        if(a.len > b.len) return false;
        for(int i = a.len;i >= 1;i --){
            if(a[i] < b[i]) return true;
            if(a[i] > b[i]) return false;
        }
        return false;
    }
    friend bool operator > (bignum a,bignum b){ // 重载 >，判断 a 是否大于 b。
        if(a.len < b.len) return false;
        if(a.len > b.len) return true;
        for(int i = a.len;i >= 1;i --){
            if(a[i] < b[i]) return false;
            if(a[i] > b[i]) return true;
        }
        return true;
    }
    friend bool operator == (bignum a,bignum b){ // 重载 ==，判断 a 是否等于 b。
        if(a.len != b.len) return false;
        for(int i = a.len;i >= 1;i --){
            if(a[i] != b[i]) return false;
        }
        return true;
    }
    void input(){ // 输入
        scanf("%s",s + 1);
        len = strlen(s + 1);
        for(int i = 1;i <= len;i ++) a[i] = s[len - i + 1] - '0';
    }
    void print(){ // 输出
        if(flag) printf("-");
        for(int i = len;i >= 1;i --) printf("%d",a[i]);
    }
};
bignum operator + (bignum a,bignum b){ // 重载 +，高精度加法，实现方法与上面的数组模拟方法相同，不再赘述。
    bignum c;
    c.len = max(a.len,b.len);
    long long t = 0;
    for(int i = 1;i <= c.len;i ++){
        t += a[i] + b[i];
        c[i] = t % 10;
        t /= 10;
    }
    if(t){
        c.len ++;
        c[c.len] = 1;
    }
    return c;
}
int main(){
    bignum a,b,c; // 简单的 a + b，我甚至拿来交了一下 A+B（
    a.input();
    b.input();
    c = a + b;
    c.print();
    return 0;
}