Question

There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list piles, where piles[i] is a list of integers denoting the composition of the ith pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.

Eaxmples:

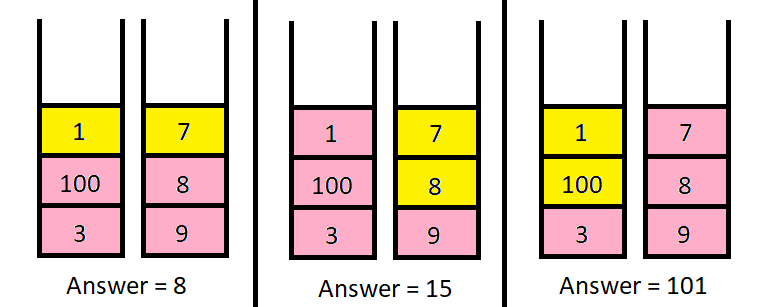
Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
Explanation:
The maximum total can be obtained if we choose all coins from the last pile.

Constraints:

n == piles.length
1 <= n <= 1000
1 <= piles[i][j] <= 105
1 <= k <= sum(piles[i].length) <= 2000

method1

(DP) $O(ks)$

$f[i][j]$ represents we choose from pile $1$ to pile $i$, and totally we have $j$ coins.

we can enumerate how many coins t we take at pile $i$, then the state tranferring equation will be:

$f[i][j]=max(f[i][j], f[i-1][j-t]+s[i][t]);$ $j$ should be less than $k$ and current total coins.

$t$ should be less than $j$ and ith day’s coins number.

C++ Code

class Solution {
public:
    int maxValueOfCoins(vector<vector<int>>& piles, int k) {
        int n=piles.size();
        vector<int>f(k+1);//select from 1-i, totally j times
        int res=0;

        vector<vector<int>>s(n+1);
        vector<int>sum_len(n+1);
        for(int i=1;i<=n;i++)
        {
            int m=piles[i-1].size();
            s[i]=vector<int>(m+1);
            for(int j=1;j<=m;j++)
                s[i][j]=s[i][j-1]+piles[i-1][j-1];
            sum_len[i]=sum_len[i-1]+m;
        }

        for(int i=1;i<=n;i++)
        {
            for(int j=min(k,sum_len[i]);j>=0;j--)
            {
                for(int t=0;t<=min(j,(int)piles[i-1].size());t++)
                {
                    f[j]=max(f[j], f[j-t]+s[i][t]);
                }
                //cout<<i<<" "<<j<<" "<<f[i][j]<<endl;
            }
        }


        return f[k];

    }
};

method2

(knapsack) $O(ks)$ s is total number of coins

knapsack problem with many groups, in each group, we can divide the problem into two parts,

choose ith item or not.

C++ code

class Solution {
public:
    int maxValueOfCoins(vector<vector<int>>& piles, int k) {
        int n=piles.size();
        vector<int>f(k+1);
        int s=0;
        for(int i=1;i<=n;i++)
        {
            s+=piles[i-1].size();
            for(int j=min(k,s);j>=0;j--)
            {
                int w=0;
                for(int v=1;v<=min(j,(int)piles[i-1].size());v++)
                {
                    w+=piles[i-1][v-1];                
                    f[j]=max(f[j],f[j-v]+w);
                }                
            }
        }

        return f[k];
    }
};