回文子串的最大长度题解

朴素思路（枚举）

遍历每一个字符，以该字符为中心向两边查找，逐个比较判断，其时间复杂度为 $O(n ^ 2)$，很显然，会 $\text{TLE}$。

算法1（字符串哈希 + 二分）

观察回文串，我们可以发现回文串分为两类：

1. 奇回文串 $a[1 \sim n]$，长度 $n$ 为奇数，且 $a[1 \sim n / 2 + 1] = reverse(a[n / 2 + 1 \sim m])$，它的中心点是一个字符。其中 $reverse(a)$ 表示把字符串 $a$ 倒过来；
2. 偶回文串 $b[1 \sim n]$，长度 $n$ 为偶数，且 $b[1 \sim n / 2] = reverse(b[m / 2 + 1 \sim m])$，它的中心点事两个字符之间的夹缝。

我们需要一个正的字符串，还需要一个反的字符串，如果正字符串等于反的字符串，那么奇数回文串就长度 $\times 2 + 1$,偶数回文串就直接长度 $\times 2$ 即可。

我们这么做是因为要找回文串，也就是前缀与后缀相等，拆分为一个正的字符串和一个反的字符串会更好处理。

所以，我们可以预处理出前缀 $hash$ 值，类似地，我们倒着预处理，求出后缀 $hash$ 值，就可以 $O(1)$ 计算任意子串正着或倒着读的 $hash$ 值。

这道题目中，我们枚举回文子串的中心位置 $i$。看从这个位置出发向左右两侧最长可以扩展出多长的回文串。也就是说：

1. 求出一个最大的整数 $p$ 使得 $s[i - p \sim i] = reverse(s[i \sim i + p])$；
2. 求出一个最大的整数 $q$ 使得 $s[i - q \sim i - 1] = reverse(s[i \sim i + q - 1])$。

我们对 $p$ 和 $q$ 进行二分答案，在所有枚举过的回文子串长度中取 $\max$ 即是本题答案，时间复杂度 $O(n \log n)$。

这里有一个小技巧：在每个字符前面添加 #，比如 aba 就被扩充为 #a#b#a，遍历每个字符，尝试以所有字符为对称中心的回文串最大的长度可能是多少。注意：这样做，长度的 $\times 2$ 或 $\times 2 + 1$ 要省略。

比如第一个 a，最大回文串是 #a#，第二个 b，最大回文串是 a#b#a。可以发现，当回文串最左边字符是 # 时，实际回文串的长度就是填充后对称中心左边子串的长度，例如 #a#中对称中心 a 左边只有一个字符，回文串的长度就是 $1$；而当回文串最左边字符是字母时，实际回文串的长度就是填充后对称中心左边子串的长度加上 $1$，例如 a#b#a 中对称中心 b 左边有 $2$ 个字符，回文串的长度就是 $2 + 1 = 3$。

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;

#define ull unsigned long long
const int N = 2000010, P = 131;

char s[N];
ull h1[N], h2[N], p[N];

ull get(ull h[], ull l, ull r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main()
{
    int cnt = 0;
    while (scanf("%s", s + 1) && strcmp(s + 1, "END"))
    {
        int n = strlen(s + 1) * 2;
        for (int i = n; i; i -= 2)
        {
            s[i] = s[i / 2];
            s[i - 1] = 'z' + 1;
        }
        p[0] = 1;
        for (int i = 1, j = n; i <= n; i ++ , j -- )
        {
            h1[i] = h1[i - 1] * P + s[i] - 'a' + 1;
            h2[i] = h2[i - 1] * P + s[j] - 'a' + 1;
            p[i] = p[i - 1] * P;
        }
        ull ans = 0;
        for (int i = 1; i <= n; i ++ )
        {
            ull l = 0, r = min(i - 1, n - i);
            while (l < r)
            {
                ull mid = (l + r + 1) / 2;
                if (get(h1, i - mid, i - 1) != get(h2, n - (i + mid) + 1, n - i)) r = mid - 1;
                else l = mid;
            }
            if (s[i - l] <= 'z') ans = max(ans, l + 1);
            else ans = max(ans, l);
        }
        printf("Case %d: %d\n", ++ cnt, ans);
    }
    return 0;
}

算法2（字符串哈希优化）

我们考虑改进算法 $1$。

第一个需要改进的地方就是算法 $1$ 最后需要判断回文串最左边是不是字符。

为什么需要判断？这是因为字符串最右边没有填充字符导致的。

比如 aba 原先填充得到 #a#b#a，最长回文串是 a#b#a，之所以回文串最左边会是正常字符，是因为最右边没有与开头的填充字符匹配的 #。

我们把字符串左右两边都加上 #，对于 aba 而言，填充后得到 #a#b#a#，b 左边最大回文串长度为 $3$ 个字符，aba恰好是 $3$，如果是 #a#b#b#a#，中间的 # 左边有 $4$ 个字符，最长回文串长度 abba 长度同样是 $4$，如此，便不用在讨论回文串最左边的字符是什么了，因为，只要字符串中所有字符的左右两边都有填充字符，最长回文串的最左边必然都是填充字符。

第二个需要改进的地方是：算法 $1$ 的思路是对以第 $i$ 个字符为回文串中心，二分求出其最大回文串的长度后，再继续二分求以第 $i + 1$ 个字符为中心的最大回文串的长度，比较更新答案。

我们发现：一旦第以 $i$ 个字符为中心的最大回文串的长度为 $res$，则后面字符回文串长度若是小于 $res$ 则不会更新解。所以我们不用浪费时间去二分答案，可以从以上一个字符为中心求出的最大回文串长度的基础上，进行判断下一个字符是否可能成为最大回文串的对称中心。

因为每次判断的回文串长度都是非递减的，所以总的时间复杂度为 $O(n)$。

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;

#define ull unsigned long long
const int N = 2000010, P = 131;

char s[N];
ull h1[N], h2[N], p[N];

ull get(ull h[], ull l, ull r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main()
{
    int cnt = 0;
    while (scanf("%s", s + 1) && strcmp(s + 1, "END"))
    {
        int n = strlen(s + 1) * 2;
        for (int i = n; i; i -= 2)
        {
            s[i] = s[i / 2];
            s[i - 1] = 'z' + 1;
        }
        s[ ++ n] = 'z' + 1;
        p[0] = 1;
        for (int i = 1, j = n; i <= n; i ++ , j -- )
        {
            h1[i] = h1[i - 1] * P + s[i] - 'a' + 1;
            h2[i] = h2[i - 1] * P + s[j] - 'a' + 1;
            p[i] = p[i - 1] * P;
        }
        ull ans = 1;
        for (int i = 1; i <= n; i ++ )
        {
            ull r = min(i - 1, n - i);
            if (ans >= r || get(h1, i - ans, i - 1) != get(h2, n - (i + ans) + 1, n - i)) continue;
            while (ans <= r && get(h1, i - ans, i - 1) == get(h2, n - (i + ans) + 1, n - i)) ans ++ ;
            ans -- ;
        }
        printf("Case %d: %d\n", ++ cnt, ans);
    }
    return 0;
}

算法3（马拉车）

不同于算法 $1$ 和算法 $2$，我们试着优化朴素思路。

首先，和上面一样，我们在每个字符间插入 #。并且为了使得扩展的过程中，不产生一些边界问题，在两端分别插入 ^ 和 $（两个不可能在字符串中出现的字符）。这样向中心扩展的时候，如果判断两端字符是否相等，到了边界就一定会不相等，跳出循环。

我们思考如何优化朴素思路。

发现一个问题：在判断回文串的比对过程中，是否每次比对都是必要的呢？

以样例abcbabcbabcba为例。

当遍历到第 $5$ 个字符 a 时，向两边扩散来找回文串的长度，b = b, c = c, b = b, a = a，最后得到以第 $5$ 个字符 a 为对称中心的最长回文串是 abcbabcba。

接着，遍历到第六个字符 b，发现 a != c。

继续遍历到第 $7$ 个字符 c，发现 b = b, a = a, …。

现在来看重复对比可能还不太明显。我们是从左向右将每个字符依次选为对称中心再去判断最大回文串的。可以发现，以第 $5$ 个字符 a 为对称中心的最长回文串中，a 左边的字符串是 abcb，右边的字符串是 bcba，满足回文串的性质，彼此对称。

回忆下以第 $4$ 个字符 b 为对称中心时回文串的查找操作，发现 c != a，于是终止。

那么第 $3$ 个字符 c 为对称中心时回文串的查找操作呢？也就是 b = b, a = a。

在已经判断过的回文串 abcbabcba 中，在遍历到对称中心 a 右边字符时，以某字符为对称中心查找最大回文串的比对操作早在之前查找以该字符与 a 的对称字符为对称中心的查找时就已经比对过了。

我们用一个数组 $p$ 保存从中心扩展的最大个数，而它刚好也是去掉 # 的原字符串的总长度。

求原字符串下标

用 $p$ 的下标 $i$ 减去 $p_i$，再除以 $2$，就是原字符串的开头下标了。

如上图：例如我们找到 $p_i$ 的最大值为 $5$，也就是回文串的最大长度是 $5$ ，对应的下标是 $6$，所以原字符串的开头下标是 $(6 - 5)/ 2 = 0$ 。所以我们只需要返回原字符串的第 $0$ 到 第 $(5 - 1)$ 位就可以了。

求 $p_i$

这是整个算法的关键，它利用了“回文对称”这一性质。

先看图：

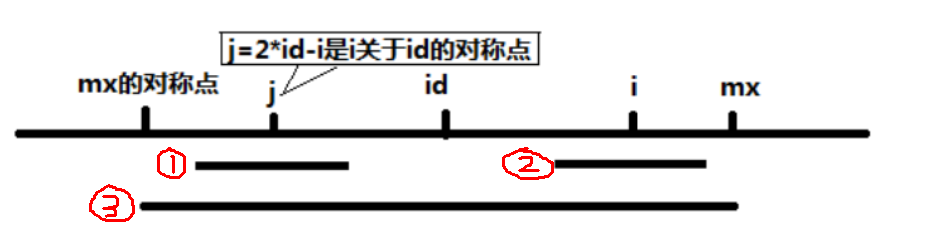
其中，我们一直在更新两个变量：

1. $id$：回文子串的中心位置
2. $mx$：回文子串的最后位置

再看公式：p[i] = min(mx-i, p[2 * id - i])

目前，我们知道了 $p[0 \sim i - 1]$ 的值，想要计算出 $p_i$。

上图中，①为以 $j$ 为中心的回文子串，②为以 $i$ 为中心的回文子串，③为以 $id$ 为中心的回文子串（首尾两端分别为 $mx$ 的对称点和 $mx$）。

那么，若是 $mx$ 在 $i$ 的右边，则咱们能够经过已经计算出的 $p_j$ 来计算 $p_i$，其中 $j$ 与 $i$ 的中心点为 $id$。

这里分三种情况：

1. 先直接令 $p_i$ 的回文子串就等于 $p_j$ 的回文子串，即②长度等于①，而后判断②的末尾是否超过了 $mx$，若是没有超过，则说明 $p_i$ 就等于 $p_j$。
   为什么？
   由于以 $id$ 为中心的回文子串为③，包含了①和②，并且①和②以 $id$ 为中心，那么必定有②=①。而且已经知道，①是以 $j$ 为中心的最长子串，那么②也确定是以 $i$ 为中心的最长子串。
2. 若是②的末尾超过了 $mx$，那么就只能让 $p_i = mx - i$ 了，我们能够保证至少半径到 $mx$ 这个位置，是能够回文的，可是一旦往右超出了 $mx$，就不能保证了，剩下的只能用朴素思路来获得最长回文子串。
3. 那若是②的左边超出了 $mx$ 的对称点，怎么办？不会出现这种状况的，由于①的右边不会超过 $mx$。若是超过了 $mx$，那么在上一次迭代中，$id$ 应该更新为 $j$，$mx$ 应该更新为 $j + p_j$。在迭代中，会始终保证 $mx$ 是全部已经获得的回文子串末端最靠右的位置。

另外，若是 $mx$ 不在 $i$ 的右边呢？那就利用不了③的对称性了，只能使用朴素算法慢慢算了。

最后

$ans$ 更新最大值即可。

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;

#define ull unsigned long long
const int N = 2000010, P = 131;

char s[N];
int p[N];

int main()
{
    int cnt = 0;
    while (scanf("%s", s + 1) && strcmp(s + 1, "END"))
    {
        int n = strlen(s + 1) * 2;
        for (int i = n; i; i -= 2)
        {
            s[i] = s[i / 2];
            s[i - 1] = 'z' + 1;
        }
        s[0] = '$';
        s[ ++ n] = 'z' + 1;
        int mx = 0, id = 0, ans = 0;
        memset(p, 0, sizeof p);
        for (int i = 1; i <= n; i ++ )
        {
            if (mx > i) p[i] = min(mx - i, p[2 * id - i]);
            else p[i] = 1;
            while (s[i - p[i]] == s[i + p[i]]) p[i] ++ ;
            if (p[i] + i > mx)
            {
                mx = p[i] + i;
                id = i;
            }
            ans = max(ans, p[i]);
        }
        printf("Case %d: %d\n", ++ cnt, ans - 1);
    }
    return 0;
}

在Acwing只算思路最长的一篇题解了（至少现在是），给个赞吧QwQ！