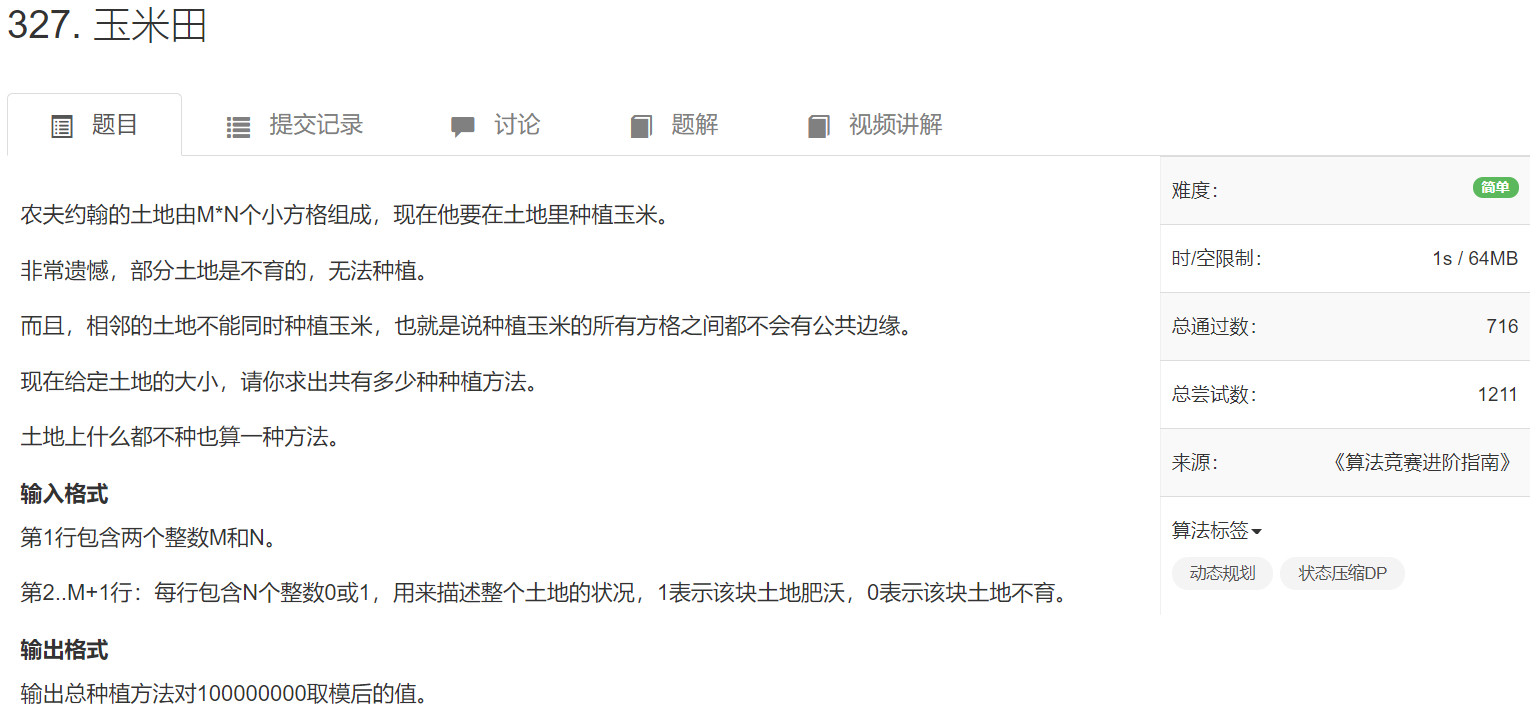
题目

输入输出

分析

考虑状态的表示通常需要保存一定的状态数据(一种状态需要对应一种数据值)
同时每个状态数据可以分解成许多数据单元

通常情况下每个状态数据可以通过一个整数来表示同时将这个整数分解成二进制形式。

比如在一行棋盘的格子上放棋子，在格子上放棋子表示1不放棋子表示0。

这样用0或者1来表示状态数据的每个单元，而整个状态数据就是一个一串0和1组成的二进制数。
通常这样的状态数据实现为一个基本的数据类型或者一种哈希值，同时需要注意的是状态数据中的每个单元不能太多。

具体这道题目的思路

状态转移方程
f[i][j]表示所有摆完前i行，且第i行状态为j的方案数
那么对于每一个合法的状态f[i][b]，上一行的状态为f[i-1][a];
那么f[i][b] += f[i-1][a]枚举每一个上一行能转移到下一行的状态
如果我们能枚举出每个能从i-1行状态转移到第i行的状态，然后把所有能转移的状态全部加起来并取模就得到了所有能转移到第i行的合法状态

状态压缩dp一般都要求预先把合法的状态i能够转移到其他所有合法状态都预先处理出来
注意，这里有两个要求，第一是状态合法，第二是状态i能够转移到状态j，那么我们就把能转移的合法状态记录下来
即head[state[i]].push_back(state[i]);

具体的步骤

1. 因为题目给的条件是1表示土地肥沃可以种，0表示不能种，这里我根据习惯把所有的1变成0，把所有的0变成1，即1代表不能种，0代表可以种，即a[i][j] ^= 1，这样做的好处是不能种的地方为1方便判断，比如上一层对应的状态与这一层对应状态的同一列都为1的话说明状态i就不能转移到状态j，这个时候我们只用判断state[i] & state[j] 如果大于0的话说明不合法
   即

bool check(int a,int b)//检查a和b的两个状态是否有重合的部位,这里的a和b对应着二进制状态的十进制表示
{
    return !(a & b);
}

1. 然后把每一行的01序列转化为十进制存放到num数组里面

2. 枚举从0到(1 << m) - 1的合法状态并且存放到state中，这里的合法状态是指状态的二进制表示不能有连续的1

3. 枚举每一个合法的状态state，如果state[i]和state[j]没有重合的1的话说明状态可以由state[j]转移到state[i]
   并且存放到head[M]中，即head[state[i]].push_back(state[j])

4. 初始化f[0][0] = 1,表示一行都没摆的情况下，方案数为1
   然后枚举每一行i从1到n
   令c = num[i]表示第i行初始的状态
   然后再枚举合法的状态，如果第i行初始的状态与合法的状态state[j]没有重复的1的时候
   表示第i行可以种成state[j]的形式
   然后再枚举能转移到state[j]的每个状态，表示上一层能够转移到下一层的所有可能的合法状态，最后加上取模

if(check(c,state[j]))
  {
    for(int k : head[state[j]])
       {
         f[i][state[j]] = (f[i][state[j]] + f[i-1][k]) % mod;
       } 
  }

再次强调一下，因为我这里把题目中的0和1全部都颠倒了一遍，即0变成1,1变成0，这样做的好处就是如果判断冲突的时候同一列位置如果都是1就不能种下去，方便我们判断

最后的结果就是第n行枚举每个状态i从1到 (1 << m) -1
res = (res + f[n][i]) % mod
如果能转移到的状态就存在对应的值，不能转移到的状态对应的值就为0

当然你也可以跟y总那样枚举到n+1行，然后f[n+1][0]就是对应的最终值

代码如下

#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>

using namespace std;

const int N = 15,M = 1 << 12,mod = 100000000;

int f[N][M];//f[i][j]表示所有摆完前i行，且第i行状态为j的方案数
int a[N][N];//记录初始的地图
int num[M];//记录每一行初始的二进制状态的十进制表示
int n,m;
vector<int>state;//记录合法的状态
vector<int>head[M];//head[state[i]]表示能转移到state[i]的所有合法状态

int calculate(vector<int> t)//把每一层的二进制状态转换成十进制
{
    int res = 0;
    reverse(t.begin(),t.end());//把二进制翻转一下方便我们计算
    for(int i = 0;i < t.size();i++)
    {
        res += pow(2,i)*t[i];
    }
    return res;
}

bool judge(int t)//如果哪个状态有连续的1说明不能作为合法的状态
{
    for(int i = 0;i < m;i++)
    {
        if((t >> i & 1) && (t >> (i+1) & 1)) return false;
    }
    return true;
}

bool check(int a,int b)//检查a和b的两个状态是否有重合的部位
{
    return !(a & b);
}
/*
//等价写法
bool check(int a,int b)//检查a和b的两个状态是否有重合的部位
{
    for(int i = 0;i < m;i++)
    {
        if((a >> i & 1) && (b >> i & 1)) return false;
    }
    return true;

}
*/
int main()
{
    cin>>n>>m;
    for(int i = 1;i <= n;i++)
    {
        vector<int>tmp;
        for(int j = 1;j <= m;j++)
        {
            cin>>a[i][j];
            a[i][j] ^= 1;//把所有的1变成0，所有的0变成1方便我们后续的判断
            tmp.push_back(a[i][j]);
        }
        num[i] = calculate(tmp);//把每一层的二进制状态转化为十进制
    }

    for(int i = 0;i < 1 << m;i++)//保证每个状态都没有连续的1
    {
        if(judge(i))//如果每个对应的二进制中没有连续的1，说明可以作为合法的状态并记录
        {
            state.push_back(i);
        }
    }

    for(int i = 0;i < state.size();i++)//state[i]和state[j]没有重合的1的话说明状态可以由state[j]转移到state[i]，并存放到head[M]里面
    {
        for(int j = 0;j < state.size();j++)
        {
            if(check(state[i],state[j]))
            {
                head[state[i]].push_back(state[j]);
            }
        }
    }
    f[0][0] = 1;//表示一行都没摆的情况下，方案数为1
    for(int i = 1;i <= n;i++)
    {
        int c = num[i];//第i行初始的状态
        for(int j = 0;j < state.size();j++)
        {
            if(check(c,state[j]))//如果第i行初始的状态与合法的状态state[j]没有重复的1的时候，表示第i行可以种成state[j]的形式
            {
                for(int k : head[state[j]])
                {
                    f[i][state[j]] = (f[i][state[j]] + f[i-1][k]) % mod;//枚举能转移到state[j]的每个状态，并加上取模
                } 
            }
        }
    }
    int res = 0;
    for(int i = 0;i < 1 << m;i++) res = (res + f[n][i]) % mod;
    cout<<res;

    return 0;
}