写题解不易，可以的话请在左边点一个👍，谢谢啦
原题链接

关键词：反向建图，链式前向星，堆优化版迪杰斯特拉，带点权判断

step1:抽象建图（理清基本题意，先不考虑等级限制）

首先来回顾一下y总的虚拟源点建图的思路：

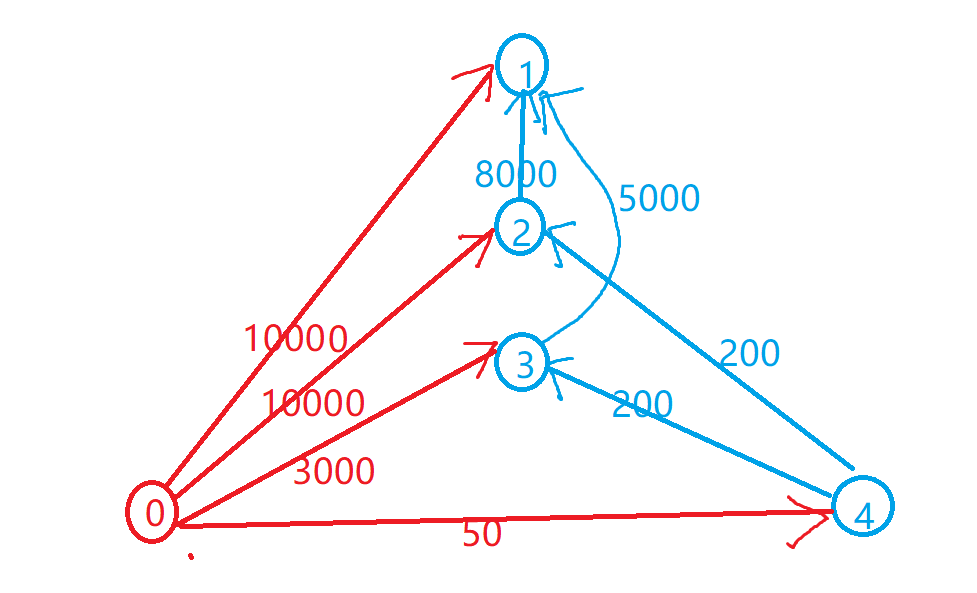
y总通过建立一个虚拟源点0，从0开始对每一个点进行建边，边的权值就是物品的价值，此时dist数组的含义就可以抽象为从0点出发，到达每一个点要购买的物品的最小花费。而我们最短路的终点则是酋长的允诺，因此，只需要求出dist[1] 即可

然后，事实上，我们可以这样抽象题意：我们最终可以直接从酋长的允诺出发作为起点,遍历全图，最后枚举每一个点，用到达该点的最短路+该点的物品价值更新答案，取最小值

这个很好理解，举题目中的意思来说，我们可以将酋长的允诺分解为8000的资金+皮袄（1000）或者5000的资金+水晶球（3000）。我们觉得皮袄还是太贵了，就继续向下分解让皮袄变成200的资金+4号物品（50）,此时为了得到1号物品（酋长的允诺），我们需要的是8200的资金+4号物品。以此类推对于每一种方案我们都可以将其分解为两部分：固定的资金+当前物品的价值。而这个固定的资金就是从国王的允诺（1号点）开始到达当前点的最短路径，我们迪杰斯特拉跑一遍最短路即可，最后在判断的时候，带上各点的权值即可。

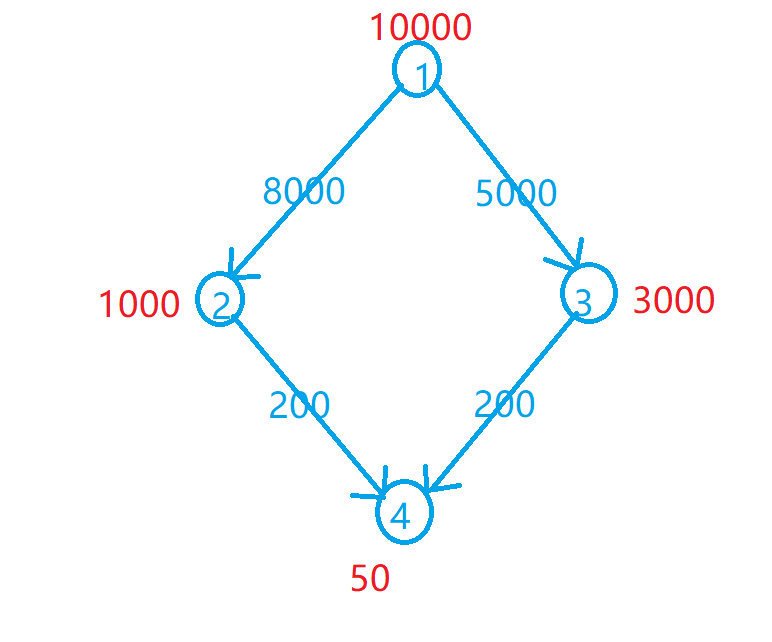
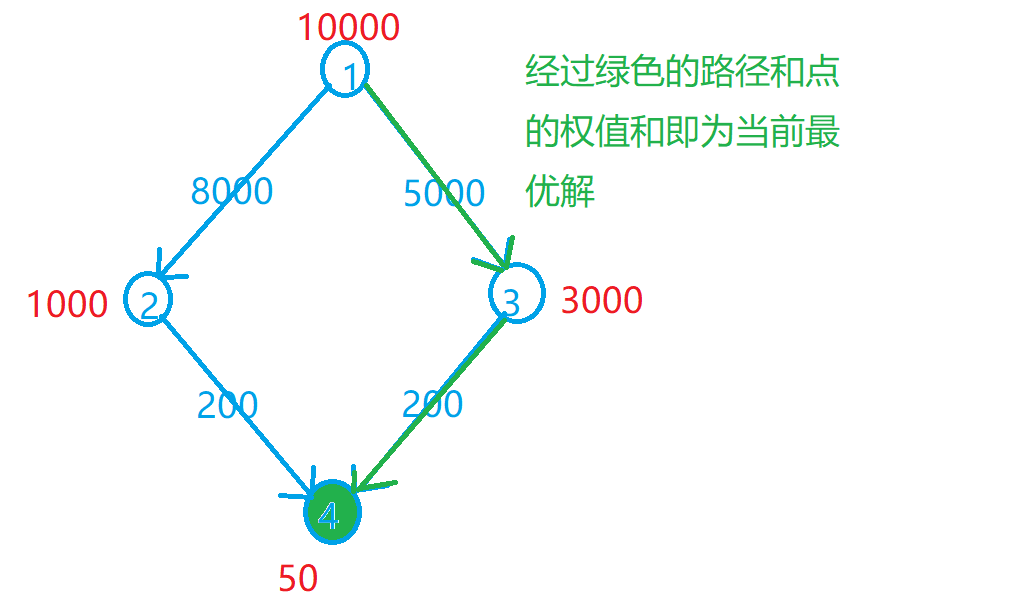
step2:关于等级限制（尝试枚举区间）

本题还有一个等级限制，每一个点都有对应的等级，两点间若跨等级超过限制，则不能交易。
而我们的最终目标是得到1号物品（酋长的允诺），所以我们可以枚举酋长的允诺所在的等级区间，在每一个等级区间里跑一遍迪杰斯特拉即可（在跑迪杰斯特拉时注意超过等级区间内的点不能入队），具体实现见代码

Q:为什么不能在跑迪杰斯特拉的时候直接将带权点入队，作为最短路的一部分。而是要在跑完一遍最短路以后再加上点权来更新当前最小值？

这个是这道题代码上最容易出错的地方，我debug了十几次才找出问题：dijkstra的本质就是用小的边来更新大的边所以如果每次更新时将点权带入就可能出现大边更新小边的情况这样就不能用dijkstra

step3:AC代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 150, M = 2e4;

int n, m;
int dist[N];
int Rank[N];  //代表每个编号对应的等级
int value[N]; //代表每个点的物品需要的钱
int h[N], ne[M], e[M], w[M], idx;
bool st[N];

void add(int a, int b, int c) //链式前向星建图
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int dijkstra(int l, int r)
{
    //以下是堆优化版迪杰斯特拉的模板
    memset(dist, 0x3f, sizeof dist);
    memset(st, 0, sizeof st); //由于要做多次迪杰斯特拉，所以务必记得每次初始化
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, 1});
    dist[1] = 0;
    while (heap.size())
    {
        int ver = heap.top().second;
        heap.pop();
        if (st[ver])
            continue;
        st[ver] = true;

        for (int i = h[ver]; ~i; i = ne[i])
        {
            int j = e[i];
            //在入队时多了一个条件判断当前点的等级是否在允许的范围内
            if (dist[j] > dist[ver] + w[i] && Rank[j] <= r && Rank[j] >= l)
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});
            }
        }
    }

    //在计算答案时，真实的答案值为到达该点的最短路径+该点的物品价值
    int res = 0x3f3f3f3f;
    for (int i = 1; i <= n; i++)
        res = min(res, dist[i] + value[i]);
    return res;
}

int main()
{
    cin >> m >> n;
    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> value[i] >> Rank[i] >> x;
        while (x--)
        {
            int b, c;
            cin >> b >> c;
            add(i, b, c); //反向建图，只能从高等级->低等级
        }
    }

    int res = 0x3f3f3f3f;
    //题意是有等级限制，因此需要枚举酋长所在的等级区间，每次用迪杰斯特拉跑一遍最短路
    //最终求出的最小的值即为答案
    for (int i = Rank[1]; i <= Rank[1] + m; i++)
        res = min(res, dijkstra(i - m, i));
    cout << res;
    return 0;
}