题目描述
略
证明
首先, 从右下角回传可以等价为从左上角同时传两次。要想两个路径除了起点和终点之外没有交点,那么肯定有一条路径完全位于另一条的上方。
现在考虑路径有交点的情况:
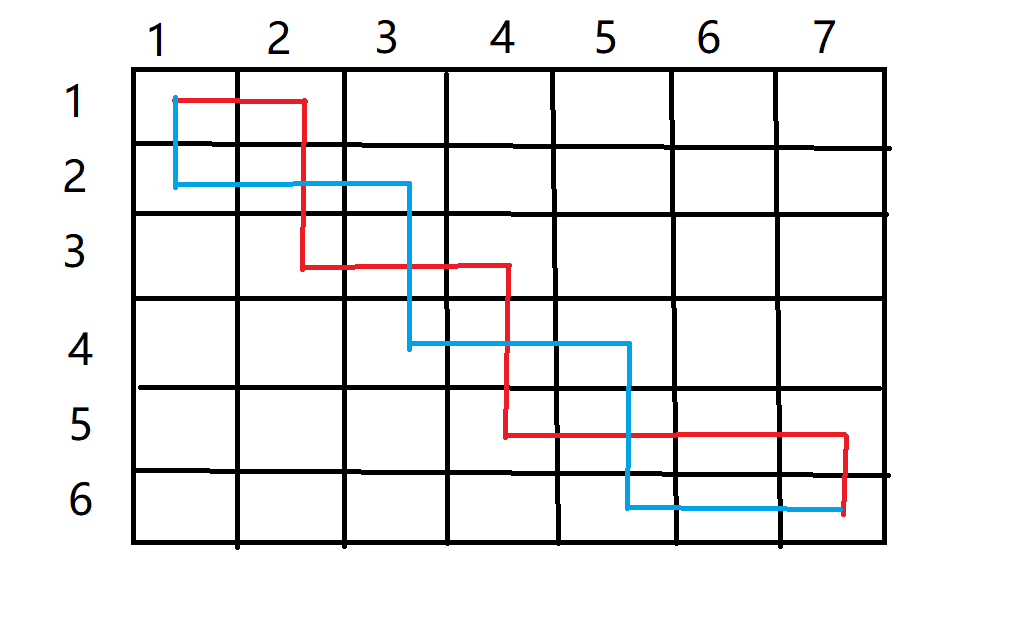
这种情况其实转换起来很简单,只要把位于红色线段上方的蓝色线段交换颜色就可以了,也就是说当红色处于蓝色的下方的时候,将红色的路径换成从蓝色的那段走是等效的(因为两条路径加起来经过的节点完全没有变)。
就可以得到:
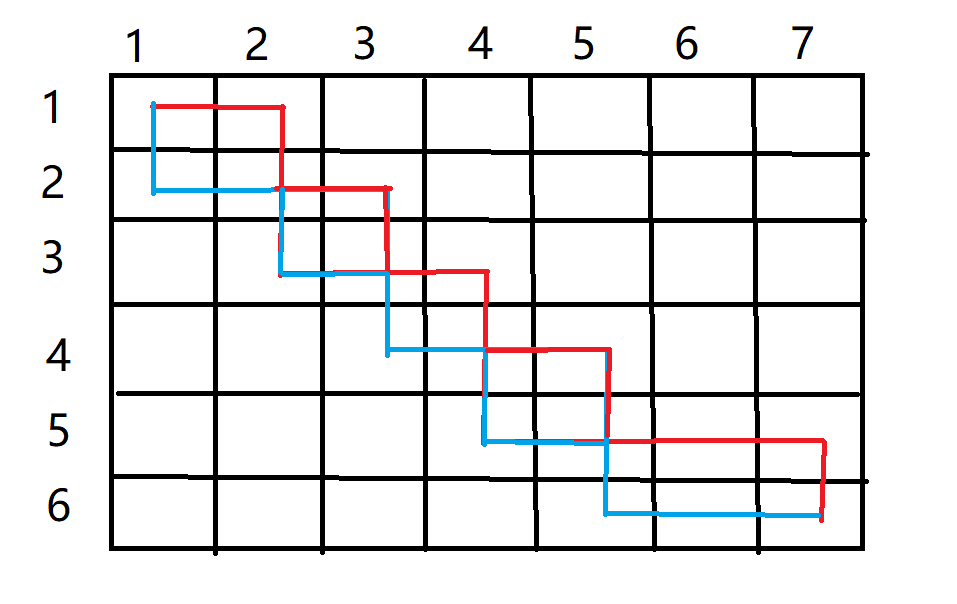
但是这个时候虽然满足了红色路径完全在蓝色的上方,但是却有交点。但是因为所有节点的权值都为非负数,那么可以证明这种情况永远不可能是最优解。比如以交点(2,2)为例,蓝色从(3,1)绕道或者红色从(1,3)处绕道一定不会比两条路径都从(2,2)处走差。
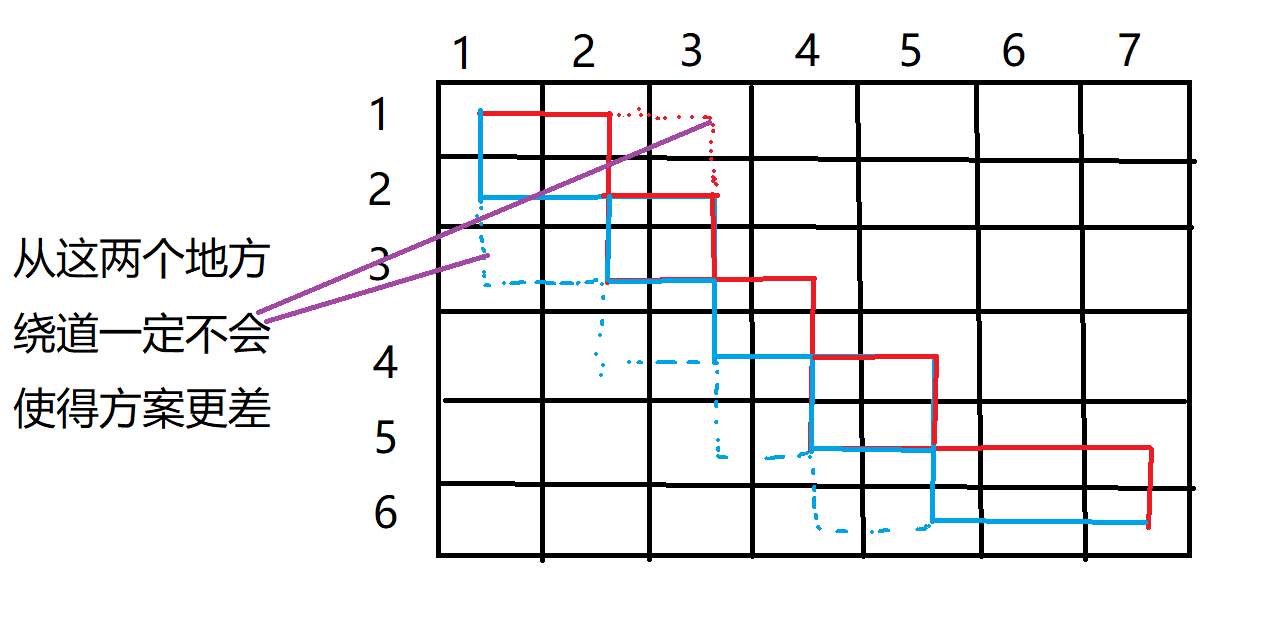
绕过交点之后,可以得到蓝色虚线的方案,该方案一定不会比之前的两个实线的方案更差。(当然该方案也不一定是最优的,还要确定应该由蓝色还是红色来走原来的交点的位置。
结论
不论是在 方格取数 中,还是在本题中,最优解永远不会由两段相交的路径组成。
那么代码中的相关位置的判断在事实上是起到了上述的确定是让蓝色还是红色走虚线的效果。
c++代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 55;
int mat[maxn][maxn];
int f[maxn<<1][maxn][maxn];
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&mat[i][j]);
for(int k=2;k<=n+m;k++){
for(int i=1;i<k;i++){
for(int j=1;j<k;j++){
int &v = f[k][i][j];
int tmp = mat[i][k-i];
if(i!=j){
tmp += mat[j][k-j];
}
v = max(f[k - 1][i - 1][j], v);
v = max(f[k - 1][i - 1][j - 1], v);
v = max(f[k - 1][i][j - 1], v);
v = max(f[k - 1][i][j], v);
v += tmp;
}
}
}
printf("%d\n",f[n+m][n][n]);
return 0;
}


因为两个点相交,这个点的值只能加一次,然而我们肯定能找到一条绕过这个点走到下个点的路径,这条路径一定是大于之前相交路径的,
数学表达就是:两条路径在一个点,那么在这个点加的值就是0+g[i,j] 但是我们可以让其中一条路径绕过这个点再走到这个点的下一个点 那么加的值应该是g[i,j-1] + g[i,j] 因为是非负数,所以我们可以找到一条大于等于之前有相交点的路径,那么这个有相交点的一定不是最优解;即便这条路径是最优解也有另一条最优解和这个路径和一样,但是我们只需要输出路径和就可以了,最优解路径有可能是有相交点的,但是也有另一个最优解没有相交点,那么我们输出的路径和肯定可以是一条没有相交点的最优解
👍
到这里看懂了
你这个解释醍醐灌顶👍
太绝杀了
tql
👍
这个解释好棒
好好好好好
%%%
补充一下,大家看题主的
图3对于路径有一点相交的情况,我们可以固定一个路径,比如蓝色固定,我们选择红色路径绕过相交的点,因为每个点的权值>=0,我们选择它绕过原先相交的点,此时蓝色还经过原先相交的点,那么红色路径绕过相交点之后,我们相当于多加了一个点的权值,最后加的总权值一定>=原先相交加一次点权值的情况,所以最优解等价于两条路径不想交
为什么只能加一次啊,我认为一次都不能加..因为要求不能重合,如果重合的话你只能发生在开头或者结尾。
口胡一下两道题的差别吧:
上一题是可以走相同的点,但是最优解一定不走相同的点。
这一题是不能走相同的点。
但是为什么要是
int t=w[i1][j2]; if(i1!=i2)t+=w[i2][j2];而非
t+=w[i1][就]+w[i2][j2]原因是: dp是一个递推的过程,这一步是构成最优的中间过程,是必须要的
我测,你这才是绝杀
我测,你这才是绝杀
我测,我被杀,构成最优的中间过程是什么意思啊 不懂啊
不懂啊,我原来还以为是点不相同所以就只加一次呢
就是即使最优解必然没有交点 但是没有交点的情况要由有交点的情况的值递推得出
绝杀!!!
天呐
意思是看似最优解只需要用到 t += w[i1][j1]+w[i2][j2]
实际上并非如此,它的前置状态需要
int t=w[i1][j2];
if(i1!=i2)t+=w[i2][j2];
前置状态正确,后面的状态才正确
简单讲就是相交或者不想交其实对于整个结果来说不影响
代码错了,数组越界了,i,j 越界了
大佬应该是无意,我还是想提醒下以免大家理解错了,其实在考虑先后顺序并且是dp解题的基础上。
从右下角回传不能等价为从左上角同时传两次。
如果先传出再传回:
因为纸条在传出的过程的结果一定是保证在传出过程中所有结果里最大的。
但此时的局部最优解保证不了能取到总体最优解。意思就是纸条传回过程中
由于先计算了传出过程中最大值而取不到总体的最大值了。(导致了本可以取到的最优总体而现在需要绕路
即需要违背题意行走)
这类问题应该都只能同时计算状态。而不能分先后。方格取数也是这样。感谢大佬分享思路
例如7*7的矩阵
0 0 2 3 0 0 0
0 0 3 0 0 0 0
0 0 3 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 4 0 0
0 0 0 0 4 0 0
0 0 2 0 4 0 0
坏了,被大佬整迷糊了。。所以是题目的问题吗,如果题目是先传出后传入那不就没有全局最优解了
可以等价
后面说的是对的
清晰,透彻!
就算两条路径有交叉,将两个连续十字交叉的中间部分做交换,多次进行,使得两条路径物理上交叉,而逻辑上是分开的
想问一下最后的输出 printf(“%d\n”,f[n+m][n][n]);
为什么不能是 printf(“%d\n”,f[n+m][n][m]);
因为f[k][i1][i2] 代表 : 走k步,两条路横坐标分别为i1和i2
f[k][n][m]代表第一条路横坐标走了为n,是不对的
对的,谢谢佬
xdm,想问一下
#include<iostream> using namespace std; const int N = 55; int w[N][N], f[N * 2][N][N]; int main() { int n, m; cin >> n >> m; for(int i = 1; i <= n; i ++) for(int j = 1; j <= m; j ++) cin >> w[i][j]; for(int k = 2; k <= n + m; k ++) for(int i1 = 1; i1 < k; i1 ++) for(int i2 = 1; i2 < k; i2 ++) { int j1 = k - i1, j2 = k - i2; if(j1 >= 1 && j1 <= m && j2 >= 1 && j2 <= m) { int t = w[i1][j1]; if(i1 != i2) t += w[i2][j2]; int &x = f[k][i1][i2]; x = max(x, f[k - 1][i1][i2] + t); x = max(x, f[k - 1][i1 - 1][i2 - 1] + t); x = max(x, f[k - 1][i1 - 1][i2] + t); x = max(x, f[k - 1][i1][i2 - 1] + t); } } cout << f[n + m][n][n] << endl; return 0; }这样运行没问题
但是把
int w[N][N], f[N * 2][N][N];改成
int f[N * 2][N][N], w[N][N];就会
SF
为什么呢
woc
为什么,我也想知道
请问找到原因了吗
还没呢
插眼
我猜测是代码里面的问题,因为你开的两个数组在内存里肯定是相邻的,换了位置却sf的话感觉是代码某个数组越界的问题
你把N开大一点就不会这样,我没仔细看你代码,但我猜测肯定是越界的问题,只不过换位置之前越界并没有被反馈出来
后面两个i的循环边界是小于等于n,不是小于k
插眼
for(int i1 = 1; i1 < k; i1 ++) for(int i2 = 1; i2 < k; i2 ++)i1<k和i2<k当k>55的时候不报SF才奇怪了
但是不换位置的时候能AC就神奇
输出了下数组的地址
//N=55 0x6011a0//f[0][0][0] 0x7460d4//f[N*2-1][N-1][N-1] 0x7460e0//w[0][0] 0x749020//w[N-1][N-1]这俩数组是挨一起的
访问到另一个数组就段错误了
应该是吧
对的 这个没特判i<=n
就是越界了,如果这样写 int f[N * 2][N][N], w[N][N]; 就要加上
for(int i1 = 1; i1 < k && i1 <= n ; i1 )
for(int i2 = 1; i2 < k&& i2 <= n; i2 )
就不报错了
我也遇到一样的问题了,给我整不会了
前提是都是非负数,方格取数严格来讲数据应该是带负数的,所以加入了一起走只算一次这个限制,可以用于两个路径一起走一段,避开负值
想了半天用dfs记忆化搜索,结果看到你这个贴子.....
博主,我有一点不明白,就是为什么for循环中i和j的范围是到k,而不是到n
天才证明
大哥!
如果直接过滤掉DP上一步相同的点,应该也能做到,且不用考虑正数限制。就是代码量会大一点。
为什么在for循环里面i<k和j<k哇,为什么不能设置小于n
orz!
提问: for(int k=2;k<=n+m;k)
{
for(int i1=1;i1<=n;i1)
{
for(int i2=1;i2<=n;i2)
{
这个样子是可以正常ac的,但如果换成 for(int k=2;k<=n+m;k)
{
for(int i1=1;i1<=k;i1)
{
for(int i2=1;i2<=k;i2)
{
就是wa为什么呢?
把等号去掉就是sf
厉害!
想问一个问题:
// 实现1 v = max(f[k - 1][i - 1][j], v); v = max(f[k - 1][i - 1][j - 1], v); v = max(f[k - 1][i][j - 1], v); v = max(f[k - 1][i][j], v); v += tmp; // 实现2 v = max(f[k - 1][i - 1][j - 1] + tmp, v) v = max(f[k - 1][i - 1][j] + tmp, v) v = max(f[k - 1][i][j - 1] + tmp, v) v = max(f[k - 1][i][j] + tmp, v)上述的实现1和实现2应该不等效吧。
比如:
v = 5 f[k - 1][i - 1][j - 1] = 4 f[k - 1][i - 1][j] = 3 f[k - 1][i][j - 1] = 2 f[k - 1][i][j] = 1 tmp = 2 这时,实现1 v = 7,实现2 v = 6为啥还能ac呢,不懂啊。跪求大佬解析。
想明白了,因为f[k][i][j]这时候还等于0,所以任意一个数都不会小于f[k][i][j]