题目描述

给你一个整数数组 nums 和一个整数 k ，请你返回 非空 子序列元素和的最大值，子序列需要满足：子序列中每两个 相邻 的整数 nums[i] 和 nums[j] ，它们在原数组中的下标 i 和 j 满足 i < j 且 j - i <= k 。

数组的子序列定义为：将数组中的若干个数字删除（可以删除 0 个数字），剩下的数字按照原本的顺序排布。

样例

输入：nums = [10,2,-10,5,20], k = 2
输出：37
解释：子序列为 [10, 2, 5, 20] 。

输入：nums = [-1,-2,-3], k = 1
输出：-1
解释：子序列必须是非空的，所以我们选择最大的数字。

输入：nums = [10,-2,-10,-5,20], k = 2
输出：23
解释：子序列为 [10, -2, -5, 20] 。

提示：

• 1 <= k <= nums.length <= 10^5
• -10^4 <= nums[i] <= 10^4

算法分析

单调队列 + dp

直接dp，如图所示，复杂度是$O(nk)$，对照数据范围，会超过10^8，会gg

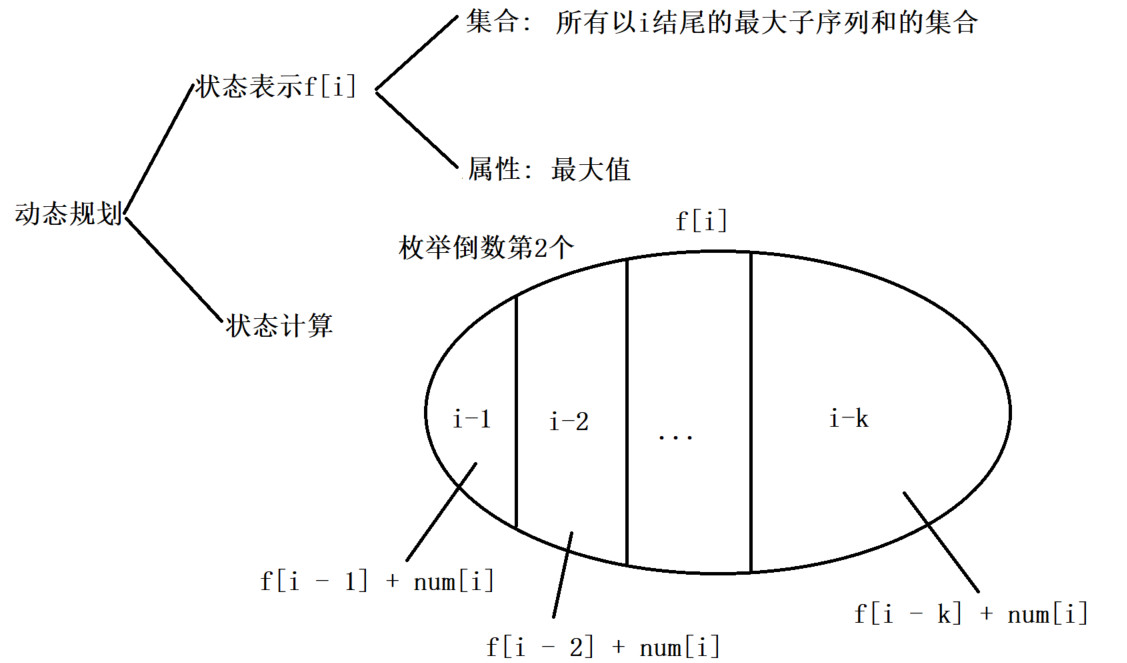
操作1：

滑动窗口大小是k

以i结尾的f[i]，滑动窗口的区间是[i - k,i - 1]，单调队列维护的是该区间的最小值，由于滑动窗口不包含i，因此f[i]需要在while上方进行更新

Java 代码

class Solution {
    static int N = 100010;
    static int[] f = new int[N];
    static int[] q = new int[N];
    public int constrainedSubsetSum(int[] nums, int k) {
        int n = nums.length;
        int hh = 0,tt = -1;
        int res = -0x3f3f3f3f;
        for(int i = 0; i < n;i ++)
        {
            f[i] = nums[i];
            if(hh <= tt && q[hh] < i - k) hh ++;
            if(hh <= tt) f[i] = Math.max(f[i],f[i] + f[q[hh]]);

            while(hh <= tt && f[q[tt]] <= f[i]) tt --;
            q[++ tt] = i;
            res = Math.max(res,f[i]);
        }
        return res;
    }
}

操作2：

• 1、由于枚举到i的时候，能转移的状态只有i - k到i - 1，固定是k个，因此求的是滑动窗口长度是k的最大值，用大根堆维护前k个状态的值，堆顶是最大值，从$O(k)$的复杂度变成了$O(logk)$的复杂度
• 2、若堆顶元素不是前k个状态，则直接poll出，循环该操作，f[i] 的转移方程是 f[i] = 堆顶 + num[i]，把当前位置(f[i],i)加入到大根堆中

时间复杂度 $O(nlogk)$

Java 代码

class Solution {
    PriorityQueue<Pair> q = new PriorityQueue<Pair>((x,y) -> y.val - x.val);
    public int constrainedSubsetSum(int[] nums, int k) {

        int n = nums.length;
        int[] num = new int[n + 1];
        int[] f = new int[n + 1];
        for(int i = 1;i <= n;i ++) num[i] = nums[i - 1];

        q.clear();
        for(int i = 1;i <= n;i ++)
        {
            f[i] = num[i];
            while(!q.isEmpty() && i - q.peek().idx > k) q.poll();
            if(!q.isEmpty()) f[i] = Math.max(f[i], q.peek().val + num[i]);
            q.add(new Pair(f[i],i));//把当前点加进优先队列
        }
        //遍历每个位置
        int ans = -0x3f3f3f3f;
        for(int i = 1;i <= n;i ++) ans = Math.max(ans, f[i]);
        return ans;
    }
}
class Pair
{
    int val,idx;
    Pair(int val,int idx)
    {
        this.val = val;
        this.idx = idx;
    }
}