树链剖分

通给给树中所有节点重新编号，使得树中任意一条路径变成 O(logn) 段连续区间。

换句话说，树链剖分的作用 即为：给定 任意一棵树，将树中 所有点 按一定规律 进行编号，使之变成 一条链（一段序列）。转变完成后，树中的任意一条路径 都可以转化成 这个序列中 logn 段连续的区间。

这样一来，对于 树中路径的问题，就可以顺利转化成 区间问题。

例如，我们如果想要求得 树中某个路径中每个节点的权值之和，或者 将某条路径整体加上一个数，等一系列问题，我们就可以将其转化成 区间问题 进行解决，之后我们一般可以用 线段树 进行 区间 问题的维护，当然还可以用 树状数组 等一系列可用于 维护区间的数据结构（核心思想）

接下来咱们看看它是如何 具体操作 的：（如何 将一棵树转化成一个序列，以及 如何将树中每条路径转化成不超过 logn 段连续区间）

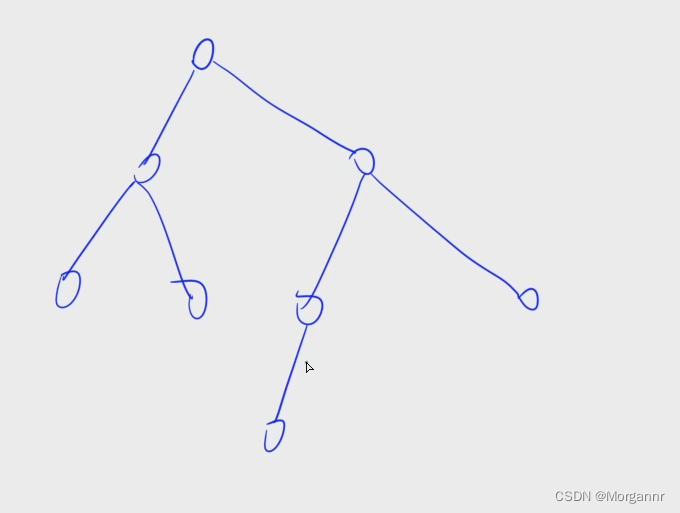
首先我们来 构建一棵树：

STEP I 概念介绍

先来定义 几个概念：
* （1）“重儿子” 和 “轻儿子”

我们先将所有儿子分为 两种：“重儿子” 和 “轻儿子”，注意，对于 叶子结点 没有 “儿子” 这个概念。对于树中的 任意一个节点，这里我们就以 根节点 为例，可以将它所有的儿子 分为两类，首先求一下 其每棵子树 的 节点总数。

就上图而言，根节点 左侧第一棵子树共有 3 个节点，右侧第一棵子树共有 4 个节点，显然 节点个数最多 的是 右侧 这棵子树，那么 右侧子树的根 即为 其父节点的“重儿子”，对应下图即为 红色节点。

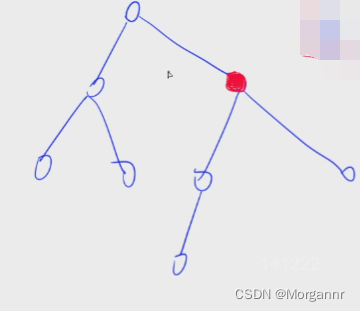
注意，如果 有多棵子树的节点数达到最大值，那么 任选一棵子树的根节点 作为 “重儿子” 即可。

除了重儿子外的儿子就被称为 “轻儿子”。

以此类推，下图中 4 个 “红色节点” 都是其父节点的 “重儿子”。 其余的即为 “轻儿子”。

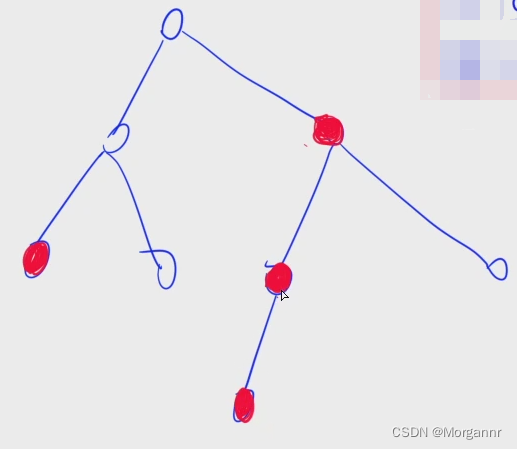
• （2）“重边” 和 “轻边”

“重儿子” 对应 “重边”，“轻儿子” 对应 “轻边”。

即，“重儿子” 和 其父节点 连上的边即为 “重边”，“轻儿子” 和 其父节点 连上的边即为 “轻边”（除了 “重边” 之外 的所有边都被称为 “轻边”）。

对应下图，所有 红色的边 即为 “重边”

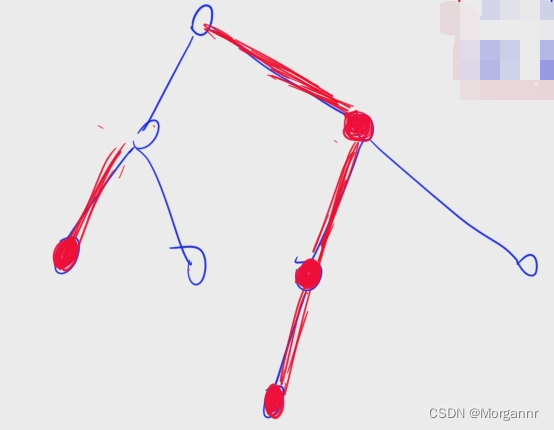
* （3）“重链”

这个概念只针对于 “重边”。

“重链”，即 极大 由重边构成的路径，对应下图 红色框下路径 即为 “重链”。

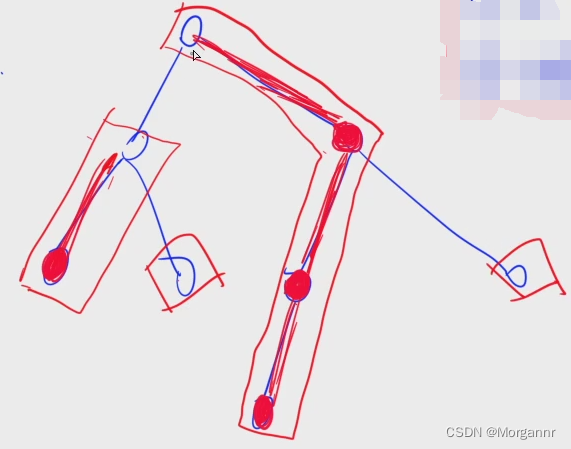
在上图中，我们发现有两个 “重链” 都是 单独的节点，这是因为：我们 要将每个节点都放到一条 “重链” 中。

在这里我们还可以发现，重链的开头一定是轻儿子。

STEP II 两遍dfs预处理（核心）

介绍完概念后，我们提一个很重要的结论，这也是 树链剖分 的 核心点：

• 将树中 所有点和边 分类完成以后，树中任意一条路径均可拆分成 O(logn) 个连续区间 。

那么，如何将当前树变成一段序列呢？我们直接用 这棵树的 dfs序，所谓 dfs 序，之前也有所接触过，即 在 dfs 的过程中，按顺序遍历每个点 的次序。

以根节点作为第 1 个点 开始遍历，遍历过程中，我们 优先遍历当前点的 “重儿子”。

如图，节点上方标明的数字即为 dfs遍历 时的顺序。

这样遍历的 好处：保证 “重链” 上所有点的编号都是连续的。

这样一来，我们就将一棵树按照其 dfs序 转变成一条 链。

小结一下：（通过下面两步就可以将整棵树变成一段 dfs 序，同时也可以标记处每条 重链）
* 第一步，先通过 dfs 标记树中 每个点的重儿子，即在 dfs 过程中记录每一棵子树的大小，递归完所有儿子后，判断哪一棵子树节点个数最多，该子树根节点即为重儿子，标记一下。
第一遍 dfs 代码片段：（同时预处理的 depth 数组是方便后续 爬山法 的使用）

void dfs1(int u, int father, int dep)   //节点编号 其父节点编号 当前深度
{
    depth[u] = dep, fa[u] = father, sz[u] = 1;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        dfs1(j, u, dep + 1);
        sz[u] += sz[j]; //当前子树大小加上第 j 棵子树大小 
        if (sz[son[u]] < sz[j]) son[u] = j; //如果当前重儿子节点个数小于第 j 棵子树的节点数，说明当前重儿子应当为 j
    }
}

• 第二步，标记了重儿子之后，再进行一遍 dfs，就可以找出 每一条重链 了。在 第二次 dfs 同时 我们可以得到 dfs 序，同时 将每条重链标记（只需标记 重链上的每个点的顶点 即可，比如在上图中，一条重链上的 2、3、4 号节点的顶点都为 1 号点）
  第二遍 dfs 代码片段：（优先遍历重儿子，其好处前文已经提及）

void dfs2(int u, int t) //当前点 以及当前点所在重链的顶点
{
    id[u] = ++cnt; //dfs序
    nw[cnt] = w[u]; //dfs序中第cnt个点权为w[u]
    top[u] = t; //当前点所在重链的顶点是t
    if (!son[u]) return;    //如果当前点是叶子节点，即没有儿子
    dfs2(son[u], t);    //否则优先搜索其重儿子
    //之后dfs所有轻儿子
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        //如果xx或j为其重儿子，由于重儿子已被搜过，那么跳过当前循环
        if (j == fa[u] || j == son[u]) continue;
        dfs2(j, j); //递归轻儿子，轻儿子所在重链顶点就是自己
    }
}

STEP III 爬山法 将任意路径拆分成区间（查询 or 修改时）

上面两步完成后，现在我们想 查询某条路径或修改某条路径的值 时，我们就要考虑 如何 将树中 任意一条路径 拆分成 O(logn) 个连续的区间（即 重链）？

这其实是一个 类似于求 LCA 的过程：（爬山法）

• 树中有 两个节点 a、b，之间有一条路径，现在要将该路径拆分为 若干条重链。每次 我们都分别 找到 a、b 两点所在的重链，每次找到 重链顶点深度较大（较 “矮”）的节点，并走到其 父节点，迭代往上走（b 节点所在的另一边 也同理），最终，两点 一定会走到 同一条重链上（即 两点 LCA 所在的重链），两点中间的部分 就是路径的 最后一段。

代码片段：（由于查询路径和修改路径形式一样，我们这里就以修改为例子）

void modify_path(int u, int v, int k)   //爬山法
{
    //如何判断两点是否在同一条重链中？
    //类似于并查集 存了每个点所在重链的顶点编号
    //判断两点所在重链顶点是否一样即可
    while (top[u] != top[v])    //当两点不在同一条重链中时
    {
        if (depth[top[u]] < depth[top[v]]) swap(u, v);
        //优先走u所在重链
        modify(1, id[top[u]], id[u], k);    //修改这段连续区间 即子树
        u = fa[top[u]]; //跳到重链上方
    }
    if (depth[u] < depth[v]) swap(u, v);
    modify(1, id[v], id[u], k); //修改最后一段
}

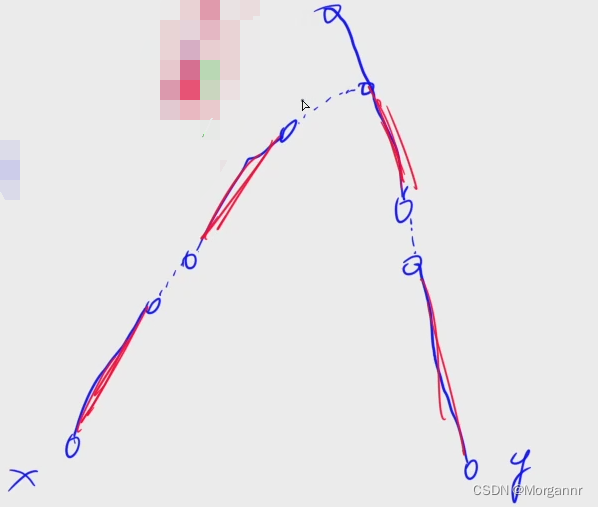
通过上面这样的方式，我们就 将 a、b 两点之间的路径拆分为若干条重链，个数为 O(logn) 级别。现在我们成功将树上问题转化成 logn 个区间问题，之后用 线段树 或者 其它数据结构 求解，时间复杂度 O(n * (logn ^ 2))。如下图所示，红色部分为 重链。

STEP IV 例题

来看一道具体的例题，

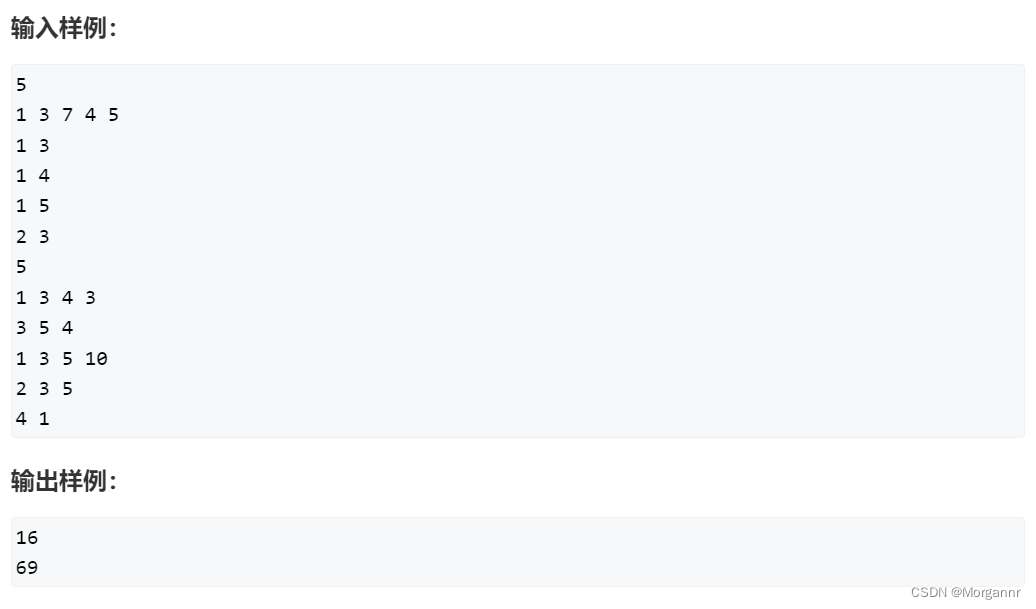
题意：

给定一棵树，要求实现 四种操作：
将两个节点之间路径上所有点的权值加上一个值
将某棵子树中所有点的权值加上一个值
询问两点之间路径上所有点的权值之和
询问某棵子树中所有点的权值之和

思路：

依据 树链剖分 作为解题思想，详见上方的思想讲解。

时间复杂度：

$O(n * (logn) ^ 2)$

代码：

#include <bits/stdc++.h>

using namespace std;
//#define map unordered_map
#define int long long
const int N = 1e5 + 10, M = N << 1;
int n, m;
int h[N], e[M], ne[M], w[N], idx;
int depth[N], fa[N], sz[N], son[N], top[N];
int id[N], nw[N], cnt;

struct node
{
    int l, r;
    int add, sum;
} t[N << 2];

inline void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs1(int u, int father, int dep)
{
    depth[u] = dep, fa[u] = father, sz[u] = 1;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        dfs1(j, u, dep + 1);
        sz[u] += sz[j];
        if (sz[son[u]] < sz[j]) son[u] = j;
    }
}

void dfs2(int u, int t)
{
    id[u] = ++cnt, nw[cnt] = w[u], top[u] = t;
    if (!son[u]) return;
    dfs2(son[u], t);
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == fa[u] || j == son[u]) continue;
        dfs2(j, j);
    }
}

void pushup(int u) {
    t[u].sum = t[u << 1].sum + t[u << 1 | 1].sum;
}

void pushdown(int u) {
    auto& rt = t[u], & le = t[u << 1], & ri = t[u << 1 | 1];
    if (rt.add)
    {
        le.add += rt.add, le.sum += rt.add * (le.r - le.l + 1);
        ri.add += rt.add, ri.sum += rt.add * (ri.r - ri.l + 1);
        rt.add = 0;
    }
}

void build(int u, int l, int r)
{
    t[u] = { l, r };
    if (l == r) {
        t[u].sum = nw[r];//////////
        return;
    }
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

void modify(int u, int l, int r, int v)
{
    if (l <= t[u].l && r >= t[u].r)
    {
        t[u].add += v, t[u].sum += v * (t[u].r - t[u].l + 1);
        return;
    }
    pushdown(u);
    int mid = t[u].l + t[u].r >> 1;
    if (l <= mid) modify(u << 1, l, r, v);
    if (r > mid) modify(u << 1 | 1, l, r, v);
    pushup(u);
}

int ask(int u, int l, int r)
{
    if (l <= t[u].l && r >= t[u].r)
    {
        return t[u].sum;
    }
    pushdown(u);
    int mid = t[u].l + t[u].r >> 1;
    int res = 0;
    if (l <= mid) res += ask(u << 1, l, r);
    if (r > mid) res += ask(u << 1 | 1, l, r);
    return res;
}

void modify_path(int u, int v, int k)
{
    while (top[u] != top[v])
    {
        if (depth[top[u]] < depth[top[v]]) swap(u, v);
        modify(1, id[top[u]], id[u], k);
        u = fa[top[u]];
    }
    if (depth[u] < depth[v]) swap(u, v);
    modify(1, id[v], id[u], k);
}

int ask_path(int u, int v)
{
    int res = 0;
    while (top[u] != top[v])
    {
        if (depth[top[u]] < depth[top[v]]) swap(u, v);
        res += ask(1, id[top[u]], id[u]);
        u = fa[top[u]];
    }
    if (depth[u] < depth[v]) swap(u, v);
    res += ask(1, id[v], id[u]);
    return res;
}

void modify_tree(int u, int v)
{
    modify(1, id[u], id[u] + sz[u] - 1, v);
}

int ask_tree(int u)
{
    return ask(1, id[u], id[u] + sz[u] - 1);
}

signed main()
{
    cin >> n;
    for (int i = 1; i <= n; ++i) scanf("%lld", &w[i]);
    memset(h, -1, sizeof h);
    int t = n - 1;
    while (t--)
    {
        int x, y; scanf("%lld%lld", &x, &y);
        add(x, y), add(y, x);
    }
    dfs1(1, -1, 1);
    dfs2(1, -1);
    build(1, 1, n);
    cin >> m;
    while (m--)
    {
        int op, u;
        scanf("%lld%lld", &op, &u);
        if (op == 1)
        {
            int v, k; scanf("%lld%lld", &v, &k);
            modify_path(u, v, k);
        }
        else if (op == 2)
        {
            int k; scanf("%lld", &k);
            modify_tree(u, k);
        }
        else if (op == 3)
        {
            int v; scanf("%lld", &v);
            printf("%lld\n", ask_path(u, v));
        }
        else
        {
            printf("%lld\n", ask_tree(u));
        }
    }
    return 0;
}

（代码 + 注释）

#include <bits/stdc++.h>

using namespace std;
//#define map unordered_map
//#define int long long
const int N = 1e5 + 10, M = N << 1;
typedef long long ll;
int n, m;
int h[N], e[M], ne[M], w[N], idx;
int id[N];  //原来树中每个点在dfs序中的编号
int nw[N];  //每个编号点的权值，即新编号的点的权值 dfs序中第i个点编号
int cnt;
int depth[N];   //每个点所在深度
int sz[N];  //以每个点为根节点的子树大小
int top[N]; //每个点所在重链的顶点
int fa[N];  //每个点父节点
int son[N]; //每个点的重儿子

struct node
{
    int l, r;
    ll add, sum;    //线段树中维护两个值 
} t[N << 2];

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs1(int u, int father, int dep)   //节点编号 其父节点编号 当前深度
{
    depth[u] = dep, fa[u] = father, sz[u] = 1;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        dfs1(j, u, dep + 1);
        sz[u] += sz[j]; //当前子树大小加上第 j 棵子树大小 
        if (sz[son[u]] < sz[j]) son[u] = j; //如果当前重儿子节点个数小于第 j 棵子树的节点数，说明当前重儿子应当为 j
    }
}

void dfs2(int u, int t) //当前点 以及当前点所在重链的顶点
{
    id[u] = ++cnt; //dfs序
    nw[cnt] = w[u]; //dfs序中第cnt个点权为w[u]
    top[u] = t; //当前点所在重链的顶点是t
    if (!son[u]) return;    //如果当前点是叶子节点，即没有儿子
    dfs2(son[u], t);    //否则优先搜索其重儿子
    //之后dfs所有轻儿子
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        //如果xx或j为其重儿子，由于重儿子已被搜过，那么跳过当前循环
        if (j == fa[u] || j == son[u]) continue;
        dfs2(j, j); //递归轻儿子，轻儿子所在重链顶点就是自己
    }
}

void pushup(int u)
{
    t[u].sum = t[u << 1].sum + t[u << 1 | 1].sum;
}

void pushdown(int u)    //下传懒标记
{
    auto &rt = t[u], &le = t[u << 1], &ri = t[u << 1 | 1];
    if (rt.add)
    {
        le.add += rt.add, le.sum += rt.add * (le.r - le.l + 1);
        ri.add += rt.add, ri.sum += rt.add * (ri.r - ri.l + 1);
        rt.add = 0;
    }
}

void build(int u, int l, int r)
{
    t[u] = { l, r };
    if (l == r) {
        t[u].sum = nw[l];
        return;
    }
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

void modify(int u, int l, int r, int v)
{
    if (l <= t[u].l && r >= t[u].r)
    {
        t[u].add += v, t[u].sum += v * (t[u].r - t[u].l + 1);
        return;
    }
    pushdown(u);
    int mid = t[u].l + t[u].r >> 1;
    if (l <= mid) modify(u << 1, l, r, v);
    if (r > mid) modify(u << 1 | 1, l, r, v);
    pushup(u);
}

ll ask(int u, int l, int r)
{
    if (l <= t[u].l && r >= t[u].r)
    {
        return t[u].sum;
    }
    pushdown(u);
    int mid = t[u].l + t[u].r >> 1;
    ll res = 0;
    if (l <= mid) res += ask(u << 1, l, r);
    if (r > mid) res += ask(u << 1 | 1, l, r);
    return res;
}

void modify_path(int u, int v, int k)   //之前说的爬山法
{
    //如何判断两点是否在同一条重链中？
    //类似于并查集 我存了每个点所在重链的顶点编号
    //判断两点所在重链顶点是否一样即可
    while (top[u] != top[v])    //当两点不在同一条重链中时
    {
        if (depth[top[u]] < depth[top[v]]) swap(u, v);
        //优先走u所在重链
        modify(1, id[top[u]], id[u], k);    //修改这段连续区间 即子树
        u = fa[top[u]]; //跳到重链上方
    }
    if (depth[u] < depth[v]) swap(u, v);
    modify(1, id[v], id[u], k); //修改最后一段
}

ll ask_path(int u, int v)   //与修改形式一样
{
    ll res = 0;
    while (top[u] != top[v])
    {
        if (depth[top[u]] < depth[top[v]]) swap(u, v);
        res += ask(1, id[top[u]], id[u]);
        u = fa[top[u]];
    }
    if (depth[u] < depth[v]) swap(u, v);
    res += ask(1, id[v], id[u]);
    return res;
}

void modify_tree(int u, int v)  //以u为子树是一段连续区间，左右端点如下
{
    modify(1, id[u], id[u] + sz[u] - 1, v);
}

ll ask_tree(int u)
{
    return ask(1, id[u], id[u] + sz[u] - 1);
}

signed main()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
    {
        scanf("%d", &w[i]);
    }
    memset(h, -1, sizeof h);
    int t = n - 1;
    while (t--)
    {
        int u, v; scanf("%d%d", &u, &v);
        add(u, v), add(v, u);
    }

    dfs1(1, -1, 1); //先求每个点的重儿子
    dfs2(1, -1);    //求一下 dfs 序
    build(1, 1, n); //建线段树

    //树链剖分
    cin >> m;
    while (m--)
    {
        int t, u, v, k; scanf("%d%d", &t, &u);
        if (t == 1)
        {
            scanf("%d%d", &v, &k);
            modify_path(u, v, k);
        }
        else if (t == 2)
        {
            scanf("%d", &k);
            modify_tree(u, k);
        }
        else if (t == 3)
        {
            scanf("%d", &v);
            printf("%lld\n", ask_path(u, v));
        }
        else
        {
            printf("%lld\n", ask_tree(u));
        }
    }

    return 0;
}