<---大佬们点个赞吧qwq

$$\huge\color{orange}{→→→暑假每日一题2022题解合集←←←}$$
$\ $
$\ $

题目描述

笛卡尔树 是由一系列不同数字构成的二叉树。

树是堆排序的，中序遍历返回原始序列。

例如，给定序列 $\{ 8, 15, 3, 4, 1, 5, 12, 10, 18, 6 \}$，则生成的最小堆笛卡尔树如图所示。

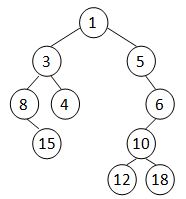
现在，给定一个长度为 $N$ 的原始序列，请你生成最小堆笛卡尔树，并输出其层序遍历序列。

输入格式

第一行包含整数 $N$。

第二行包含 $N$ 个两两不同的整数，表示原始序列。

输出格式

共一行，输出最小堆笛卡尔树的层序遍历序列。

数据范围

$1 \\le N \\le 30$,
原始序列中元素的取值范围 $\[-2147483648,2147483647\]$。

输入样例：

10
8 15 3 4 1 5 12 10 18 6

输出样例：

1 3 5 8 4 6 15 10 12 18

算法

(dfs, bfs) $O(n)$

先用 dfs 建树，然后用 bfs 输出答案

时间复杂度

无论 dfs 还是 bfs 每个点都只遍历一次，所以时间复杂度 $O(n)$。

空间复杂度

dfs 的空间复杂度是树的深度，最多为 $O(n)$，bfs 的空间复杂度最多是节点数也就是 $O(n)$，总的空间复杂度就是 $O(n)$。

C++ 代码

#include <iostream>
#include <queue> // bfs要用

using namespace std;

const int N = 35;

int n;
int s[N]; // 原始序列

struct Node
{
    int l, r, dat;
}tree[N]; // 笛卡尔树
int cnt; // 树的长度，便于加入元素

int dfs(int l, int r) // 建s[l] ~ s[r]的笛卡尔树，返回根节点
{
    if (l >= r) return -1; // 如果区间不合法返回-1

    int minv = 2147483647, idx; // minv: s[l] ~ s[r]中最小的数，idx: 它的编号
    for (int i = l; i < r; i ++ ) // 遍历s[l] ~ s[r]
        if (minv >= s[i]) // 如果能更新
            minv = s[i], idx = i; // 更新

    int tmp = cnt; // 根节点编号需要保存一下，因为往深层递归的时候可能会改动cnt

    tree[cnt ++ ] = {dfs(l, idx), dfs(idx + 1, r), minv}; // 往深层递归

    return tmp; // 返回根节点编号
}

void bfs() // 输出最小堆笛卡尔树的层序遍历序列
{
    queue<int> q; // bfs要用的队列
    q.push(0); // 把根节点加入队列（因为根节点是最先遍历的，所以它的编号总是0

    while (!q.empty()) // 还能扩展
    {
        int t = q.front(); // 要扩展的点
        cout << tree[t].dat << ' '; // 输出
        q.pop(); // 出队

        if (~tree[t].l) q.push(tree[t].l); // 如果左儿子非空则加入队列
        if (~tree[t].r) q.push(tree[t].r); // 同理
    }
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> s[i]; // 输入原始序列

    dfs(0, n); // dfs
    bfs(); // bfs

    return 0;
}