<—点个赞吧QwQ

宣传一下算法提高课整理{:target=”_blank”}

Alice和Bob玩了一个古老的游戏：首先画一个 $n \\times n$ 的点阵（下图 $n = 3$ ）。

接着，他们两个轮流在相邻的点之间画上红边和蓝边：

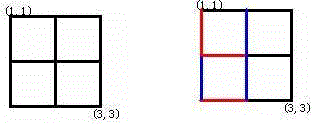
直到围成一个封闭的圈（面积不必为 $1$）为止，“封圈”的那个人就是赢家。因为棋盘实在是太大了，他们的游戏实在是太长了！

他们甚至在游戏中都不知道谁赢得了游戏。

于是请你写一个程序，帮助他们计算他们是否结束了游戏？

输入格式

输入数据第一行为两个整数 $n$ 和 $m$。$n$表示点阵的大小，$m$ 表示一共画了 $m$ 条线。

以后 $m$ 行，每行首先有两个数字 $(x, y)$，代表了画线的起点坐标，接着用空格隔开一个字符，假如字符是 $D$，则是向下连一条边，如果是 $R$ 就是向右连一条边。

输入数据不会有重复的边且保证正确。

输出格式

输出一行：在第几步的时候结束。

假如 $m$ 步之后也没有结束，则输出一行“draw”。

数据范围

$1 \\le n \\le 200$，
$1 \\le m \\le 24000$

输入样例：

3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D

输出样例：

4

思路

读题目可知谁先画成一个环，谁就赢。

如何判断是否形成一个环？假设当前添加的边是 $(a,b)$（$a,b$ 均表示一个点），那么连完后是环的话一定满足 $(a,b)$ 原来就连接，在并查集中，就是满足 $a,b$ 在同一集合。

至此，这题就做完了，注意一下并查集的下标用一位数方便，于是我们可以把坐标为 $(i,j)$ 的点换成编号为 $i*n+j$ 的点方便实现。（不知道原理的自己百度）

代码

#include <iostream>
using namespace std;
const int N = 40010;
int n,m;
int p[N];
int get (int x,int y) {
    return x*n+y;
}
int find (int x) {
    if (p[x] != x) p[x] = find (p[x]);
    return p[x];
}
int main () {
    cin >> n >> m;
    for (int i = 0;i < n*n;i++) p[i] = i;
    int ans = 0;
    for (int i = 1;i <= m;i++) {
        int x,y;
        char ch;
        cin >> x >> y >> ch;
        x--,y--;
        int a = get (x,y),b;
        if (ch == 'R') b = get (x,y+1);
        else b = get (x+1,y);
        int pa = find (a),pb = find (b);
        if (pa == pb) {
            cout << i << endl;
            return 0;
        }
        p[pa] = pb;
    }
    cout << "draw" << endl;
    return 0;
}