类似题：
乘积小于k的子数组

算法1

(前缀和) $O(n)$

这道题s是循环数组，如果在s上循环对于结束条件就很难把握

那么我们来看p有什么性质

借用负雪明烛大佬的图

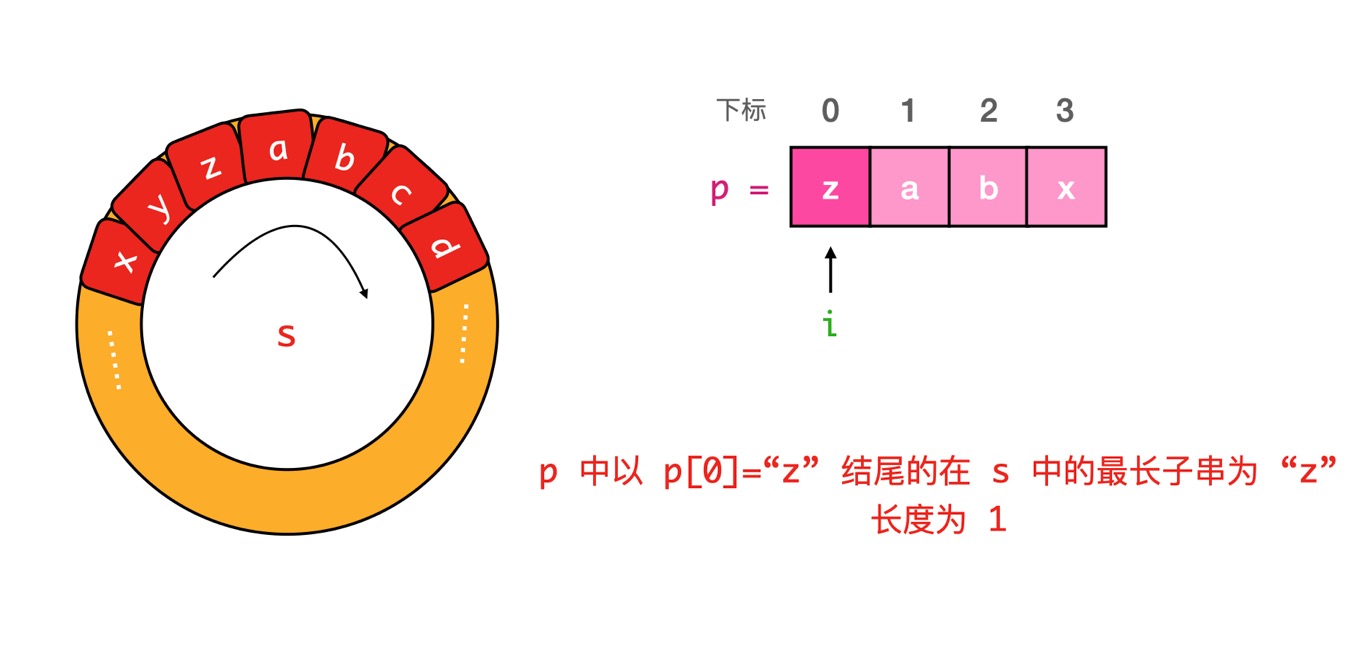
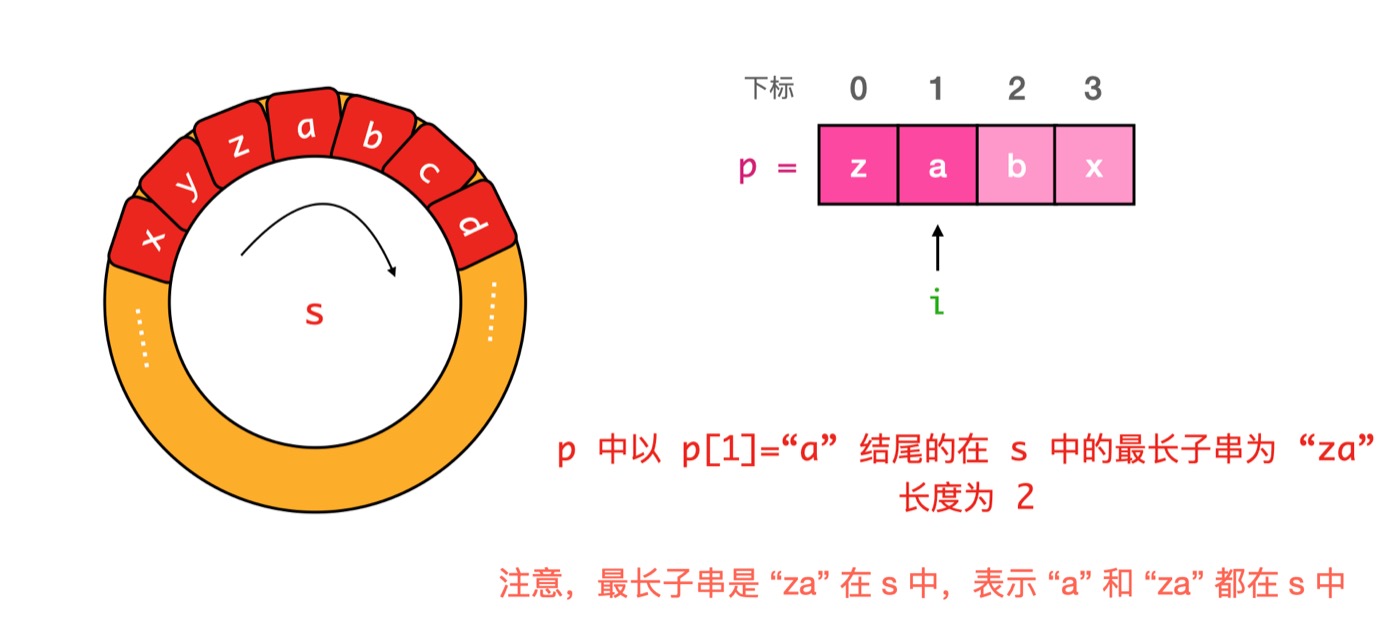
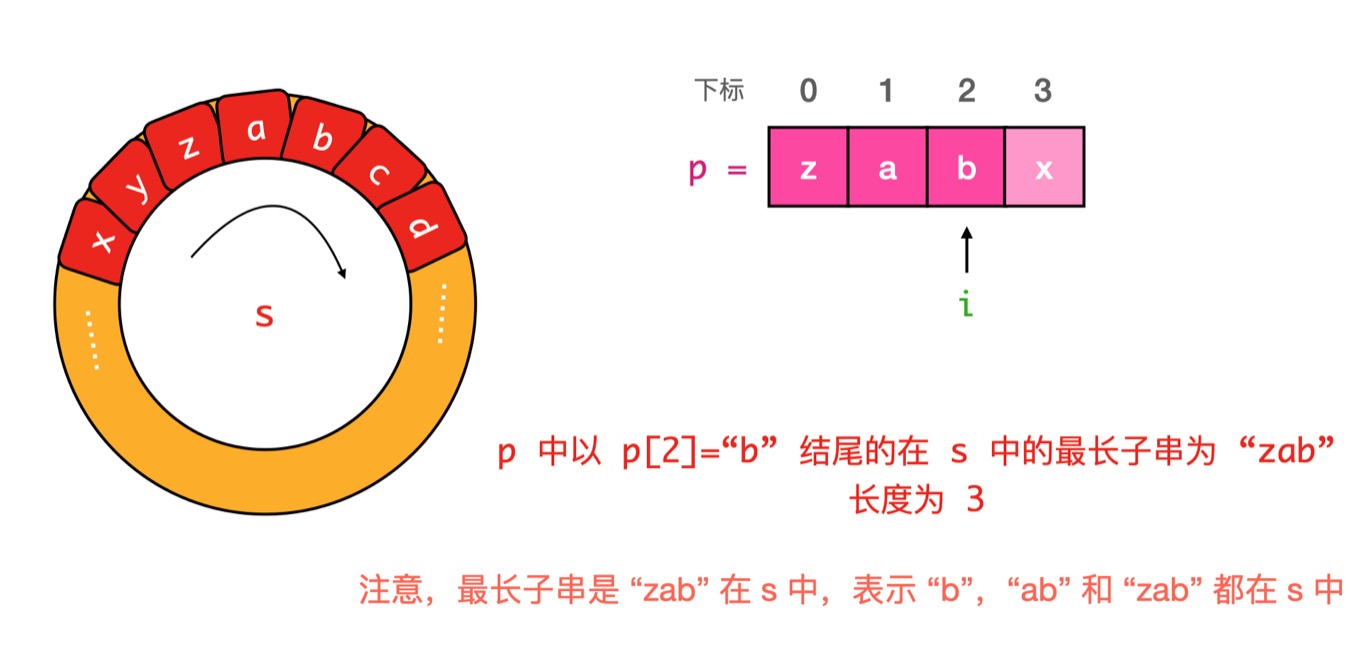
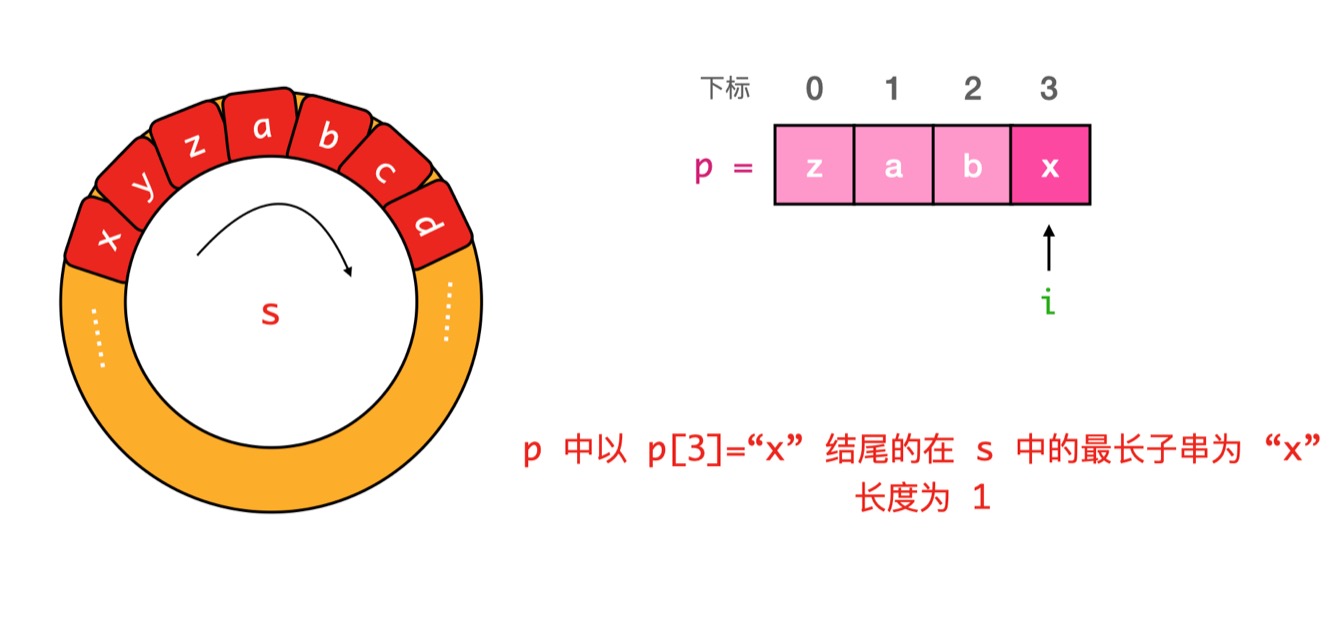
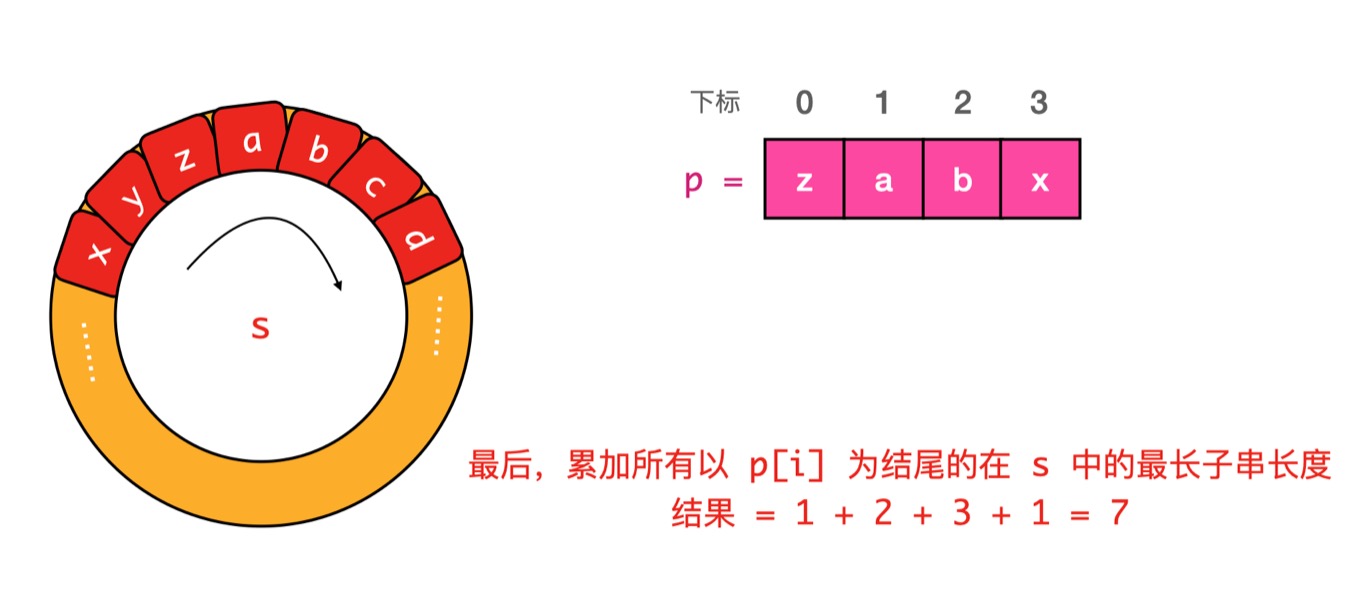
我们可以注意到 对于连续的字符串 abc有以下性质

以a结尾的子串为1

以b结尾的子串为2

以c结尾的子串为3

但是本题是要满足在字母序循环数组中的字符串子串

那么我们就从p的第二个字母开始计算

有两种情况

• 这个字母与前一个字母相邻
  *如果相邻那么就按照上面的通用情况来计算子串数量
• 这个字母与前一个字母不相邻
  *如果不相邻，那么就在这个字母开始重新计算相邻子串数量

要注意到 在遍历过程中 以某个字母结尾的子串可能会出现重复的情况

如 p = cabc
cnt[c] = 1
cnt[a] = 1
cnt[b] = 2
cnt[c] = 3

此时我们只需要取最大值即可 即cnt[c] = 3 ,总数量为 1 + 2 + 3 = 6

C++ 代码

class Solution {
public:
    int findSubstringInWraproundString(string p) {
        int n = p.size();
        int cnt[26]{0}; //记录以每个字母结尾的子串数量

        int tmp = 1;//记录连续的子串
        cnt[p[0] - 'a'] = 1;//将p中首字母子串数放入cnt
        for(int i = 1; i < n; i++)
        {
            if((p[i] - p[i - 1] + 26) % 26 == 1)
            {
                tmp++;
                cnt[p[i] - 'a'] = max(cnt[p[i] - 'a'],tmp);
            }
            //如果前后字母不相邻，tmp重新计算
            else
            {
                tmp = 1;
                cnt[p[i] - 'a'] = max(cnt[p[i] - 'a'],1);
            }
        }

        int res = 0;
        for(int i = 0; i < 26; i++)
            res += cnt[i];

        return res;
    }
};