题目背景

给定一个长度为 m 的模式串 S，以及一个长度为 n 的模板串 P，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模板串 P 在模式串 S 中多次作为子串出现。

求出模板串 P 在模式串 S 中所有出现的位置的起始下标。

Solution 1 :KMP $O(n + m)$

对于 S 中的每一个位置 i ，我们都要找到一个最大的 j 使得 P 的长度为j的前缀(P[1] -> P[j])和 包含 S[i] 的 i 位置的长度为 j 的前缀(S[i - j + 1] -> S[i])相同。

假设我们匹配到了当前位置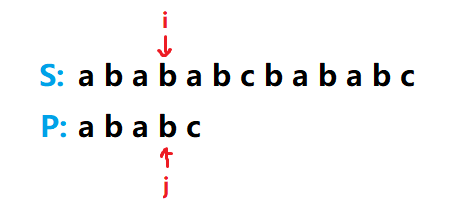

此时我们需要分情况讨论：

1.如果 S[i + 1] = P[j + 1] 我们就可以继续向下匹配

2.如果 S[i + 1] != P[j + 1], 我们无法继续向下匹配了

那我们需要从头开始匹配吗？ 不需要

我们需要找到一个最大的的位置 k 使得 P 的长度为k的前缀(P[1] -> P[k])和包含 S[i] 的 i 位置的长度为 k 的前缀(S[i - k + 1] -> S[i])相同。

由于i ,j 之前的位置都是匹配好的，因此(S[i - k + 1] -> S[i]) 和(P[j - k + 1] -> P[j])是完全相同的

因此我们可以将问题转化成：
我们需要找到一个最大的的位置 k 使得 P 的长度为k的前缀(P[1] -> P[k])和包含 P[j] 的 j 位置的长度为 k 的前缀(P[j - k + 1] -> P[j])相同。

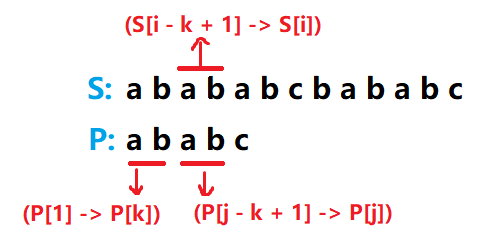
问题从两个串的问题变成了 P 串中的问题

对于 P 中的每一个位置 j 我们都可以找到一个对应的位置 k ,将所有 k 的位置存在一个next数组里， 用于匹配失败之后的状态转移。

整理一下KMP的思路：

1.两串匹配，i 指针遍历 S ，j 指针遍历 P
2.如果s[i + 1] = p[j + 1]，就让 j ++ 然后继续匹配
3.如果s[i + 1] != p[j + 1], 就令j = next[j]直到二者可以继续匹配
4.如果 j 匹配到下标为 n 的字符并成功，那么这一轮匹配成功，j = next[j] 再重新进行下一轮匹配直到 i 移动到下标为 m 的字符，整个匹配结束。

如何求next数组呢？

其实求next数组的过程就是 P 串和自己匹配的过程，对于 P 的每一个字符 P[i], 我们都要找到使得 P[j] 的后缀和 P[1]的前缀相同的最大位置next[j]。

C++ Code

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5+10, M = 1e6+10;

char s[M], p[N];
int n,m, ne[N];

int main()
{
    cin >> n >> p + 1 >> m >> s + 1;

    // 求next数组
    ne[1] = 0;
    for(int i = 2, j = 0; i <= n ; ++i){//这里i 和 j 遍历的都是 P 串
        while(j && p[i] != p[j + 1])j = ne[j];
        // 所有需要用到的next值都会在之前的迭代中计算出来, 
        //  字符串下标是从1开始的，因此 j 至少为1时才可以回退
        if(p[i] == p[j + 1])j++; // 如果下一个字符对应相同就继续向下匹配
        ne[i] = j;// 记录每一个i值匹配到的最大前缀
    }

    // KMP 每一步的思路都与上面类似
    for(int i = 1, j = 0; i <= m ; ++i){
        while(j && s[i] != p[j + 1])j = ne[j];
        if(s[i] == p[j + 1])j++;
        if(j == n){ // 匹配成功
            printf("%d ",i - n);
            j = ne[j]; // 再开启下一轮匹配
        }
    }
    return 0;
}

Solution 2:字符串哈希 $O(n + m)$

字符串哈希的具体实现方式可以参考这篇题解

字符串哈希的思路就比较简单了，我们需要算出模板串 P 的哈希值，再与 S 的每一个长度为 n 的字串的哈希值进行比较，这里代码就不再给出详细注释。

C++ Code

#include <bits/stdc++.h>

using namespace std;

typedef unsigned long long ULL;

const int N = 1e5+10, M = 1e6+10, P = 131;
int n,m;
char a[M], b[N];
ULL s[M],p[M];

ULL get(int l, int r){
    return s[r] - s[l - 1]*p[r - l + 1];
}


int main()
{
    cin >> n >> b + 1 >> m >> a + 1;
    p[0] = 1;
    for(int i = 1; a[i] ; ++i){
      p[i] = p[i - 1] * P;
      s[i] = s[i - 1] * P + a[i];
    }

    ULL q[N];
    for(int i = 1; b[i] ; ++i)q[i] = q[i - 1]*P + b[i]; 

    for(int i = 1;  i + n - 1 <= m; ++i){
        if(q[n] == get(i,i + n - 1))cout << i - 1 << " ";
    }
    return 0;
}