算法分析

二次筛法
这里的区间范围给定的最大值是2^31 - 1,而用线性筛法求的是[1,n]中的所有质数，因此直接用线性筛法求肯定会直接gg，因此需要通过挖掘某些性质，才能有技巧性的完成，y总的视频讲得实在太好了，不得不为他点赞

性质

• 性质1：若一个数n是一个合数，必然存在2个因子$d$,$\frac{n}{d}$，假设$d$ <= $\frac{n}{d}$，则$d$ <= $\sqrt n$，因此必然存在一个小于等于 $\sqrt n$的因子

• 性质2：若x$\in$[L,R],且x是合数，则一定存在P <= $\sqrt{2^{31}-1}$ (< 50000)，使得P能整除x，其中P < x.

步骤

• 1、找出1 ~ $\sqrt{2^{31}-1}$ (< 50000)中的所有质因子
• 2、对于1 ~ 50000 中每个质数P，将[L,R]中所有P的倍数筛掉(至少2倍)
  • 找到大于等于L的最小的P的倍数$P_{0}$，找下一个倍数时只需要+= P即可

引理(分数的上取整转换下取整)

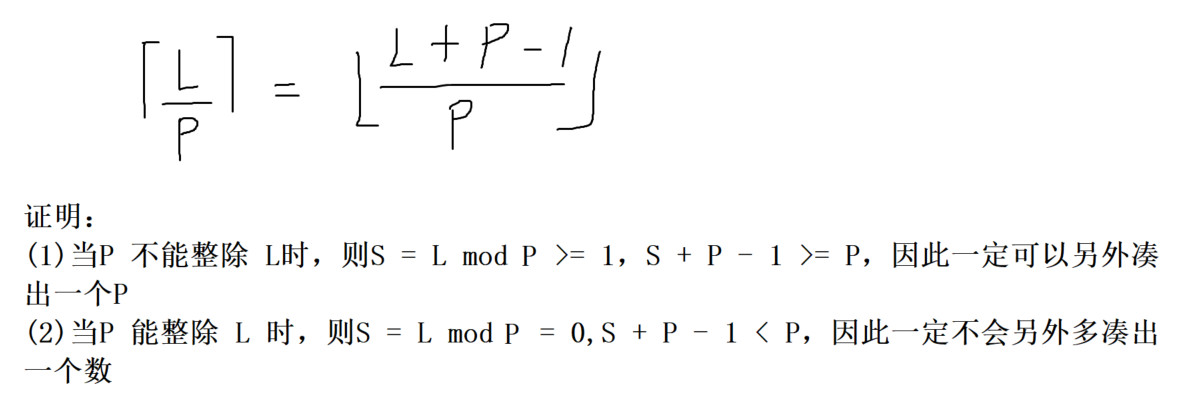
细节

ly20 同学在y总的代码 问的3个很高质量的问题，也是很细节的地方，感谢ly20 同学

• （1）每个质数是2~50000中的数，为啥 LL p = primes[i]; 这里的p的LL啊， int 不就够了吗？
• （2）for (LL j = max(p * 2, (l + p - 1) / p * p); j <= r; j += p) 这里的 j 是小于等于 r 的，而 r 的取值范围是小于2 ^ 31，也是在int 范围内啊， 这里为啥用LL啊？
• （3） 我知道这里是复用st数组，但是在用之前都初始化为0了啊，为什么init(50000); 放在while (cin >> l >> r) 的外面（也就是最前面）代码不行啊？

回答：

• (1)LL p = primes[i]，这里p用LL是因为如果p也是用int类型，本身l也是用int类型，如果l取得足够大，下面的l + p - 1会有可能直接爆int变成负数
• (2)这里的 j 是小于等于 r 的，而 r 的取值范围是小于2 ^ 31,这里确实是这样，可是这个循环跳出的条件是j <= r，也就是说如果r是最大的int，那么当j += p，要超过最大的int的时候需要比它还大才能跳出循环，因此直接爆int变成负数，然后j <= r依然成立，会一直死循环下去
• (3)放在最前面也是可以的，y总的代码中判断从[1,50000]中谁是质数和在区间[L,R]中谁是质数直接复用st[]数组，就不用再开一个数组去存了，也可以把init()放在前面，用一个专门的数组去记录区间[L,R]中谁是质数

时间复杂度 $O(n)$

参考文献

算法提高课

Java 代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N = 50010;
    static int M = 1000010;
    static int[] primes = new int[N];
    static int cnt = 0;
    static boolean[] st = new boolean[N];
    static boolean[] bool = new boolean[M];//存[L,R]的元素是否是质数
    static int[] primes2 = new int[M];
    static void init(int n)
    {
        for(int i = 2;i <= n;i ++)
        {
            if(!st[i]) primes[cnt ++] = i;
            for(int j = 0;primes[j] * i <= n;j ++)
            {
                st[primes[j] * i] = true;
                if(i % primes[j] == 0) break;
            }
        }
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        init(50000);
        while(scan.hasNext())
        {
            int l = scan.nextInt();
            int r = scan.nextInt();
            Arrays.fill(bool, false);
            Arrays.fill(primes2, 0);
            for(int i = 0;i < cnt;i ++)
            {
                long p = primes[i];
                for(long j = Math.max(2 * p, (l + p - 1) / p * p);j <= r;j += p)
                    bool[(int)(j - l)] = true;
            }
            int k = 0;
            for(int i = 0;i <= r - l;i ++)
            {
                if(!bool[i] && i + l >= 2)
                    primes2[k ++] = i + l;
            }
            if(k < 2) System.out.println("There are no adjacent primes.");
            else
            {
                int minp = 0,maxp = 0;//最小、大距离的位置
                for(int i = 0;i + 1 < k;i ++)
                {
                    int d = primes2[i + 1] - primes2[i];
                    if(d < primes2[minp + 1] - primes2[minp]) minp = i;
                    if(d > primes2[maxp + 1] - primes2[maxp]) maxp = i;
                }
                System.out.println(primes2[minp] + "," + primes2[minp + 1] + " are closest, "+ primes2[maxp] +"," + primes2[maxp + 1] + " are most distant.");
            }
        }
    }
}