题目描述

给定一个棋盘$(n,m)$。

每个格子$(i,j)$有一些价值$w[i][j]$，要求两次从左上走到右下最多能够获得多少价值。每个格子的物品只能 取一次。

每次只能选择向下走或者向右走。

（与摘花生类似，不过是计算两次获得的最大价值)

题目分析

类比于摘花生

走一次：

$f[i][j]$：表示所有从$(1,1)$走到$(i,j)$的路径的最大值

$f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j]$

走两次：

$f[i_1][j_1][i_2][j_2]$：表示所有从$(1,1)(1,1)$分别走到$(i_1,j_1)(i_2,j_2)$的路径的最大值。

这里需要考虑同一个格子不能重复选择？

答：只有$i_1 + j_1 == i_2 + j_2$的时候，两条路径的格子才可能重合。

于是我们可以使用一个变量k来记录$k = i_1 + j_1 == i_2 + j_2$。k表示的是两条路径当前走到的格子的横纵坐标之和。

接着我们的状态就可以由$f[i_1][j_1][i_2][j_2]$优化为$f[k][i_1][i_2]$三维。这里的k还有着保持两条路线的同步，也就是说两条路线是同步进行的，你走一步，我也跟着走一步。

最终答案就是$f[n + m][n][n]$：两条路线分别走到$(n + m - n, n)，(n + m - n, n)$的方案最大值。

[注]：与方格取数有所不同的是

1. 此题是区域为$(n, m)$
2. 最终答案是$f[n + m][n][n]$

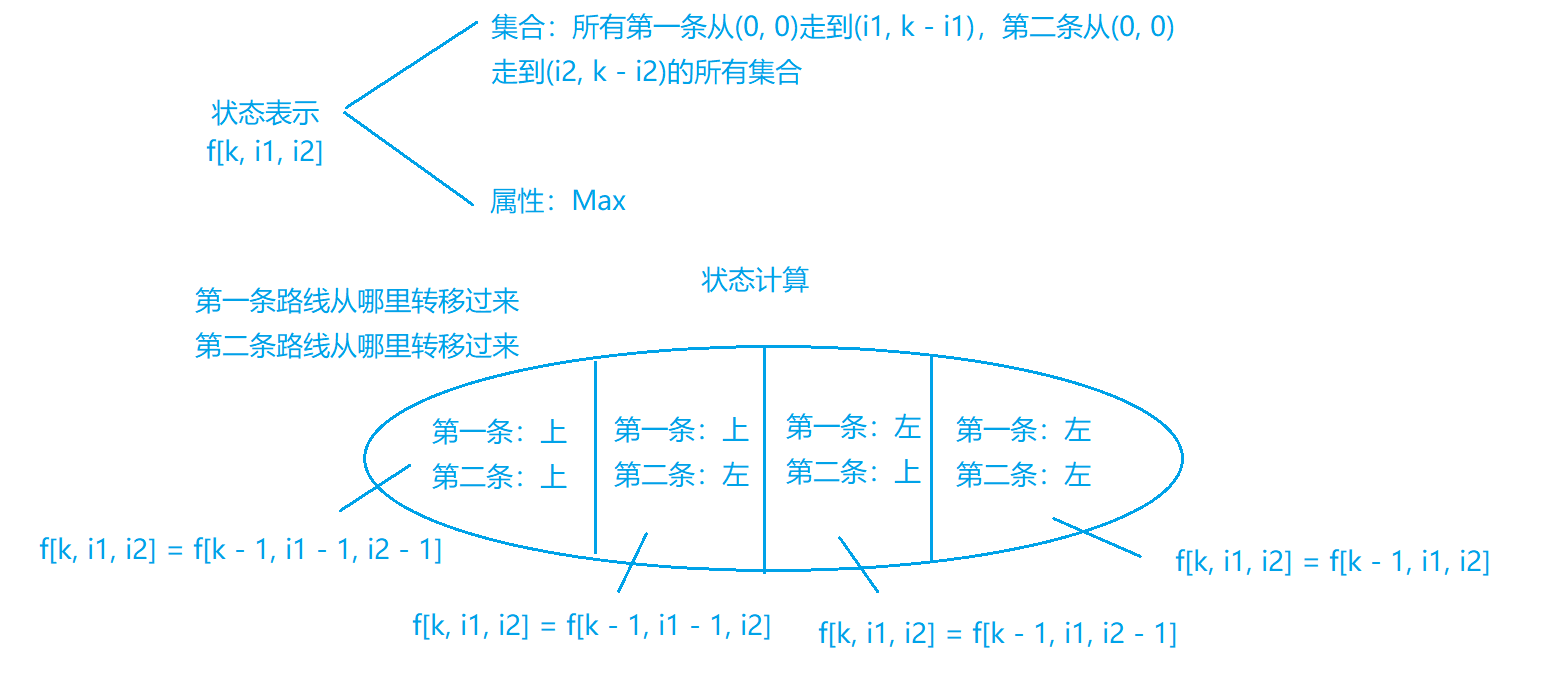
闫式DP分析法

$Code$

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 60;

int n, m;
int w[N][N];
int f[N * 2][N][N];

int main()
{
    cin >> n >> m;

    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
            cin >> w[i][j];

    for(int k = 1; k <= n + m; k ++ )
        for(int i1 = 1; i1 <= n; i1 ++ )
            for(int i2 = 1; i2 <= n; i2 ++ )
            {
                int j1 = k - i1, j2 = k - i2;
                if(j1 < 0 || j2 < 0) continue;
                int v = w[i1][j1];
                if(i1 != i2) v += w[i2][j2];

                int &t = f[k][i1][i2];
                t = max(t, f[k - 1][i1 - 1][i2 - 1]);
                t = max(t, f[k - 1][i1 - 1][i2]);
                t = max(t, f[k - 1][i1][i2 - 1]);
                t = max(t, f[k - 1][i1][i2]);

                t += v;
            }

    cout << f[n + m][n][n] << endl;

    return 0;
}