题目描述

给定一个棋盘$(n,m)$。

每个格子$(i,j)$有一些价值$w[i][j]$，要求从左上走到右下最少能够获得多少价值。

每次只能选择向下走或者向右走。

（与摘花生类似，不过是最少获得的价值）

题目分析

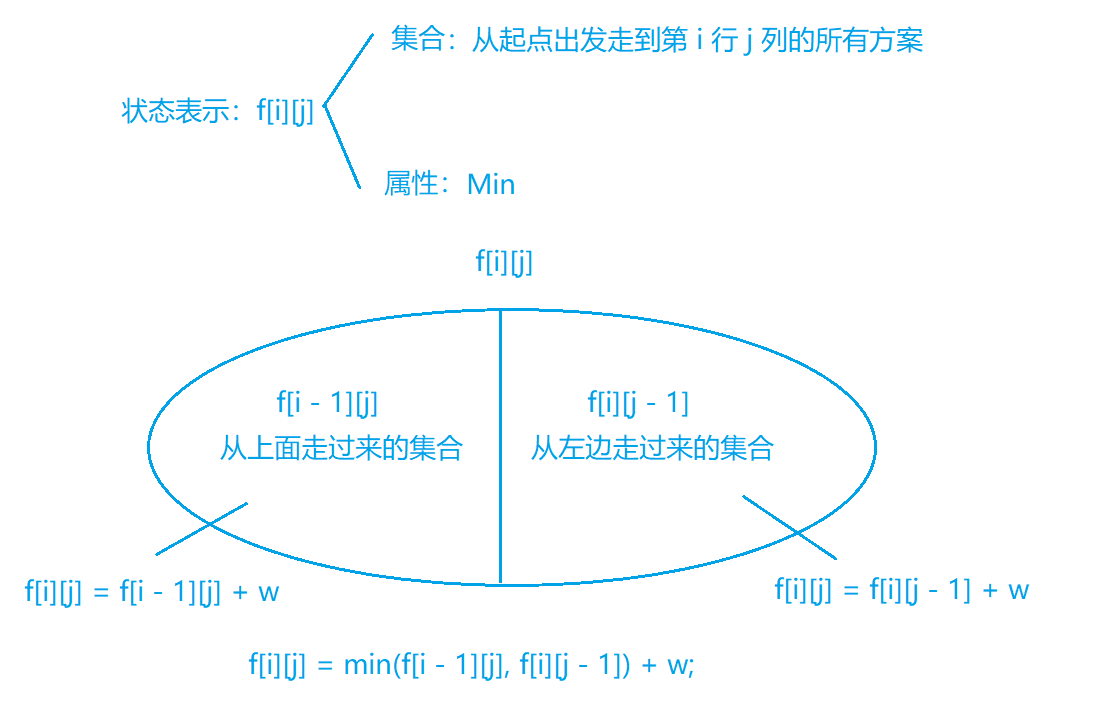
我们可以用$f[i][j]$用来记录走到$(i,j)$这个格子获得的最小价值。

由于每一次的选择只有两种：向下走或者向右走，很容易想到当前格子的最小价值只能由上面两种状态转移过来。

于是计算方式就是f[i][j] = min(f[i - 1][j], f[i][j - 1]) + w[i][j]：要么从$(i,j - 1)$左边走过来，要么从$(i - 1, j)$上面走过来，无论怎么走，都会走到$(i,j)$这个格子，则需要加上$w[i][j]$的价值。

于是最终答案就是$f[n][m]$

注意：此题需要将$f[][]$除了$f[1][0]$和$f[0][1]$之外的点都初始化为正无穷，因为是求最小价值，只有$f[1][1]$有初始值，而$f[i][j] = min(f[i - 1][j], f[i][j - 1]) + w[i][j]$得来的。

$Code$

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 110;

int n;
int w[N][N];
int f[N][N];

int main()
{
    cin >> n;

    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= n; j ++ )
            cin >> w[i][j];

    memset(f, 0x3f, sizeof f);
    f[0][1] = f[1][0] = 0;

    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= n; j ++ )
            f[i][j] = min(f[i - 1][j], f[i][j - 1]) + w[i][j];

    cout << f[n][n] << endl;        

    return 0;
}