题目描述

Given a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle.

Example 1:

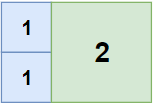
Input: n = 2, m = 3
Output: 3
Explanation: 3 squares are necessary to cover the rectangle.
2 (squares of 1x1)
1 (square of 2x2)

Example 2:

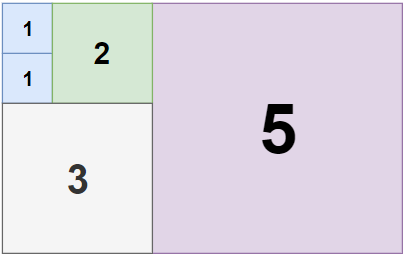
Input: n = 5, m = 8
Output: 5

Example 3:

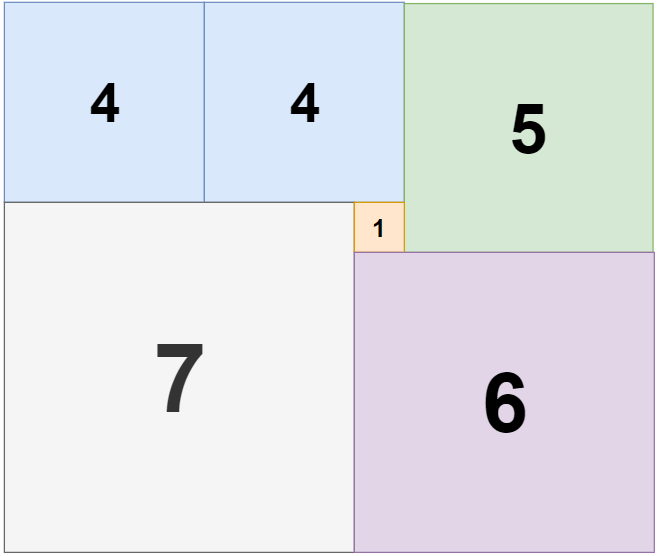
Input: n = 11, m = 13
Output: 6

Constraints:

• 1 <= n, m <= 13

算法1

(暴力枚举)

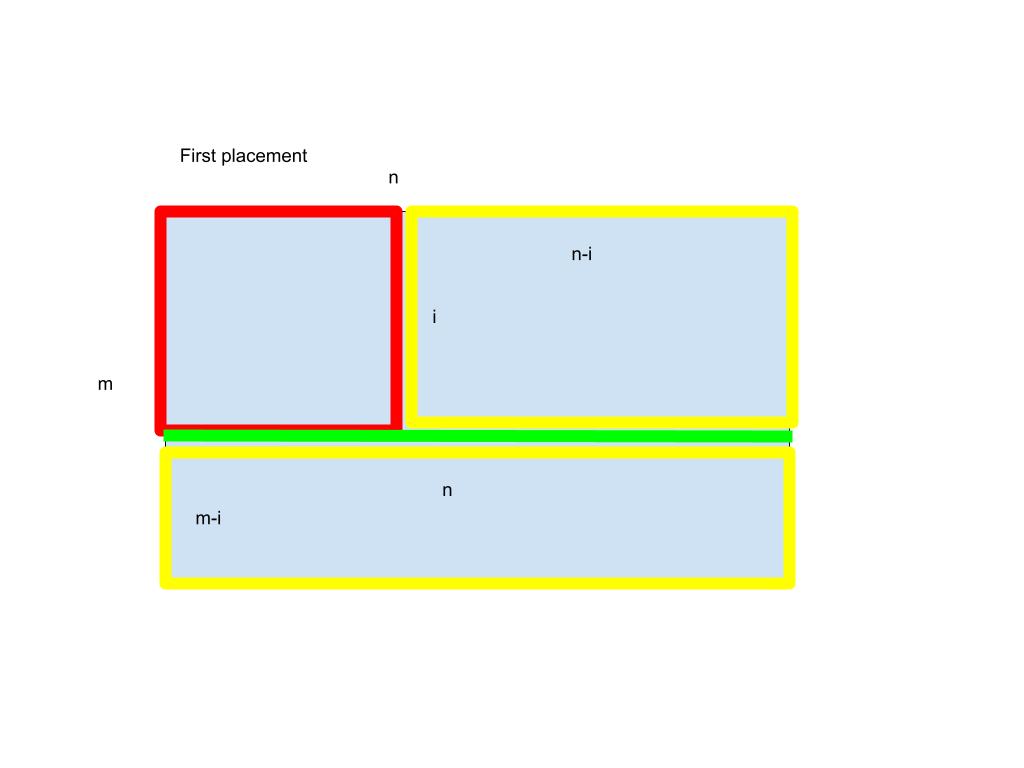
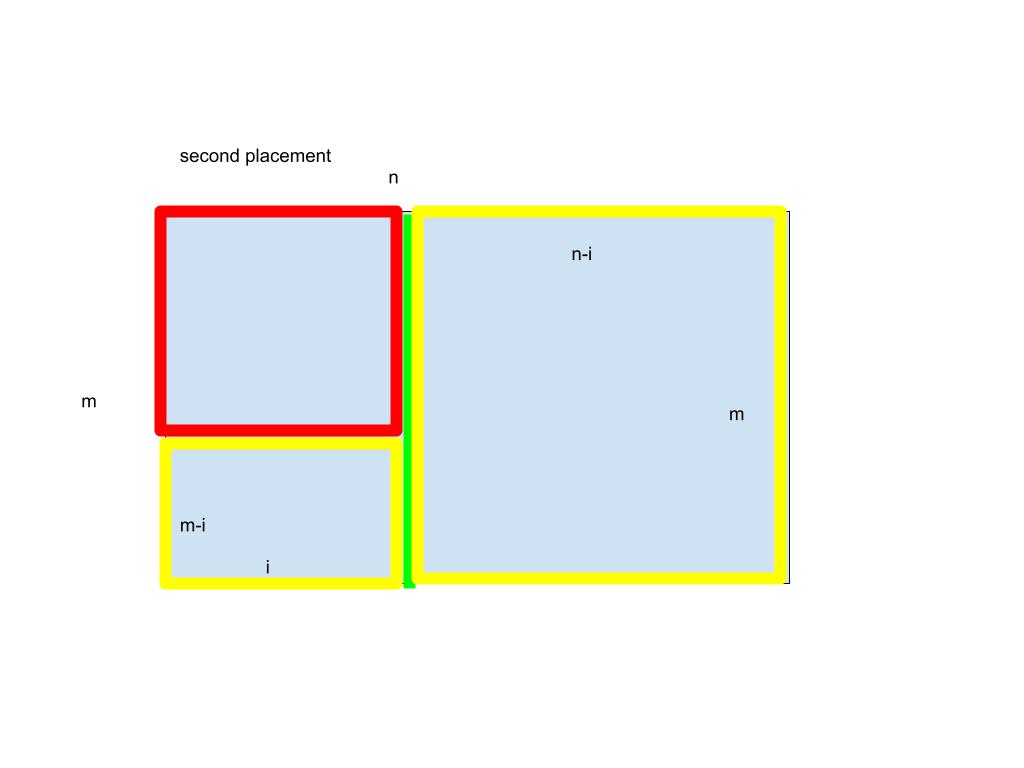
每次从左上角放正方形，然后把剩下的不规则图形分成不同类型的矩形。一共有三种分割方式：
1.
2.
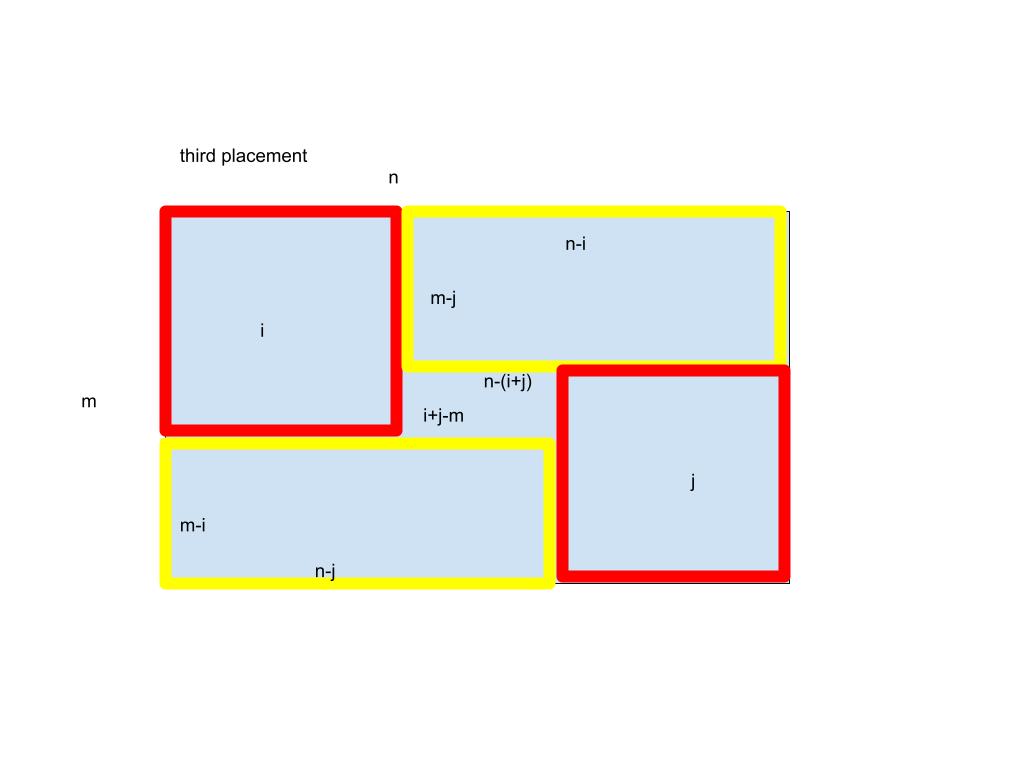
3.

时间复杂度

?

C++ 代码

class Solution {
public:
    int tilingRectangle(int n, int m) {
        if (n > m) return tilingRectangle(m, n);
        vector<vector<int>> memo(n + 1, vector<int>(m + 1));
        return helper(n, m, memo);
    }
    int helper(int n, int m, vector<vector<int>>& memo) {
        if (n > m) return helper(m, n, memo);
        if (n == 0) return 0;
        if (n == m) return 1;
        if (n == 1) return m;
        if (memo[n][m] > 0) return memo[n][m];
        int res = INT_MAX;
        for (int i = 1; i <= n; ++i) {
            res = min(res, 1 + helper(n - i, m, memo) + helper(i, m - i, memo));
            res = min(res, 1 + helper(n, m - i, memo) + helper(n - i, i, memo));
            for (int j = n - i + 1; j < m - i && j < n; ++j) {
                res = min(res, 2 + 
                                helper(n - i, m - j, memo) + 
                                helper(i + j - n, m - i - j, memo) +
                                helper(n - j, m - i, memo));
            }
        }
        return memo[n][m] = res;
    }
};