【例题】 直方图中最大矩形

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：

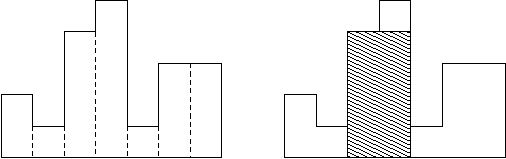
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式

输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数n开始，表示组成直方图的矩形数目。

然后跟随n个整数$h_1，…，h_n$。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为1。

同行数字用空格隔开。

当输入用例为n=0时，结束输入，且该用例不用考虑。

输出格式

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围

$1≤n≤100000$,
$0≤hi≤1000000000$

输入样例：

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

8
4000

单调栈

单调栈顾名思义，就是栈中元素呈现单调性。

插入

将一个元素插入单调栈时，为了维护栈的单调性，需要在保证将该元素插入到栈顶后整个栈满足单调性的前提下弹出最少的元素。

例如，栈中自顶向下的元素为 ，插入元素 时为了保证单调性需要依次弹出元素 ，操作后栈变为 。

用伪代码描述如下：

/*
* 本伪代码对应的是单调递减栈 
*共n个元素，编号为0~n-1
*/
while(栈为空) 栈顶元素出栈; //先清空栈
a[n]=-1;
for(i=0;i<=n;i++)
{
    if(栈为空或入栈元素大于等于栈顶元素) 入栈;
    else 
    {
        while(栈非空并且栈顶元素大于等于入栈元素)
        {
            栈顶元素出栈;
            更新结果; 
        } 
        将最后一次出栈的栈顶元素（即当前元素可以拓展到的位置）入栈; 
        更新最后一次出栈的栈顶元素其对应的值; 
    }    
}
输出结果; 

使用

自然就是从栈顶读出来一个元素，该元素满足单调性的某一端。

例如举例中取出的即栈中的最小值。

题解

其实这是一道贪心+单调栈的题目。

只需要证明所选矩形里面的直方条是单调增的，这时候就变成求单调栈的问题了。其答案就是每次弹出一个高度就计算一下面积，取最大值。

代码演示

//官方标程
#include<iostream>
#include<cstdio>
#include<cstring> 
#include<algorithm>
using namespace std;
int n,p;
int a[100010];
int s[100010],w[100010];
long long ans;

int main()
{
    while(cin>>n&&n)
    {
        ans=0; p=0;
        for(int i=1;i<=n;i++) scanf("%d",&a[i]);
        a[n+1]=0;
        for(int i=1;i<=n+1;i++)
        {
            if(a[i]>s[p]) s[++p]=a[i],w[p]=1;
            else{
                int width=0;
                while(s[p]>a[i])
                {
                    width+=w[p];
                    ans=max(ans,(long long)width*s[p]);
                    p--;
                }
                s[++p]=a[i],w[p]=width+1;
            }
        }
        cout<<ans<<endl;
    }
}