算法提高课汇总

算法思路

$1.$ 输入信息特点是如果不是假话就是真话 — 输入每次给出$x, y$的关系若无冲突, 则默认
为正确信息. 实际操作表现为如果$x, y$在同一集合中, 说明其关系已经给出, 判断是否有
冲突, 否则将$x, y$加入同一集合并维护其相对关系.

$2.$ 带权并查集思想: 将已经确定关系的动物加入同一并查集(同一颗树)中, 用每个动物到
树根的距离维护其相对关系.

$3.$ 相对关系的维护: 如果给出$x-y$的关系与$y-z$的关系, 我们一定能得出$x-z$的关系.
若用$x$到$y$的有向边表示$x$吃$y$的关系, 则$x, y, z$的可能关系可以表示为:

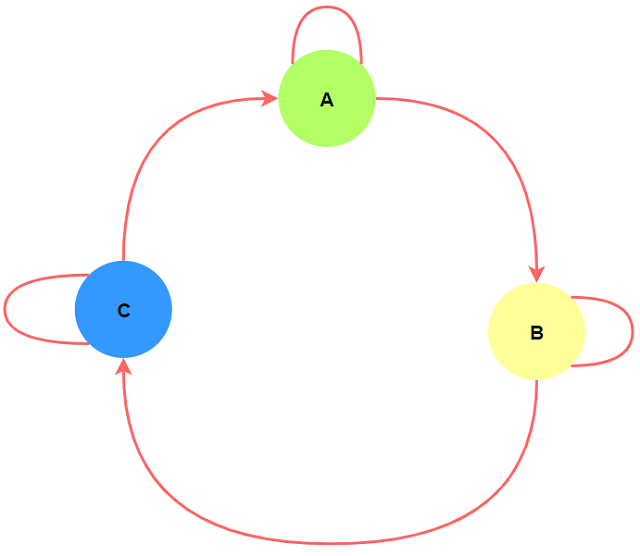
$3.$ 我们可以通过$x\rightarrow y\rightarrow z$间接得到$x-z$的关系.

$4.$ 带权并查集的思想即用根节点作为上述的$y$, 通过根间接得到任意两个动物的关系.

$5.$ 距离: 同一并查集中需要维护三类集合, 用节点到根的距离在模$3$后的数值表示. $\;\;\;\;$(两元素属于同一集合表示其相对关系信息已给出, 距离表示不同类别)

• 0: 该集合中的动物与根同类, 吃集合2.
• 1: 该集合中的动物均吃集合0中的动物.
• 2: 该集合中的动物均吃集合1中的动物.

$\;\;\;\;$ 其中距离的维护与 AcWing 238. 银河英雄传说 类似, $d(x)$表示$x$到其父节点的距离, 在路径压缩过程中将其父节点更新为当前集合的根节点.

具体实现

#include <iostream>

using namespace std;

const int N = 50010;

int n, m;
int p[N], d[N];

int find(int x)
{
    //将p[x]更新为根且更新x到根的距离
    if ( p[x] != x )
    {
        int root = find(p[x]);
        d[x] += d[p[x]];
        p[x] = root;
    }
    return p[x];
}

int main()
{
    cin >> n >> m;

    for ( int i = 1; i <= n; i ++ )
    {
        p[i] = i; 
        //d[i] = 0; 默认动物与自己同类 所以条件3. 与默认信息冲突
        //可与其他情况统一处理
    }

    int res = 0;
    while ( m -- )
    {
        int t, x, y;
        cin >> t >> x >> y;
        if ( x > n || y > n )   res ++ ;
        else
        {
            int px = find(x), py = find(y);
            if ( t == 1 )
            {
                //px == py表示x, y关系已经在之前给出
                if ( px == py && (d[x] - d[y]) % 3 )    res ++;
                else if ( px != py )
                {//加入x, y的关系
                    p[px] = py; //将x, y放入同一集合
                    d[px] = d[y] - d[x];
                    //保证(d[x] + d[ p[x] ] - d[y]) % 3 = 0
                }
            }
            else
            {
                if ( px == py && (d[x] - d[y] - 1) % 3 )    res ++;
                else if ( px != py )
                {
                    p[px] = py;
                    d[px] = d[y] + 1 - d[x];
                    //( d[x] + ? - d[y] )% 3 == 1
                }
            }
        }
    }
    cout << res << endl;

    return 0;
}