算法提高课汇总

算法思路

如果题目只考虑两个战舰是否在同一列中, 可以直接用并查集求解.

在此基础上我们还需考虑两个战舰间隔的距离. 如果直接存储两两战舰的距离,
则至少需要$O(n^2)$的时间. 考虑相对距离的思想: 维护每个元素到集合代表
元素的距离 — 本题中用队头战舰作为代表元素. 则两个元素的距离即两个元素
相对根元素的距离之差.

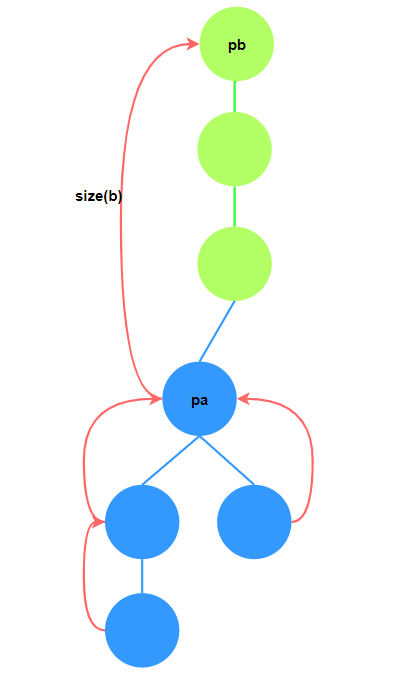
当队列$a$合并至$b$的末尾时, $a$队列中所有战舰到新队头的距离均需要加上
队列$b$的大小. 在实现时, 元素到队头的距离可以用递归思想定义:

• 元素到队头距离 $=$ 元素到其父节点距离 $+$ 父节点到队头距离.

这样做的好处是对于$a$中元素, 其代表元素$pa$是当前$a$中所有元素的公共祖先,
只需更新$pa$到$b$队头的距离, 其余元素在$find$的过程中递归更新.
(类似差分或者线段树懒标记思想).

具体实现

实现时注意题目求的是两个元素的间隔距离而不是距离.

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 30010;

int p[N], d[N], s[N]; 

int find(int x)
{//路径压缩 + 更新x到其队头的距离
    if ( p[x] != x )
    {
        int root = find(p[x]); //路径压缩
        d[x] += d[ p[x] ]; //更新距离
        p[x] = root; //路径压缩
    }
    return p[x];
}

int main()
{
    for ( int i = 1; i < N; i ++ )  
    {
        p[i] = i;
        s[i] = 1;
        //d[i] = 0;
    }

    int m;
    scanf("%d", &m);
    while ( m -- )
    {
        char op[2]; //scanf字符串读入的好处是可以忽略空白字符
        int a, b;
        scanf("%s%d%d", op, &a, &b);
        if ( op[0] == 'M' )
        {
            int pa = find(a), pb = find(b);
            if ( pa != pb )
            {
                d[pa] = s[pb];
                p[pa] = p[pb];
                s[pb] += s[pa];
            }
        }
        else
        {
            int pa = find(a), pb = find(b);
            if ( pa != pb ) puts("-1");
            else    printf("%d\n", max( 0, abs(d[a] - d[b]) - 1 ));
        }
    }
    return 0;
}