如果直接用 前缀和 + 暴力，复杂度将是O($N^4$)，必须优化
优化的方法是：
1）枚举子矩阵的 左边界i 和 右边界j，
2）用 快指针t 枚举 子矩阵的下边界，慢指针s 维护 子矩阵的上边界 (s $\le$ t)
3）如果得到的子矩阵的权值和 大于 k，则慢指针s 前进，而子矩阵和必将单调不增
4）慢指针s 继续前进（如图），直到 子矩阵的和 不大于k，慢指针没必要前进了，因为该子矩阵的所有宽度为 j - i + 1 的子矩阵（总共 t - s + 1 种）一定满足要求，更新该情况对答案的贡献 t - s + 1；反之，如果慢指针s越界（s > t），则不操作，直接进入下层循环
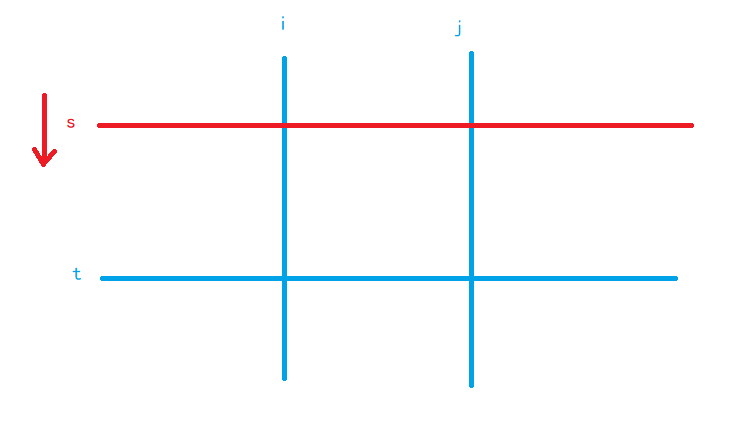
复杂度：O($N^3$)
代码如下：
#include<iostream>
using namespace std;
typedef long long ll;
const int N = 5e2+3;
int n, m, k;
int a[N][N];
int main(){
ios::sync_with_stdio(false);
cin >> n >> m >> k;
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
cin >> a[i][j];
a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
}
}
ll ans = 0;
for(int i=1; i<=m; i++){
for(int j=i; j<=m; j++){
for(int s = 1, t = 1; t <= n; t ++ ){
while(s <= t && a[t][j] - a[s - 1][j] - a[t][i - 1] + a[s - 1][i - 1] > k) s ++ ;
if(s <= t) ans += t - s + 1;
}
}
}
cout << ans << '\n';
}
给大佬加个解释，$t-s+1$ ：代表左边界为 $i$，右边界为 $j$，且包含 $s$ 这条线的的所有满足条件的子矩阵个数为 $t-s+1$ 。为何这样定义，可以理解为 $s$ 这条线在 $(i,j)$ 固定下是具有唯一性的(当然这难免有点为了理解而去解释)。
佬 就找你这个解释呢
赞一个
前排提示，前缀和数组别开longlong，这卡常卡的太tm极限了
不是很懂，为啥啊
在64系统下，long long 和 long 一般占8个字节，int 占4个字节，开的太大容易没内存。
while(s <= t && a[t][j] - a[s - 1][j] - a[t][i - 1] + a[s - 1][i - 1] > k) s ++ ; if(s <= t) ans += t - s + 1;我看了好一会，才看懂，上边界移动的条件，是上下区间和大于指定元素，此时我们需要收缩上边界，后面t - s + 1 我一开始觉得这里面应该写出++，每次加1，后来一项，这里面的区间都是符合条件的，而且是唯一的，这里需要想明白
二维vector会TLE
stl太慢了
大佬们，为什么要加一个1
不能是t-s？
因为是双闭区间，如果你严格定义s<t，上闭下开区间就不用+1
为什么要加1啊，当s=t时，就不是矩阵了，不满足条件了，答案为什么要算s=t这种情况啊？
1x1也是矩阵
擦，大哥
666
while(s <= t && a[t][j] - a[t - s][j] - a[t][j - i] + a[t - s][j - i] > k) s ++; 这样写为什么不对啊
我觉得应该是有s=t这个条件会使得t-s=0
去复习二维前缀和吧、
为什么是i<=m啊
因为i和j分别是一行中的左边界和右边界
orz
ORZ
### 感谢分享
tql
大哥，牛，真牛，啥也不说了，点赞，扣666
好好好，一看图就懂了
666666666666
比y总那个看的舒服
6666666666666
tql,秒懂
外面两层循环为啥不加括号就tle了
原来是卡常
为啥括号还能导致卡常啊
同问