高斯消元解线性方程组的最后一步是倒着推出答案，但是这个比较抽象，所以手动模拟了一下样例（字儿丑不要介意）：

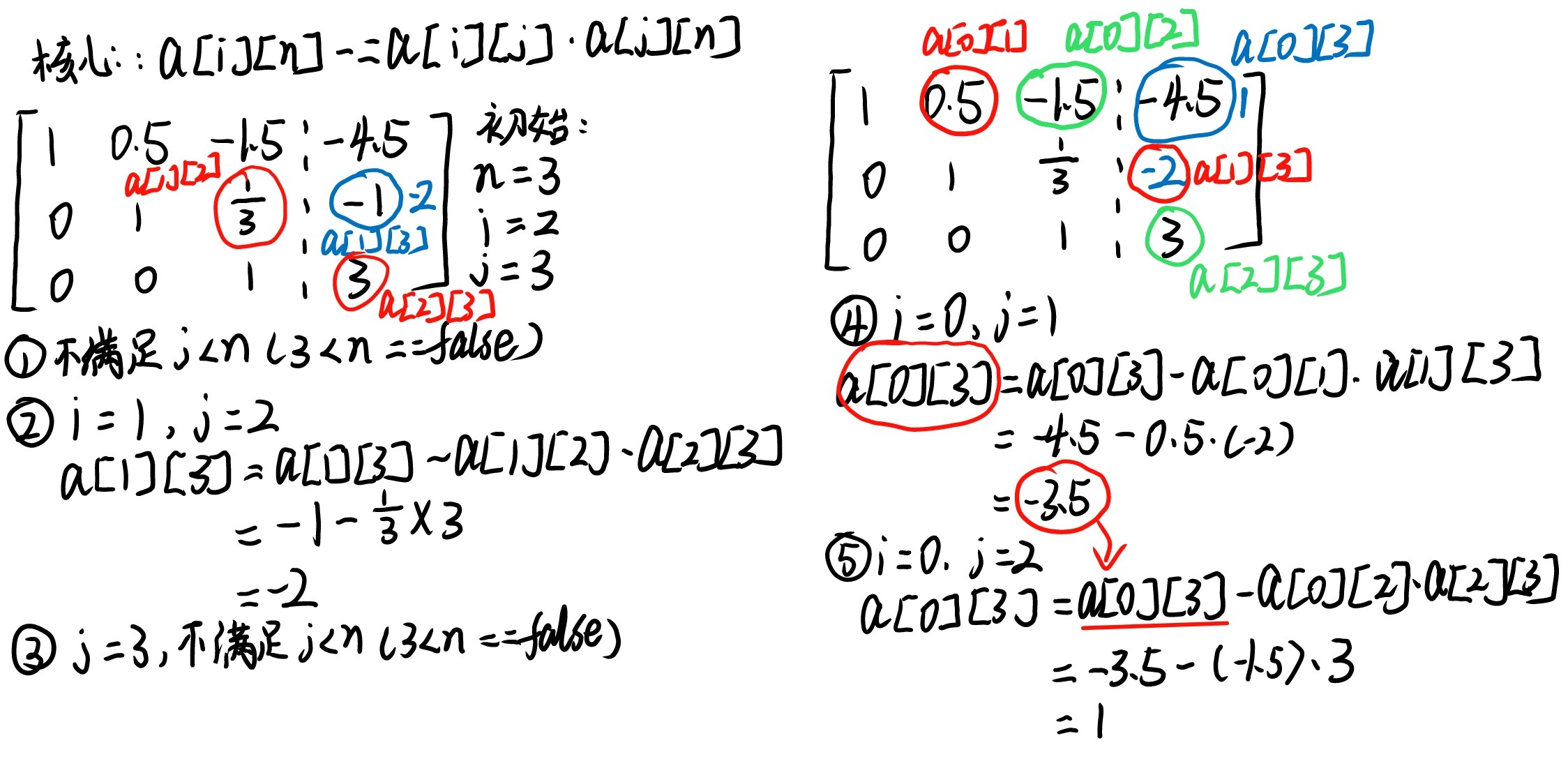
因此，可以发现这一步骤的核心思路是：从倒数第二行开始，动态更新最后一列，使之从常数 $b$ 变为某一行所对应的 $x$（例如，第二行代表 $x_2$，也就是 a[1][n]）。P.S. 从倒数第二行开始是因为最后一行对应的 $x$ 已知。

但是具体是怎么更新的呢？可以发现，例如对于 $x_2$ 来说，有 $1\cdot x_2 + \frac{1}{3}\cdot x_3 = -1$，移向得 $x_2 = -1 - \frac{1}{3}\cdot x_3$。又 $x_3 = 3$，因此得 $x_2 = -2$，储存在 a[1][n] 中（对于数组来说，是从 [0][0] 开始的，所以不要搞混）。

但是，为什么 $i$ 和 $j$ 就这么巧合地使上式成立了？因为到最后一步之前，如果没有 return，那么整个系数矩阵已经变成了主对角线（“\”）都为 1 的阶梯型矩阵（也就是有唯一解），因此，观察易得 每一行的行数 + 1 一定是 1 后面的第一个数。例如：第二行的行数 2 + 1 == 3，第二行第三个数是 1 后面的第一个数。

这样的话，i 代表一行，固定不变；j = i + 1，从 1 后面的第一个数开始。

这就代表着，只要可以再给它们（1 后面的数）乘上它们所对应的 $x$，并从当前行的常数 $b$（例如上面 $1\cdot x_2 + \frac{1}{3}\cdot x_3 = -1$ 中的 $-1$） 中减去它们的乘积，就得到了当前行所对应的 $x$（或者说当前行的 1 所代表的那个 $x$）。

此时，又有一件很巧妙的事情出现了：我们的变量 j 不仅能代表列，还能和 n 一起代表 $x_{n+1}$（加一是因为数组是从 [0][0] 开始的），因为题目保证了所给的矩阵是一个方阵！

因此，如果有唯一解，只需要输出 a[i][n](for(int i = 0; i < n; i++)) 即可。