<— 麻烦点一下旁边那个向上的三角

图片建议点开查看

推销一下：

$\color{#00FF7F}{算法提高课 第一章 动态规划 全题解（正在完善）}$

题目描述

小明手里有$n$元钱全部用来买书，书的价格为$10$元，$20$元，$50$元，$100$元。

问小明有多少种买书方案？（每种书可购买多本）

输入格式

一个整数 $n$，代表总共钱数。

输出格式

一个整数，代表选择方案种数。

数据范围

$0≤n≤1000$

输入样例1：

20

输出样例1：

2

输入样例2：

15

输出样例2：

0

输入样例3：

0

输出样例3：

1

题意简化：

小明手里有$n$元钱全部用来买书，每种书的价格为$10$元，$20$元，$50$元，$100$元。

问小明有多少种买书方案？（每种书可购买多本）

算法1

(二维数组DP) $O(n^3)$

这道题与 AcWing 278. 数字组合 比较相似，都是求方案数量。

注意到每种书可购买无数本，可以判断为完全背包求方案数量问题。

那我们根据 01背包求方案数量问题 的经验，可以知道，我们把属性改为 $Count$，计算方法改为累计方案数量即可。

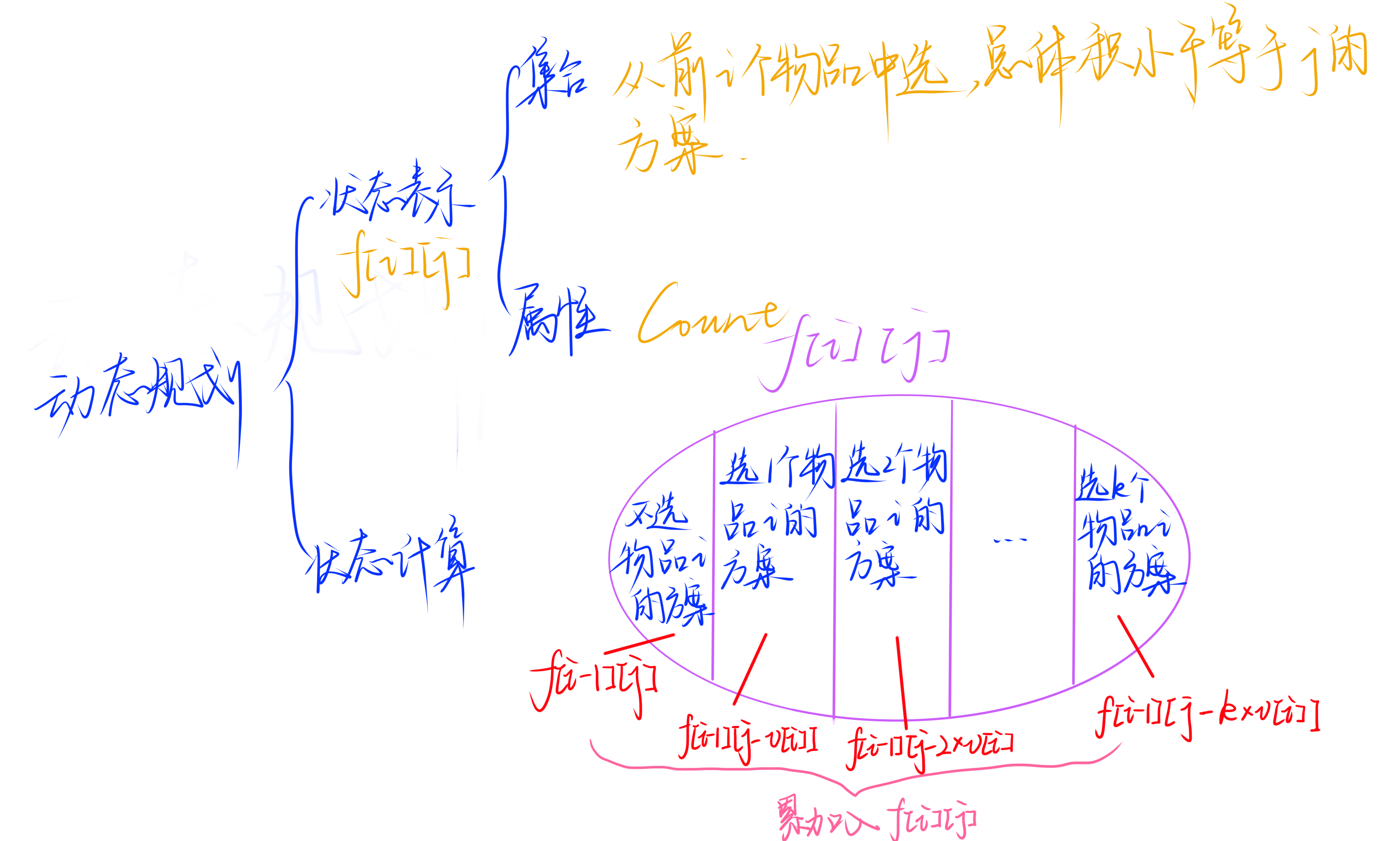
如果你还不知道完全背包的话，可以看一下我的题解

$$（注意此为三重循环未优化版本）$$

时间复杂度

参考文献

C++ 代码

#include <iostream>
using namespace std;
const int N = 1010;
int v[N] = {0,10,20,50,100};
int f[N][N];
int main(){
    int n = 4,m;
    scanf("%d",&m);
    f[0][0] = 1;
    for(int i = 1;i <= n;i ++){
        for(int j = 0;j <= m;j ++){
            for(int k = 0;v[i] * k <= j;k ++){
                f[i][j] += f[i - 1][j - v[i] * k];
            }
        }
    }
    printf("%d",f[n][m]);
    return 0;
}

这题数据很小，就过了，但是我们可以优化一下代码

算法2

(完全背包—经典优化) $O(n^2)$

f[i][j]   =    f[i - 1][j] + f[i - 1][j - v * 1] + f[i - 1][j - v * 2] + ... + f[i - 1][j - v * s]
f[i][j - v] =                f[i - 1][j - v * 1] + f[i - 1][j - v * 2] + ... + f[i - 1][j - v * s]

我们发现，对齐的部分完全一样
所以，我们可以得出状态转移方程：
$$f[i][j] = f[i − 1][j] + f[i][j − v_i]$$

时间复杂度

现在优化掉了一层，$O(n ^ 2)$

参考文献

C++ 代码

#include <iostream>
using namespace std;
const int N = 1010;
int v[N] = {0,10,20,50,100};
int f[N][N];
int main(){
    int n = 4,m;
    scanf("%d",&m);
    f[0][0] = 1;
    for(int i = 1;i <= n;i ++){
        for(int j = 0;j <= m;j ++){
            f[i][j] = f[i - 1][j]; //不选
            if(j >= v[i]) f[i][j] += f[i][j - v[i]]; //选
        }
    }
    printf("%d",f[n][m]);
    return 0;
}

算法3

(一维动态规划) $O(n^2)$

我们现在可以按照01背包的优化方案来把$f$数组优化为一维的

时间复杂度

参考文献

C++ 代码

#include <iostream>
using namespace std;
const int N = 1010;
int v[N] = {0,10,20,50,100};
int f[N];
int main(){
    int n = 4,m;
    scanf("%d",&m);
    f[0] = 1; // 原因是不选也是一种方案
    for(int i = 1;i <= n;i ++){
        for(int j = v[i];j <= m;j ++){
            f[j] += f[j - v[i]];
        }
    }
    printf("%d",f[m]);
    return 0;
}

（共180行）