<---- 麻烦点一下旁边那个向上的三角

推销一下：

$\color{#00FF7F}{算法提高课 第一章 动态规划 全题解（正在完善）}$

题目描述

给你一个$n$种面值的货币系统，求组成面值为$m$的货币有多少种方案。

输入格式

第一行，包含两个整数$n$和$m$。

接下来$n$行，每行包含一个整数，表示一种货币的面值。

输出格式

共一行，包含一个整数，表示方案数。

数据范围

$n≤15,m≤3000$

输入样例：

3 10
1
2
5

输出样例：

10

题意简述

给定 $n$ 种面值的货币，求组成面值为 $m$ 的货币有多少种方案。

注意：

每种面值的货币可以重复使用
每种方案必须是组成的面值恰好等于$m$
求的是方案数量，不是最大价值

算法1

(二维动态规划) $O(n^3)$

这道题只要抽象好表述，就能很快与 AcWing 1023. 买书 一题对应，从而快速解决问题。

根据

组成面值为 $m$ 的货币
可以感受到，可以将 $m$ 抽象为背包容量。
那物品是什么呢，除了 $m$ 只剩下 $n$ 种面值的货币。
那我们将其抽象为物品体积，并将物品放入背包，求方案数。

整理：

• 组成面值为 $m$ 的货币 $\to$ 背包容量
• $n$ 种面值的货币 $\to$ 物品体积

求方案数量我们可以参考最初的 AcWing 278. 数字组合 01背包求方案数量问题。

注意到隐藏条件：货币有无数张。可以判断为完全背包求方案数量问题。

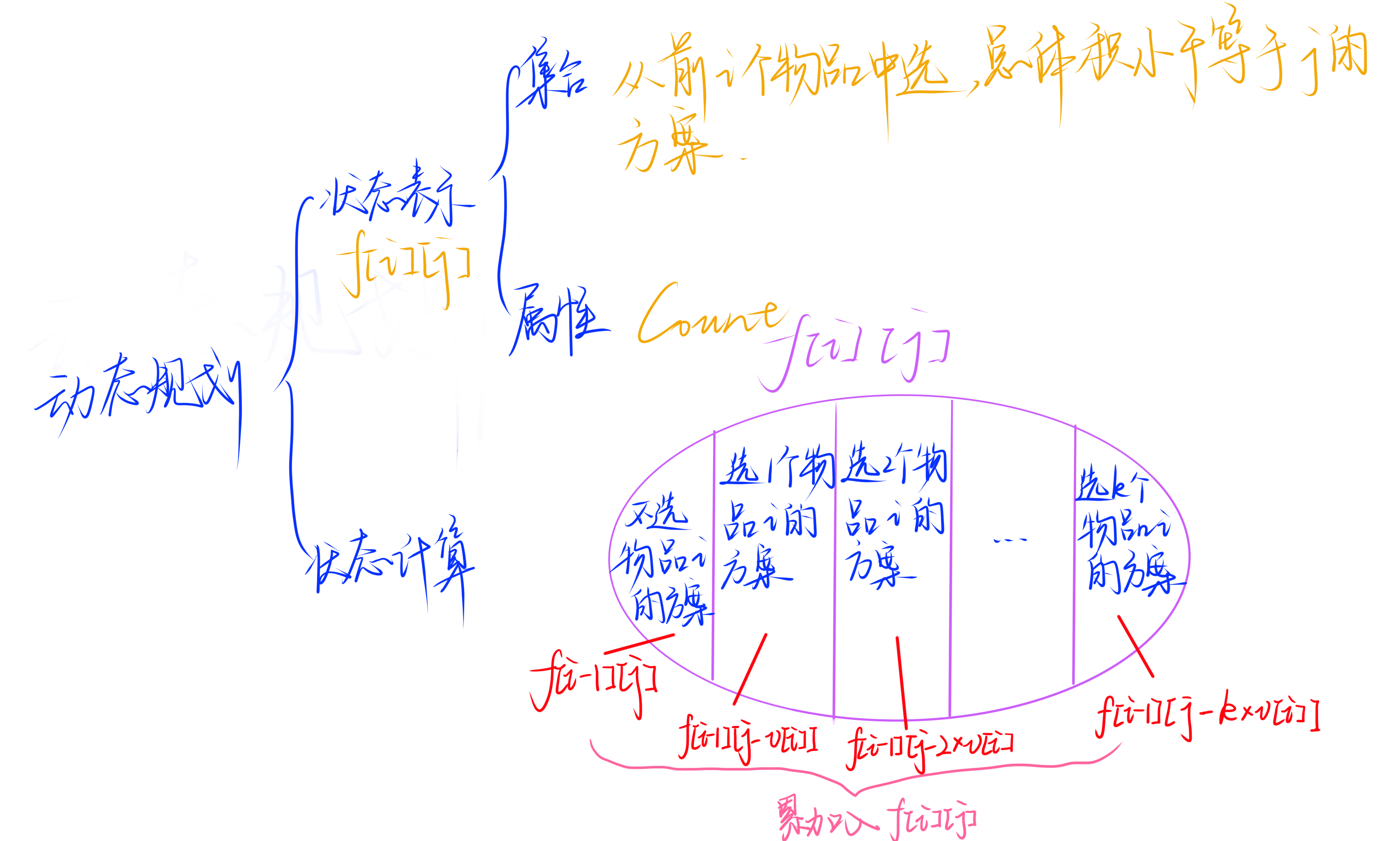
时间复杂度

参考文献

C++ 代码

#include <iostream>
using namespace std;
const int N = 3010;
int v[N];
long long f[N][N];
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    f[0][0] = 1;
    for(int i = 1;i <= n;i ++) scanf("%d",&v[i]);
    for(int i = 1;i <= n;i ++){
        for(int j = 0;j <= m;j ++){
            for(int k = 0;v[i] * k <= j;k ++){
                f[i][j] += f[i - 1][j - v[i] * k];
            }
        }
    }
    printf("%lld",f[n][m]);
    return 0;
}

注意：

这里的 $f$ 数组会爆 $int$，所以要用$long \ long$
如果你是用 $printf$ 输出，记得是printf("%lld",f[n][m])

算法2

(一维数组DP) $O(n^2)$

这里我就只把最初和最后的代码放出来啦，其他方法可以看一下我买书那题的题解

时间复杂度

参考文献

C++ 代码

#include <iostream>
using namespace std;
const int N = 3010;
int v[N];
long long f[N];
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    f[0] = 1;
    for(int i = 1;i <= n;i ++) scanf("%d",&v[i]);
    for(int i = 1;i <= n;i ++){
        for(int j = v[i];j <= m;j ++){
            f[j] += f[j - v[i]];
        }
    }
    printf("%lld",f[m]);
    return 0;
}

$$（共140行）$$