原题链接
更好的阅读体验

题目描述

假设海岸是一条无限长的直线，陆地位于海岸的一侧，海洋位于另外一侧。

每个小岛都位于海洋一侧的某个点上。

雷达装置均位于海岸线上，且雷达的监测范围为d，当小岛与某雷达的距离不超过d时，该小岛可以被雷达覆盖。

我们使用笛卡尔坐标系，定义海岸线为x轴，海的一侧在x轴上方，陆地一侧在x轴下方。

现在给出每个小岛的具体坐标以及雷达的检测范围，请你求出能够使所有小岛都被雷达覆盖所需的最小雷达数目。

输入格式
第一行输入两个整数n和d，分别代表小岛数目和雷达检测范围。

接下来n行，每行输入两个整数，分别代表小岛的x，y轴坐标。

同一行数据之间用空格隔开。

输出格式
输出一个整数，代表所需的最小雷达数目，若没有解决方案则所需数目输出“-1”。

数据范围
$1≤n≤1000$

样例

输入样例：
3 2
1 2
-3 1
2 1
输出样例：
2

贪心+排序

首先这道题目我们第一个要做的,就是将这个笛卡尔坐标系,转化为区间.那么我们怎么做才能让这道题目转换为区间呢?看一下下图你就会知道怎么做了.

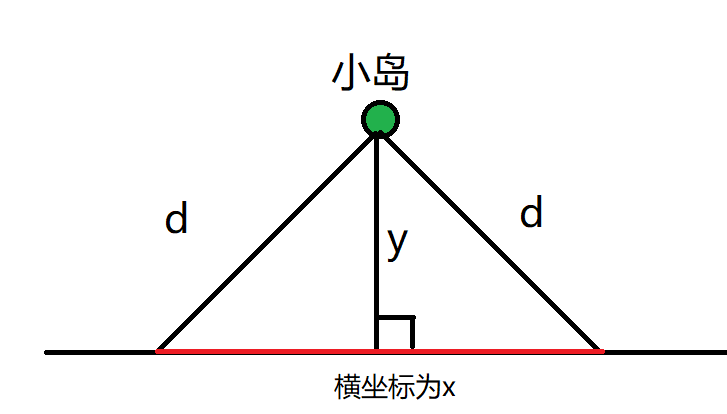
对于上面这个图片的小岛而言,它可以被雷达搜索到,只有当他的x坐标在红线区域才会被搜索到.当然y坐标也不能够太大了,如果太大了那么肯定是无解的情况.

那么我们如果计算这个红线覆盖区域呢,你会发现上面的图片是由两个直角三角形构成的,而且知道两条边,那么根据勾股定理我们自然就可以求出第三边.公式如下图所示

y=abs(y);//因为y坐标有可能在x轴下面.
if (y>d)//肯定无法搜索到了
{
    puts("-1");
    return 0;
}
a[i].l=x-sqrt(d*d-y*y);//红线的开头
a[i].r=x+sqrt(d*d-y*y);//红线的结尾

现在我们发现,这道题目已经变成了区间覆盖问题,问至少要多少个雷达才能覆盖完这些区间,那么对于每一条红线而言,如果当前的雷达都无法搜索到它,那么必然需要新增一个雷达去找到它.

因为我们可以将所有区间都排个序,也就是按照每条线的终点坐标从小到大排序,那么我们只需要保存最近的雷达,如果说这个最近的雷达都无法访问这座小岛,那么我们就可以在a[i].r的位置上开辟一个新的雷达.

也就是在可以覆盖这座小岛的最后一个点.这就是我们贪心的策略,因为很明显a[i].r这个位置比前面那些点放置雷达,可以覆盖的位置更多.

记得要用double类型,不然你会WA掉的

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e4;
struct node
{
    double l,r;
    friend bool operator <(node a,node b)//内嵌排序,其实就是cmp.
    {
        return a.r<b.r;
    }
} a[N];
int n,m,i,j,k,d,vis[N],ans;
int main()
{
    cin>>n>>d;
    for(int i=1;i<=n;i++)
    {
        int x,y;
        cin>>x>>y;
        y=abs(y);
        if (y>d)
        {
            puts("-1");
            return 0;
        }
        a[i].l=x-sqrt(d*d-y*y);
        a[i].r=x+sqrt(d*d-y*y);
        vis[i]=false;
    }
    sort(a+1,a+1+n);
    for(int i=1;i<=n;i++)
    {
        if (!vis[i])//这个点没有被选中
        {
            ans++;//新增了一个雷达.
            vis[i]=true;
            for(int j=i+1;j<=n;j++)//判断这个雷达,可以覆盖后面那些小岛
                if (a[j].l<=a[i].r)
                    vis[j]=true;
        }
    }
    cout<<ans;
    return 0;
}