👈 制作不易，轻点资瓷！

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $

$\Huge\color{green}{春季每日一题2022题解集合}$

$\color{SteelBlue}{注意了！我是第一个写这题题解的人！！！}$

还不点赞？！

为了精简这个过程，他制造了一个伟大的发明：便便传送门！

伟大的发明

思路

我一开始看到这题，第一反应：分类讨论！（话说我是不是中毒了，啥都是分类讨论）

后来在写代码的过程中发现，好像没那么烦

接下来我就讲讲我的史上最简单易懂的思路

我想有人可能已经看了我的代码，非常简短

的确，这题我们只需比较走传送门的距离小还是不走传送门的距离小就行了

先上图！

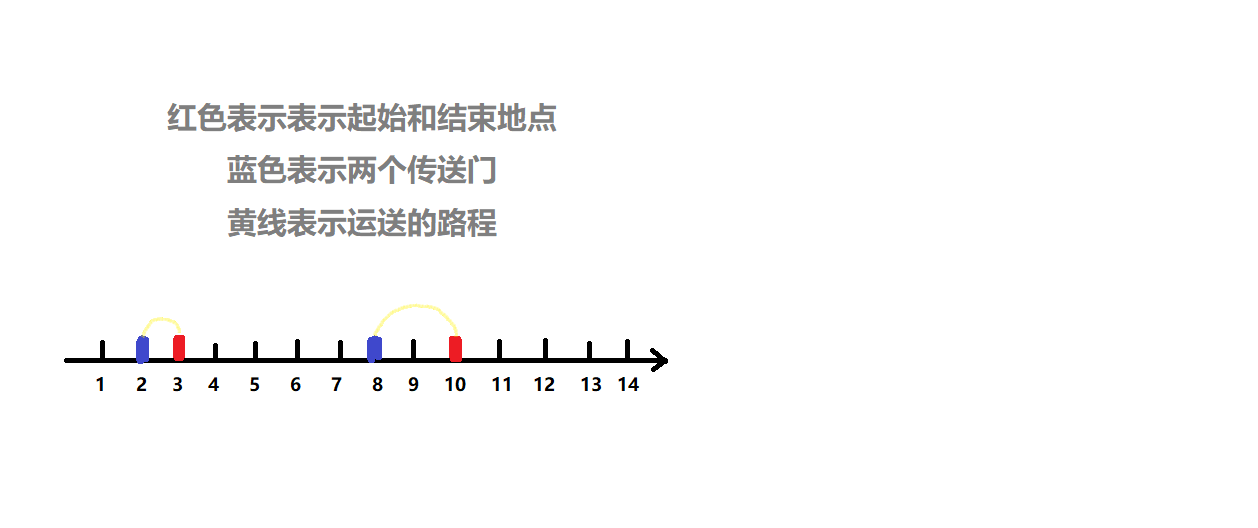
为了防止出现负数，我们使用 $abs$

那么走传送门的距离就是 $\ \ $ $abs(min(a,b)-min(x,y))+abs(max(a,b)-max(x,y))$

（起点到一个传送门的距离 + 终点到另一个传送门的距离）

不走传送门的距离………就直接 $\ \ $ $abs(a-b)$

最后输出两个距离中小的那个~

哎呀，不知不觉已经把重要代码给你们了

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $

C++ 代码

#include<bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;
int a,b,x,y,ans=0; 
int main(){
    scanf("%d%d%d%d",&a,&b,&x,&y);
    int d1=abs(min(a,b)-min(x,y))+abs(max(a,b)-max(x,y));
    int d2=abs(a-b);
    cout<<min(d1,d2);
    return 0;
}

还有不懂的扣在评论区~~