算法
(贪心) O(nlogn)
如下图所示,对于任意一个小岛 (x,y),我们都可以在海岸线上求出能覆盖该小岛的建造雷达的区间 [a,b]。
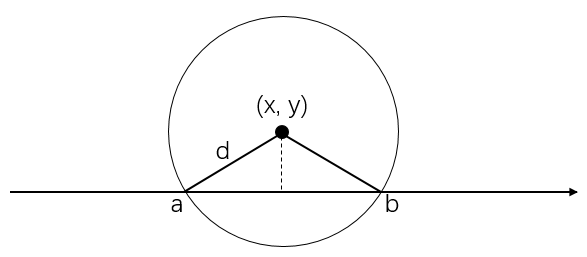
由勾股定理可知:
- a=x−√d2−y2;
- b=x+√d2−y2;
将所有小岛转化成区间后,问题转化为:给定 n 个区间,在 x 轴上选择尽量少的点,使得所有区间至少包含一个点。
我们先给出做法,再证明其正确性。
算法步骤:
- 将所有区间按右端点从小到大排序;
- 依次考虑每个区间:
- 如果当前区间包含最后一个选择的点,则直接跳过;
- 如果当前区间不包含最后一个选择的点,则在当前区间的右端点的位置选一个新的点;
证明:
首先上述做法一定可以保证所有区间都至少包含一个点。
然后我们再证明这样选出的点的数量是最少的,不妨设选出的点数是 m:
- 按照上述做法,我们选择的点都是某个区间的右端点,而且由于区间按右端点排好序了,所以我们选择的点也是排好序的;
- 只有在当前区间和上一个点所对应的区间是没有交集时,我们才会选择一个新点,所以所有选出的点所对应的区间是如下图所示的情况,两两之间没有交集。

所以我们找到了 m 个两两之间没有交集的区间,因此我们至少需要选 m 个点。而且通过上述做法,我们可以只选 m 个点。因此最优解就是 m。
时间复杂度
- 计算每个坐标所对应的区间,需要 O(n) 的计算量;
- 将所有区间排序需要 O(nlogn) 的计算量;
- 扫描所有区间需要 O(n) 的计算量;
所以总共的时间复杂度是 O(nlogn)。
C++ 代码
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
typedef pair<double, double> PDD;
const int N = 1010;
const double eps = 1e-6, INF = 1e10;
int n, d;
PDD seg[N];
int main()
{
cin >> n >> d;
bool success = true;
for (int i = 0; i < n; i ++ )
{
int x, y;
cin >> x >> y;
if (y > d)
{
success = false;
break;
}
auto len = sqrt(d * d - y * y);
seg[i] = {x + len, x - len};
}
if (!success) puts("-1");
else
{
sort(seg, seg + n);
int res = 0;
double last = -INF;
for (int i = 0; i < n; i ++ )
{
if (seg[i].second > last + eps)
{
res ++ ;
last = seg[i].first;
}
}
cout << res << endl;
}
return 0;
}


有一说一 这里y总的证明和思路都 > 蓝书
我也是博采众家之长hh
y总 可以出书了。
雀食
y总,为啥不能是按左端点排序啊
y总这个pair是按照终点排序,如果用左端点排序是要重写小于号,我刚转明白
两种排序方法只会导致一种情况不同:假如a是-2到2,b是-1到1,按右端点排序先看b
再看a,此时last在1,也就是插在1的位置,1也是在a的区间内;而按左端点是先看a,到判断b时直接跳过去了,但此时last是插在2,也就是a的右端点,此时雷达已经超出了b的范围。所以右端点从小到大是确保当前插下的雷达一定在所有区间内。
都可以,问题的重点是只有在当前区间与上一个取点的区间完全不相交时才取新的点,这样才能使取得点数量最小,排序只是会使取点的策略不同而已。
直接sort不是按左端点排序吗?
pair的第一关键字存的是右端点。
按照左端点排序的代码,对pair顺序稍加改变,另外需要更新last
#include <cstring> #include <iostream> #include <algorithm> #include <cmath> using namespace std; typedef pair<double, double> PDD; const int N = 1010; const double eps = 1e-6, INF = 1e10; int n, d; PDD seg[N]; int main() { cin >> n >> d; bool success = true; for (int i = 0; i < n; i ++ ) { int x, y; cin >> x >> y; if (y > d) { success = false; break; } auto len = sqrt(d * d - y * y); seg[i] = {x - len, x + len}; } if (!success) puts("-1"); else { sort(seg, seg + n); int res = 0; double last = -INF; for (int i = 0; i < n; i ++ ) { if(last > seg[i].second) last = seg[i].second; // 如果遇到包含在上一区间的更小区间,将last更新 if (seg[i].first > last + eps) { res ++ ; last = seg[i].second; } } cout << res << endl; } return 0; }可参考楼上xd的画的图
究竟需不需要加eps处理呢
这题加不加都可以。
为啥不能直接贪心当前点的最右端,然后跳到下一个尚未被覆盖的点啊
做法不唯一,但每个做法最好想办法证明其正确性。
这题根据左端点和右端点排序分别会造成什么效果呢
根据右端点排序根据上述的证明可以保证选出的点数是最少的。根据左端点排序就要看后续的操作是啥了。
额 进阶指南上确实取了个min
左右是对称的,如果按左端点排序,后续的操作也对称一下就好了
因为你按照左断点再这么做的话,都无法保证每个区间里至少有一个点。如果你非要按照左端点排序,那么至少要从右边开始向左判断左端点。将第一个左端点当作区间最后一个点,往左遍历,如果当前区间不包含这个点,ret++,并且将这个新区见的左端点作为新的最后一个点。
确实。我开始按照左端点排序从左向右遍历时答案偏小。应该从右边开始向左遍历

图画的很好理解,感谢!
从左往右时,last要取个min
左端点排序没有问题!你这出错是因为你没有考虑每遍历一个区间就要维护一次最小值!
按左端点排序的话,last要取个min,而按右端点排序可以省略这一步骤
为啥不能按x排序 用倍增的思想取出一段区间 check判断这段区间x【mid】是否满足d范围条件 满足就倍增 不满足就回退
“覆盖所有区间的最少点数”
请问为什么不可以算:直线距离<= 2 * r那么贪啊,或者是按x与x +1的距离,我觉得这样非常有道理啊
pair<double, double> p[1005]; int n, r; bool check(pair<double, double> a, pair<double, double>b){ double temp = (a.first - b.first) * (a.first - b.first) ;////直线距离只过-1的样例, 这样写只过四个样例 if(temp <= 2 * r) return true; return false; } int main() { IOS; // freopen("P1908_6.in","r",stdin);//读入数据 // freopen("P1908.out","w",stdout); //输出数据 cin >> n >> r; for (int i = 0; i < n; ++i){ cin >> p[i].first >> p[i].second; if(abs(p[i].second) > r) { cout << -1; return 0; } } sort(p, p + n); // for(int i = 0; i < n; ++i) cout << p[i].first << ' ' << p[i].second << endl; int ans = 0; for (int i = 0; i < n;){ int j = i; while(check(p[i], p[j]) && j < n){ ++j; } i = j; ++ans; } cout << ans; return 0; }而且如果最大以2R贪,他的长度还更大了。本来就必须在海岸线上,那就是把一个圆分成两半,就是2R啊
想问下pair第二关键字怎么直接排序呀,我是把区间的左右互换了😂
就是这样
写个bool cmp() return a.y < b.y
最后一个选择的点....原来是上一个选择的点 看了代码才知道
请问比较函数为什么不可以是“先比较L端点,从小到大排序,如果相等比较右端点,右端点大的在前面”。我觉得可以啊
if(x.l<y.l) return true; else if (x.l>y.l) return false; else{ if(x.r>y.r) return true; else return false; }这个证明可以
就很严谨。
这道题如果按照左端点排序 然后倒序遍历 如果当前区间与前面的区间有交集就为一个监控 如果没有交集就新建监控
上面这种策略好像会wa掉两个点 是为什么呢
这种做法和上述做法是对称的,算法本身应该没问题,可能是代码写错了。
对的 确实是我当时代码写错了 谢谢老师!
好滴,客气啦