算法提高课汇总

算法思路

为求解答案我们需要枚举所有$n\times n$正方形中 $maxv-minv$ 的值, 但直接处理
二维数组比较困难.

考虑一种求最值降维方式, 以求最大值为例: 先按行预处理数组$row_{ij}$, $row_{ij}$表示
下标从$(i, j-n+1)\sim (i, j)$元素的最大值.

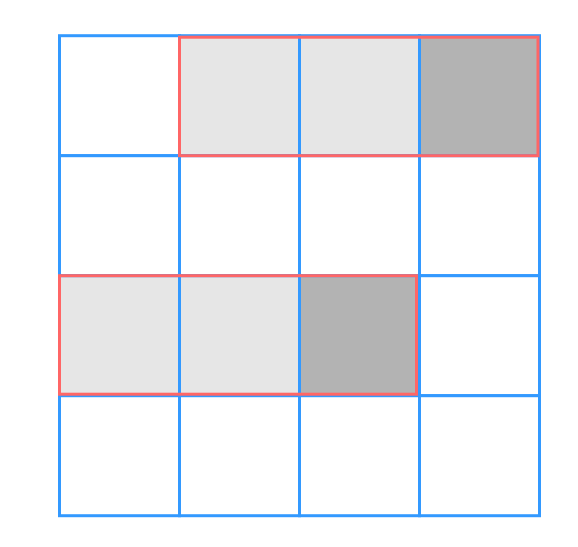
当我们求某$n\times n$正方形中的最大值时, 只需求最右侧列最值即可.

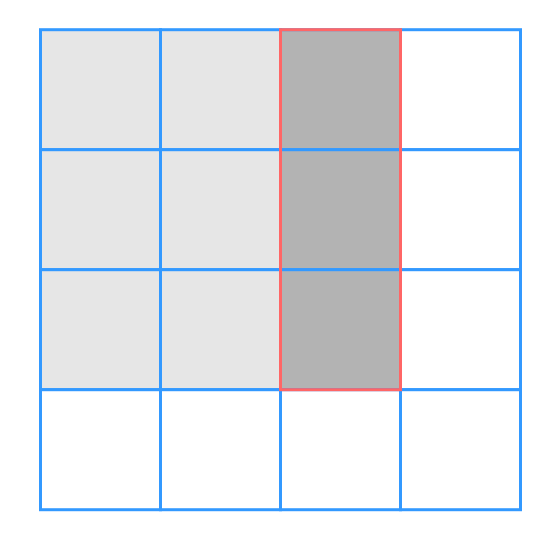
通过这种方式我们2次求解一维数组最值 — 单调队列优化, 而不需要直接求解二维数组最值.

代码实现

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, INF = 0x3f3f3f3f;

int n, m, k;
int w[N][N];
int row_max[N][N], row_min[N][N]; 
int q[N];

void get_max(int a[], int b[], int len)
{
    int hh = 0, tt = -1;
    for ( int i = 1; i <= len; i ++ )
    {
        if ( hh <= tt && q[hh] < i - k + 1 )    hh ++;
        while ( hh <= tt && a[q[tt]] <= a[i] )  tt --;
        q[++ tt] = i;
        b[i] = a[q[hh]];
    }
}

void get_min(int a[], int b[], int len)
{
    int hh = 0, tt = -1;
    for ( int i = 1; i <= len; i ++ )
    {
        if ( hh <= tt && q[hh] < i - k + 1 )    hh ++;
        while ( hh <= tt && a[q[tt]] >= a[i] )  tt --;
        q[++ tt] = i;
        b[i] = a[q[hh]];
    }
}

int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for ( int i = 1; i <= n; i ++ )
        for ( int j = 1; j <= m; j ++ )
            cin >> w[i][j];

    for ( int i = 1; i <= n; i ++ )
    {
        get_max(w[i], row_max[i], m); //预处理i行最值 放入最右侧元素中
        get_min(w[i], row_min[i], m);
    }

    int res = INF;
    int a[N], b[N], c[N]; //辅助数组 保存某行中列元素最值

    for ( int j = k; j <= m; j ++ ) //处理j列
    {
        for ( int i = 1; i <= n; i ++ ) a[i] = row_max[i][j]; //先存储j列元素
        get_max(a, b, n);

        for ( int i = 1; i <= n; i ++ ) a[i] = row_min[i][j];
        get_min(a, c, n);

        for ( int i = k; i <= n; i ++ ) 
        {
            //此时b[i]表示以(i, j)作为右下角的正方形元素中的最大值
            //所以(i, j)作为右下角坐标需要从k开始
            res = min(res, b[i] - c[i]);
        }
    }
    printf("%d\n", res);

    return 0;
}