$\color{green}{<–画图不易，点下这里赞一下吧}$

迪杰斯特拉算法不能用于带负权边。

原因： 为什么迪杰斯特拉算法不能用于带负权边 ，最下面有图解。

spfa 算法思路

明确一下松弛的概念。

• 考虑节点u以及它的邻居v，从起点跑到v有好多跑法，有的跑法经过u，有的不经过。

• 经过u的跑法的距离就是distu+u到v的距离。

• 所谓松弛操作，就是看一看distv和distu+u到v的距离哪个大一点。

• 如果前者大一点，就说明当前的不是最短路，就要赋值为后者，这就叫做松弛。

spfa算法文字说明：

• 建立一个队列，初始时队列里只有起始点。

• 再建立一个数组记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。

• 再建立一个数组，标记点是否在队列中。

• 队头不断出队，计算始点起点经过队头到其他点的距离是否变短，如果变短且被点不在队列中，则把该点加入到队尾。

• 重复执行直到队列为空。

• 在保存最短路径的数组中，就得到了最短路径。

spfa 图解：

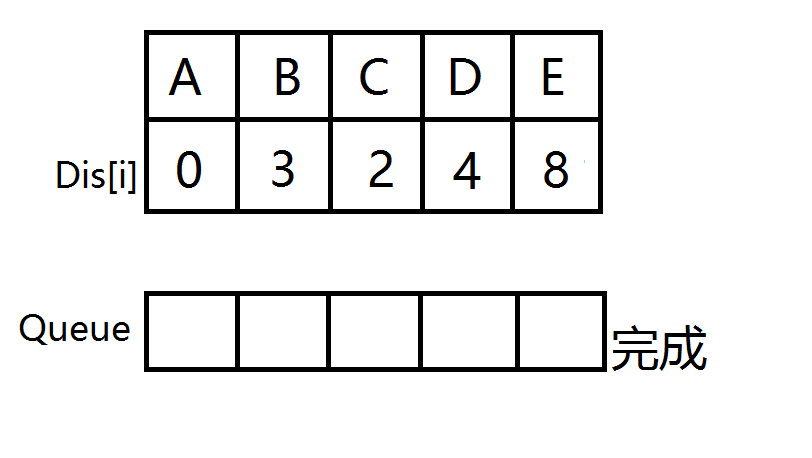
• 给定一个有向图，如下，求A~E的最短路。

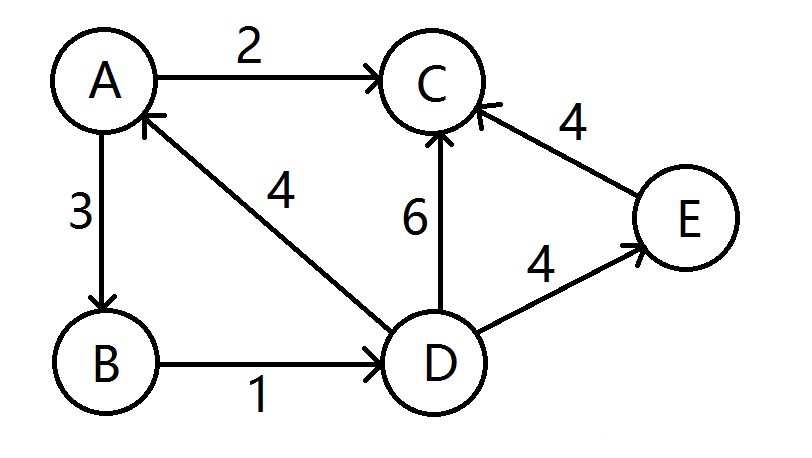
• 源点A首先入队，然后A出队，计算出到BC的距离会变短，更新距离数组，BC没在队列中，BC入队

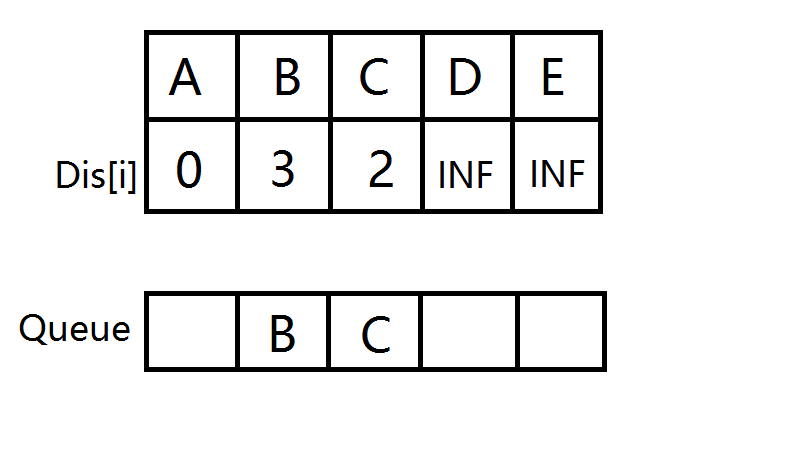
• B出队，计算出到D的距离变短，更新距离数组，D没在队列中，D入队。然后C出队，无点可更新。

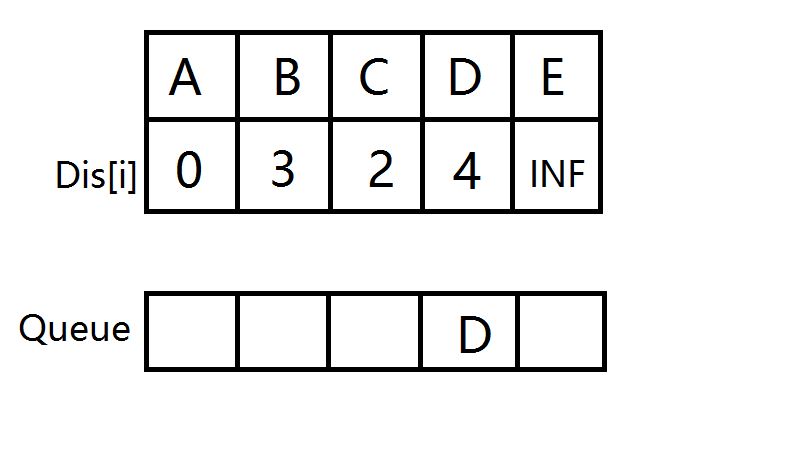
• D出队，计算出到E的距离变短，更新距离数组，E没在队列中，E入队。

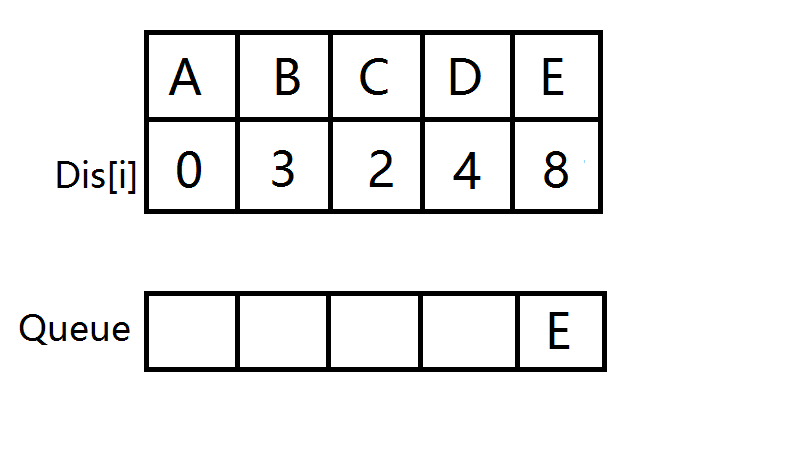
• E出队，此时队列为空，源点到所有点的最短路已被找到，A->E的最短路即为8

代码+注释

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 100010;
int h[N], e[N], w[N], ne[N], idx;//邻接表，存储图
int st[N];//标记顶点是不是在队列中
int dist[N];//保存最短路径的值
int q[N], hh, tt = -1;//队列

void add(int a, int b, int c){//图中添加边和边的端点
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void spfa(){
    q[++tt] = 1;//从1号顶点开始松弛，1号顶点入队
    dist[1] = 0;//1号到1号的距离为 0
    st[1] = 1;//1号顶点在队列中
    while(tt >= hh){//不断进行松弛
        int a = q[hh++];//取对头记作a，进行松弛
        st[a] = 0;//取完队头后，a不在队列中了
        for(int i = h[a]; i != -1; i = ne[i])//遍历所有和a相连的点
        {
            int b = e[i], c = w[i];//获得和a相连的点和边
            if(dist[b] > dist[a] + c){//如果可以距离变得更短，则更新距离

                dist[b] = dist[a] + c;//更新距离

                if(!st[b]){//如果没在队列中
                    q[++tt] = b;//入队
                    st[b] = 1;//打标记
                }
            }
        }
    }
}
int main(){
    memset(h, -1, sizeof h);//初始化邻接表
    memset(dist, 0x3f, sizeof dist);//初始化距离
    int n, m;//保存点的数量和边的数量
    cin >> n >> m;
    for(int i = 0; i < m; i++){//读入每条边和边的端点
        int a, b, w;
        cin >> a >> b >> w;
        add(a, b, w);//加入到邻接表
    }
    spfa();
    if(dist[n] == 0x3f3f3f3f )//如果到n点的距离是无穷，则不能到达 
        cout << "impossible";
    else cout << dist[n];//否则能到达，输出距离
    return 0;
}