题目描述
给定两个字符串A和B，现在要将A经过若干操作变为B，可进行的操作有：
删除–将字符串A中的某个字符删除。
插入–在字符串A的某个位置插入某个字符。
替换–将字符串A中的某个字符替换为另一个字符。
现在请你求出，将A变为B至少需要进行多少次操作。
样例
输入格式
第一行包含整数n，表示字符串A的长度。
第二行包含一个长度为n的字符串A。
第三行包含整数m，表示字符串B的长度。
第四行包含一个长度为m的字符串B。
字符串中均只包含大写字母。
输出格式
输出一个整数，表示最少操作次数。
数据范围
1≤n,m≤1000
输入样例：
10
AGTCTGACGC
11
AGTAAGTAGGC
输出样例：
4
算法1
(暴力枚举) $O(n^2)$
首先闫式dp镇楼
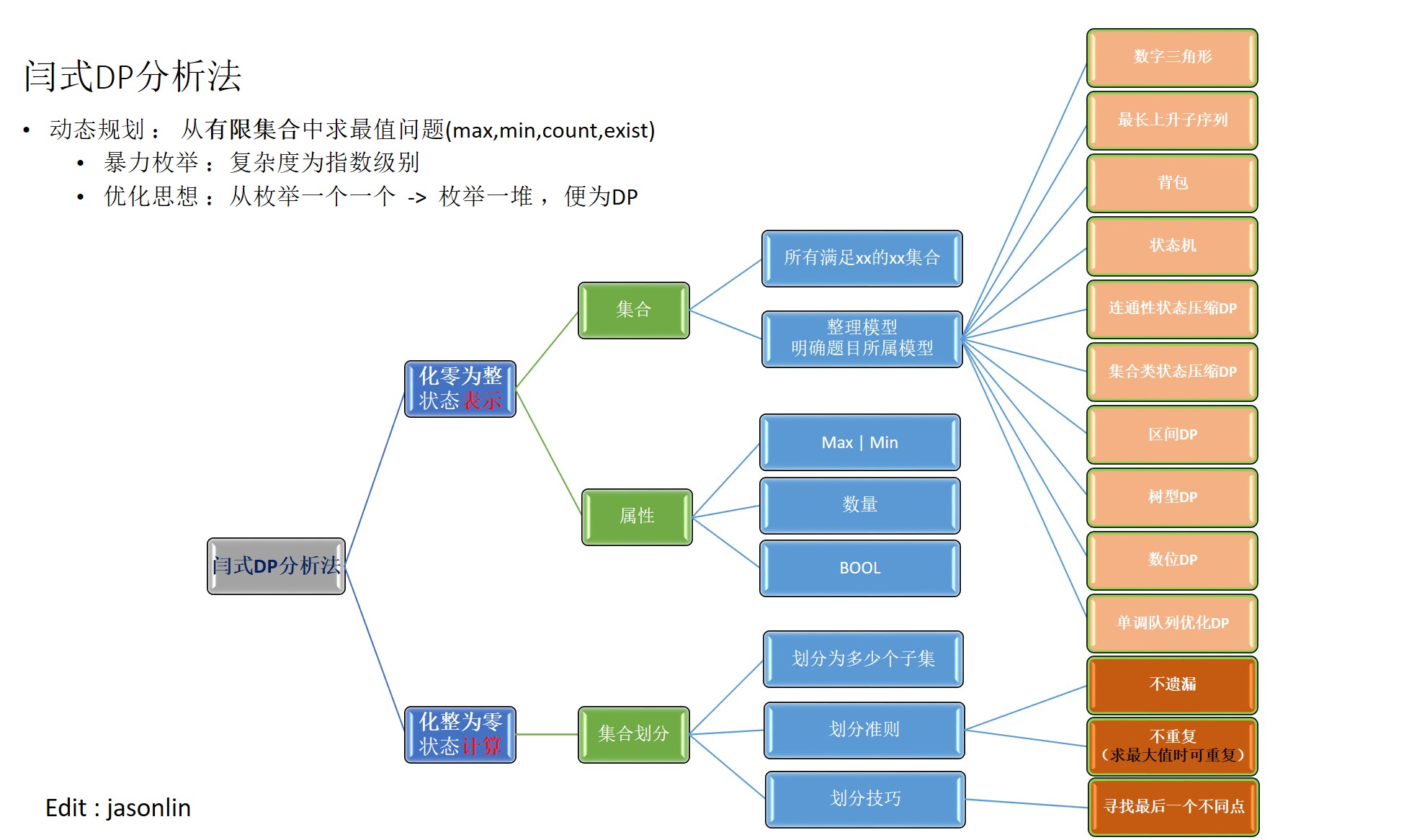
- 状态表示
dp[i][j]- 集合 ： 所有吧
a中的前i个字母变成b中前j个字母的集合的操作集合 - 属性 ： 所有操作中
操作次数最少的方案的操作数
- 集合 ： 所有吧
- 状态计算
状态划分 以对a中的第i个字母操作不同划分- 在该字母之后添加
- 添加一个字母之后变得相同，说明没有添加前
a的前i个已经和b的前j-1个已经相同 - 即 ：
dp[i][j] = dp[i][j-1] + 1
- 添加一个字母之后变得相同，说明没有添加前
- 删除该字母
- 删除该字母之后变得相同，说明没有删除前
a中前i-1已经和b的前j个已经相同 - 即 ：
dp[i][j] = dp[i-1][j] + 1
- 删除该字母之后变得相同，说明没有删除前
- 替换该字母
- 替换说明对应结尾字母不同，则看倒数第二个
- 即：
dp[i][j] = dp[i-1][j-1] + 1
- 啥也不做
- 对应结尾字母相同，直接比较倒数第二个
- 即：
dp[i][j] = dp[i-1][j-1]
- 在该字母之后添加
C++ 代码
#include <iostream>
#include <string>
#include <vector>
using namespace std;
int leastEdit(string a, string b){
int m = a.size(), n = b.size();
vector<vector<int>> dp(m+1, vector<int>(n+1));
for(int i = 0; i <= m; i++) dp[i][0] = i;
for(int i = 0; i <= n; i++) dp[0][i] = i;
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
dp[i][j] = min(dp[i][j - 1], dp[i - 1][j]) + 1; // 添加 和 删除
dp[i][j] = min(dp[i][j], dp[i-1][j-1] + (a[i - 1] != b[j - 1])); // 替换和 啥也不做
}
}
return dp[m][n];
}
int main(){
int a, b;
string s1, s2;
cin >> a >> s1 >> b >> s2;
cout << leastEdit(s1, s2);
return 0;
}
yxc 解法
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int m, n;
char a[N],b[N];
int dp[N][N];
int main()
{
scanf("%d%s", &m, a + 1); // a + 1 这里的小技巧
scanf("%d%s", &n, b + 1);
cout << a[1] << endl;
for(int i = 0; i <= m; i++) dp[i][0] = i; //全删除
for(int i = 0; i <= n; i++) dp[0][i] = i; //全插入
for(int i = 1; i <=m; i++)
for(int j = 1; j <=n; j++)
{
dp[i][j] = min(dp[i][j-1], dp[i-1][j]) + 1;
dp[i][j] = min(dp[i][j], dp[i-1][j-1] + (a[i] != b[j])); // 注意这里 i的原因 是 scanf("%d%s", &m, a + 1);
}
printf("%d\n",dp[m][n]);
return 0;
}
我帮作者注释一下，帮助大家理解
为什么要这样
第一个循环是a的前i个字母要和b的第0个字母进行比较，所以只能进行删除操作。
第二个循环是a的第0个字母要和b的前i个字母进行比较，所以只能进行增加也就是插入操作。
嘻嘻，明白了啦
插入操作的循环次数是m吧。
虽然但是，你写错了，应该一个是n一个是m
八达鸟，太漂亮了，手法啊，我一直强调手法啊，这手法多优美啊！
哈哈哈哈～～～
我不知道大家有没有像我一样有想复杂的可能
其一: 状态划分 以对a中的第i个字母操作不同划分,但是操作只能进行一次吗?
其二:对第i个位置的字母操作,那么如果i前面的位置进行过删除和添加操作,会不会对于定义的i指定的下标位置进行改变?
我认为 集合最严谨的定义方法 应该是 原先a字符串中第i位置所对应的字符元素的最后一步操作是什么?
而 重要的前提条件是,
任意 位置的元素进行的操作 的先后顺序不会影响该操作集的次数, 因为第i个位置的元素的删改添加()操作放在第一步 或者放在最后一步(第i个位置可能同时有进行删改添加操作,但是总会有一个最后的操作)都不会影响 a变成b的操作次数,所以我们都把第i位置的操作放在最后一步 ,然后对最后一步进行集合划分请问写成一句为啥过不了呢？
因为如果a[i]==b[j]的话就不用操作，即操作数加0，但你这样写操作数是加1了。在
法.......大法好
要和吴签做朋友吗2333
我只想说，那个图我直接看湿了，谢谢
hhh谢谢大湿夫～
？
虽然写的是dp但感觉可以用递归更容易理解，本质是一样的
以删除为例，最后一步是删除，前面需要的步数就是a的前i-1变成b的前j，也就是f[i-1][j]
思路清晰，tql
题目并没有规定第i位置的数字只能进行一次操作,这样的子集划分定义是有缺严谨性的
dp[i][j] = min(dp[i][j-1], dp[i-1][j]) + 1; 加一是为什么？？？
这里时增加和删除的操作，比较哪一种更小，只是一种操作，所以要加1，加在外面和里面不影响答案
y总用什么软件画的图啊，求推荐！！！
还可以这样吗？
大佬们， +(a[i]!=b[i]) 是什么意思？？？
bool 判断 -》a[i]!=b[i] == +1 a[i] == b[i] == +0;
大佬们，为什么插入和删除操作不用判断呢
当遍历到(i,j)的时候,说明a的前(i - 1) 已经和b的前(j - 1)相等了,所以这里只需要判断a[i]与b[j]的关系即可
想问一下a+1,b+1为什么要加1啊
应该是字符串下标从1开始
这样也过不了
是a[i] != b[j]
呜呜呜，大佬tql
添加和删除为什么不用判断a[i]==b[j-1]呢？
考虑集合的定义，前面的若干操作里已经让a[i] == b[j - 1]。
### 达瓦里希，我发现宝藏啦