算法提高课汇总

破环成链

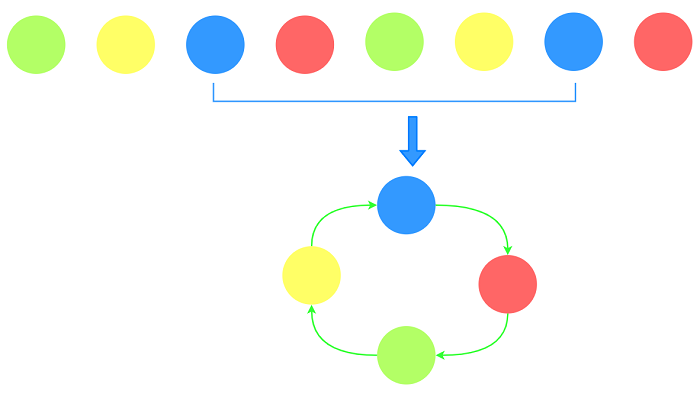
题目为环形问题, 可以通过2倍单链条达到与环路相同效果.

单调队列

从第$i$站顺时针出发能到达$i + 1$站, 则表明$p_i - d_i\ge 0$, 即到达$i + 1$站时汽油有剩余或者
恰好用完. 我们用$s_i = p_i - d_i$, 并计算$s_i$前缀和, 则$p_i - d_i = s_{i} - s_{i - 1}$ -->
则$s_j - s_{i-1}$表示: 从第$i$站出发到达$j + 1$站的剩余油量.

由于前缀和顺序从左至右(顺时针), 需要对顺时针和逆时针分别讨论.

顺时针方向

题目要求从起点$i$出发能够成功回到$i$(破环成链后对应下标$i + n$) — 由于$s_j - s_{i - 1}$表示从
$i$出发到达$j + 1$站剩余油量, 我们需要判断从$i$出发到达$i + 1\sim i + n$站是否满足条件, 则对应
$j$的范围为$i\sim i + n - 1$, 满足$s_j - s_{i - 1}\ge 0$. 我们只需考虑在长度为$n$的窗口内$s_j$
的最小值是否满足条件即可 — 单调队列实现.

逆时针方向

为方便考虑, 计算后缀和: $s_i = \sum_{j = i+1}^{2n} s_j$.

此时$s_i - s_{i+1}$表示从$i$站到达$i-1$站的剩余油量. 若从$i$出发逆时针能够成功回到$i$(对应下标$i - n$),
即满足$s_j - s_{i + 1}\ge 0$, $i - n + 1\le j\le i$, 我们只需考虑最小的$s_j$是否满足条件.

具体实现

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e6 + 10;

int n;
int p[N], d[N], q[N * 2];
ll  s[N * 2];
bool st[N]; //st[i] = true: 从i出发可以成功周游一圈

int main()
{
    scanf("%d", &n);
    for ( int i = 1; i <= n; i ++ ) scanf("%d%d", &p[i], &d[i]);

    //顺时针
    //pi - di的前缀和
    for ( int i = 1; i <= n; i ++ ) s[i] = s[i + n] = p[i] - d[i];
    for ( int i = 1; i <= n * 2; i ++ ) s[i] += s[i - 1];

    //单调队列
    int hh = 0, tt = -1; //q[++ tt] = 2 * n + 1
    for ( int i = 2 * n; i; i -- )
    {
        if ( hh <= tt && q[hh] > i + n - 1 )    hh ++; //超出[i, i + n - 1]
        while ( hh <= tt && s[q[tt]] >= s[i] )  tt --;
        q[++ tt] = i;

        //从i顺时针出发的过程中油量不会小于0
        if ( i <= n && s[q[hh]] - s[i - 1] >= 0 )   st[i] = true;
    }

    //逆时针
    //pi - d(i - 1)的后缀和
    d[0] = d[n]; 
    for ( int i = 1; i <= n; i ++ ) s[i] = s[i + n] = p[i] - d[i - 1];
    for ( int i = 2 * n; i; i --  ) s[i] += s[i + 1];

    //单调队列
    hh = 0, tt = -1; //q[++ tt] = 0
    for ( int i = 1; i <= 2 * n; i ++ )
    {
        if ( hh <= tt && q[hh] < i - n + 1 )   hh ++;    //超出[i - n + 1, i]
        while ( hh <= tt && s[q[tt]] >= s[i] )  tt --;
        q[++ tt] = i;
        if ( i > n && s[q[hh]] - s[i + 1] >= 0 )    st[i - n] = true;
    }

    for ( int i = 1; i <= n; i ++ )
        puts( st[i] ? "TAK" : "NIE" );

    return 0;
}