前置知识

• 假设 $x$ 能唯一分解为 ${p_1}^{e_1}{p_2}^{e_2}\ldots{p_k}^{e_k}$，莫比乌斯函数 $\mu(x)$ 定义为：

$$\mu(x) = \begin{cases} \begin{aligned} 0\qquad &,\exists e_i > 1 \\\ 1\qquad &,k \text{是偶数} \\\ -1\qquad &,k \text{是奇数} \end{aligned} \end{cases} \quad \text{或} \quad \mu(x) = \begin{cases} \begin{aligned} 1\qquad &,n = 1 \\\ (-1)^k \qquad &,n = p_1 p_2 \ldots p_k \\\ 0\qquad &,\text{其他} \end{aligned} \end{cases}$$

题目分析

给定 $a, b, d$，求满足 $1\leq x\leq a, 1\leq y\leq b$，并且 $\gcd(x, y) = d$ 的数对 $(x, y)$ 个数 等价于 求满足 $1\leq x’\leq \lfloor \dfrac{a}{d} \rfloor$，$1\leq y’\leq \lfloor \dfrac{b}{d} \rfloor$，并且 $\gcd(x’, y’) = 1$ 的数对 $(x’, y’)$ 个数，即求两个区间内有多少对这样的数对是互质的。

证明：假设 $\gcd(\dfrac{x}{d}, \dfrac{y}{d}) > 1$，那么 $\gcd(x, y) > d$，矛盾。

可以用容斥原理求解，设 $\lfloor \dfrac{a}{d} \rfloor = a’$，$\lfloor \dfrac{b}{d} \rfloor = b’$ ，接下来统计不合法的对数：

有一个质公因子的方案数量：

$$\lfloor\dfrac{a’}{2}\rfloor \cdot \lfloor \dfrac{b’}{2} \rfloor + \lfloor\dfrac{a’}{3}\rfloor \cdot \lfloor \dfrac{b’}{3} \rfloor + \lfloor\dfrac{a’}{5}\rfloor \cdot \lfloor \dfrac{b’}{5} \rfloor + \cdots$$

有两个质公因子的方案数量：

$$\lfloor\dfrac{a’}{2\times 3}\rfloor \cdot \lfloor \dfrac{b’}{2\times 3} \rfloor + \lfloor\dfrac{a’}{2\times 5}\rfloor \cdot \lfloor \dfrac{b’}{2\times 5} \rfloor + \cdots$$

有三个质公因子的方案数量：

$$\lfloor\dfrac{a’}{2\times 3\times 5}\rfloor \cdot\lfloor\dfrac{b’}{2\times 3\times 5}\rfloor + \cdots$$

所以根据容斥原理，合法方案数为：

$$\begin{split} ans &= a’b - \lfloor\dfrac{a’}{2}\rfloor \cdot \lfloor\dfrac{b’}{2}\rfloor - \lfloor\dfrac{a’}{3}\rfloor \cdot \lfloor\dfrac{b’}{3}\rfloor - \cdots \qquad \text{(只含一个质公因子)} \\\ &+ \lfloor\dfrac{a’}{2\times 3}\rfloor \cdot \lfloor\dfrac{b’}{2\times 3}\rfloor + \cdots \qquad \text{(只含两个质公因子)} \\\ &- \lfloor\dfrac{a’}{2\times 3\times 5}\rfloor \cdot \lfloor\dfrac{b’}{2\times 3\times 5}\rfloor - \cdots \qquad \text{(只含三个质公因子)} \\\ \end{split}$$

注意到符号项就是莫比乌斯函数，故合法方案数可用莫比乌斯函数表示：

$$ans = a’b’ + \sum\limits_{i=2}^{\min \lbrace a’, b’\rbrace} \lfloor \dfrac{a’}{i} \rfloor \cdot \lfloor \dfrac{b’}{i} \rfloor\cdot \text{mobius}[i]$$

注意，$1\sim x$ 中因子 $d$ 的个数就是 $\lfloor \dfrac{x}{d} \rfloor$ 个，不仅只有质因子有这样的性质

如果直接枚举 $i$，由于 $a’, b’\leq 5\times 10^4$，复杂度是 $O(n)$ 级别，并且询问个数有 $10^5$，直接枚举是 $O(n^2)$ 级别，考虑优化。

我们发现，这个式子理论上 $i$ 最多需要枚举 $N$ 次，但实际上因为整除的缘故，有很多 $i$ 对应的 $\lfloor \dfrac{a’}{i} \rfloor$ 和 $\lfloor \dfrac{b’}{i} \rfloor$ 都是相同的，所以是冗余枚举。由于 $i$ 从小到大枚举，$\lfloor \dfrac{a’}{i} \rfloor$ 都是单调递减的，并且理论上只有 $2\sqrt {a}$ 个不同的值（$\lfloor \dfrac{b’}{i} \rfloor$ 同样）。这里用到了 AcWing 199. 余数之和 中的知识。

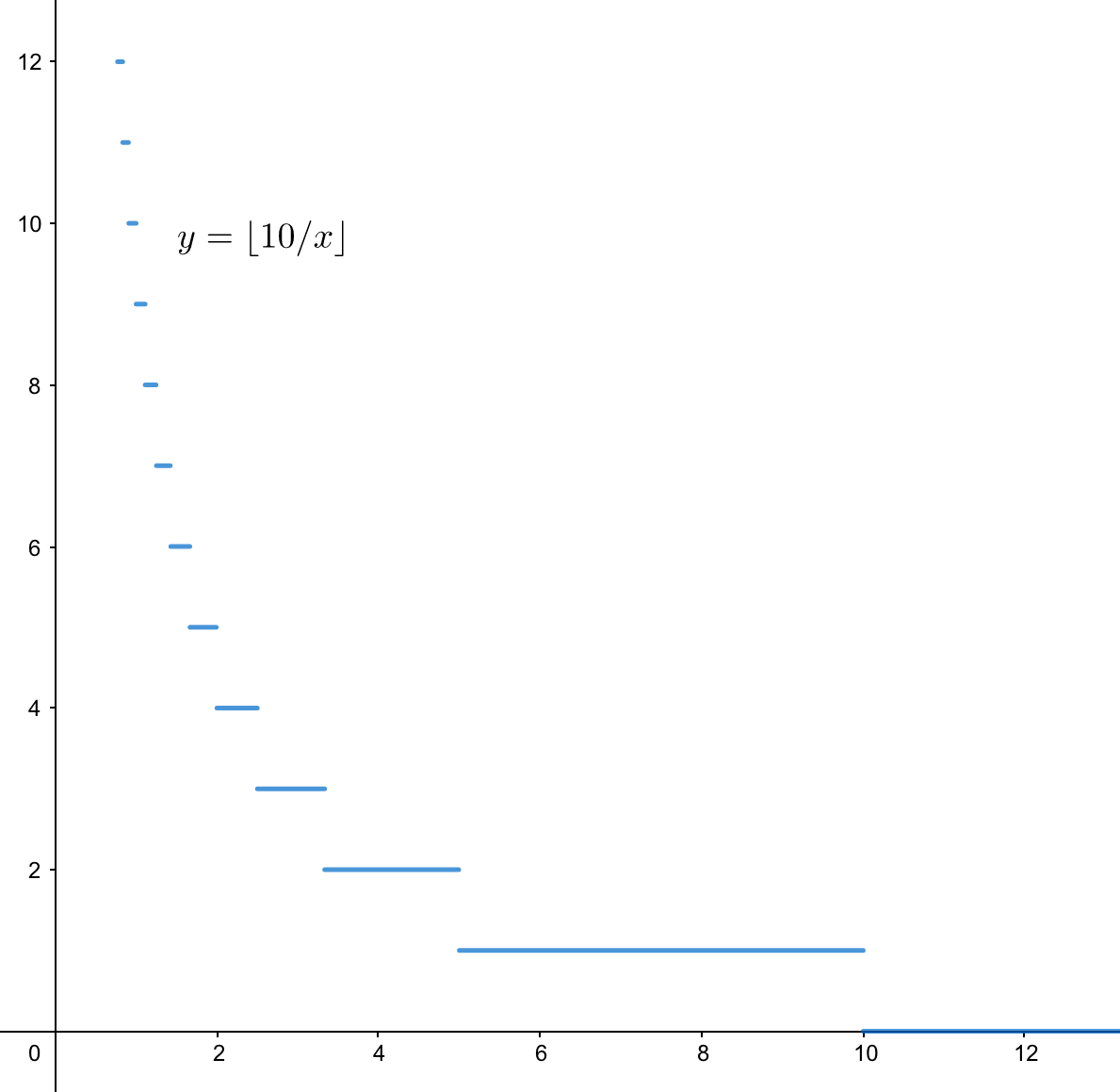
分块证明：

分段讨论：

• 当 $i\leq \sqrt k$ 时，因为 $i$ 是 $[1, \sqrt k]$ 中的整数，所以只有 $\sqrt k$ 个不同的 $\lfloor \dfrac{k}{i} \rfloor$ 值。
• 当 $i > k$ 时，$\lfloor \dfrac{k}{i} \rfloor \leq \sqrt{k}$，又因为式子取整了，所以式子只能取到 $[1, \sqrt k]$ 的值，故最多也只有 $\sqrt k$ 个不同的 $\lfloor \dfrac{k}{i} \rfloor$ 值。

有关当 $i > k$ 时，$\lfloor \dfrac{k}{i} \rfloor \leq \sqrt k$ 的证明：

由于下取整，所以 $\lfloor \dfrac{k}{i} \rfloor \leq k$，假设 $\lfloor \dfrac{k}{i} \rfloor > \sqrt k$，那么 $\lfloor \dfrac{k}{i} \rfloor \cdot \sqrt{k} > \sqrt{k}^2 = k$，矛盾。

图和证明引自：墨染空

我们现在已经证明出了，可以将一段 长度为 $n$ 的序列分成 $2\sqrt n$ 段的序列，如果我们能做到 $O(1)$ 处理每一段，那么就可以将原先 $O(n^2)$ 的复杂度优化至 $O(n\sqrt n)$。

假设有 $\lfloor \dfrac{a}{x} \rfloor$，假设此时的 $x$ 是下界，求能使这个值不变的，最大的 $x$ 为多少（上界），记这个上界是 $g(x)$。举个例子，$\lfloor \dfrac{24}{9} \rfloor$，值为 $2$，其中 $9$ 是下界，那么上界就是 $12$，因为 $\lfloor \dfrac{24}{13} \rfloor = 1$。所以有 $\lfloor \dfrac{a}{x} \rfloor = \lfloor \dfrac{a}{g(x)} \rfloor$，且 $\lfloor \dfrac{a}{g(x)} \rfloor > \lfloor \dfrac{a}{g(x)+1} \rfloor$。这里的 $g(x)$ 实际上是有公式的：

$$g(x) = \lfloor \dfrac{a}{\lfloor \frac{a}{x} \rfloor} \rfloor$$

$g(x)$ 公式证明：

我们要证明的是 $\lfloor \dfrac{a}{g(x)} \rfloor = \lfloor \dfrac{a}{x} \rfloor$，且 $\lfloor \dfrac{a}{x} \rfloor > \lfloor \dfrac{a}{g(x) + 1} \rfloor$，只有满足这个条件，才能证明 $g(x)$ 是使这个值不变的上界。

由于：

$$g(x) = \lfloor \dfrac{a}{\lfloor \frac{a}{x} \rfloor} \rfloor \geq \lfloor \dfrac{a}{\frac{a}{x}} \rfloor = \lfloor x \rfloor = x \quad (x\in \mathbb{Z})$$

故 $g(x)\geq x$，所以 $\lfloor \dfrac{a}{g(x)} \rfloor \leq \lfloor \dfrac{a}{x} \rfloor$。又因为

$$\lfloor \dfrac{a}{\lfloor \frac{a}{\lfloor \frac{a}{x} \rfloor} \rfloor} \rfloor\geq \lfloor \dfrac{a}{\frac{a}{\lfloor \frac{a}{x} \rfloor}} \rfloor = \lfloor \dfrac{a}{x} \rfloor$$

所以 $\lfloor \dfrac{a}{g(x)} \rfloor \geq \lfloor \dfrac{a}{x} \rfloor$，第一部分证毕。

用带余除法证明第二部分：

设 $a = kx + r$， 则 $0\leq r < x$，并且用第一部分证得的结论，代入第二部分式子得：

$$\lfloor \dfrac{a}{x} \rfloor = k,\quad \lfloor \dfrac{a}{g(x) + 1} \rfloor = \lfloor \dfrac{a}{\lfloor \frac{a}{k} \rfloor + 1} \rfloor$$

所以等价于证明

$$k > \lfloor \dfrac{a}{\lfloor \frac{a}{k} \rfloor + 1} \rfloor \iff \lfloor k \rfloor > \lfloor \dfrac{a}{\lfloor \frac{a}{k} \rfloor + 1} \rfloor,\quad k\in \mathbb{Z}$$

等价于证明

$$k(\lfloor \dfrac{a}{k} \rfloor + 1) > a$$

再令 $a = pk + q$，则 $0\leq q < k$，等价于证明：

$$\begin{aligned} k(p + 1) &> pk + q \\\ kp + k &> pk + q \\\ k &> q \end{aligned}$$

由于 $0\leq q < k$，因此得证。

完整代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;
const int N = 50010;

int primes[N], cnt;
bool st[N];
int mobius[N], sum[N];

void init(int n) {
    mobius[1] = 1;  // 莫比乌斯函数特判
    for (int i = 2; i <= n; i ++ ) {
        if (!st[i]) {
            primes[cnt ++ ] = i;
            mobius[i] = -1;
        }
        for (int j = 0; primes[j] <= n / i; j ++ ) {
            int t = primes[j] * i;
            st[t] = true;
            if (i % primes[j] == 0) {
                mobius[t] = 0;
                break;
            }
            // 这里还是有点绕的
            // 根据线性筛的知识，pj 一定是 t = pj * i 的最小质因子
            // 这里由于没有 break，说明 pj 小于 i 的所有质因子，也就不是i的质因子
            // 说明 t = pj * i，t 多了一个新的不同质因子，就乘上一个-1就行了
            mobius[t] = mobius[i] * -1;  
        }
    }
    for (int i = 1; i <= n; i ++ ) sum[i] = sum[i - 1] + mobius[i];  // 维护u(x)前缀和
}

int main() {
    init(N - 1);
    int T;
    scanf("%d", &T);
    while (T -- ) {
        int a, b, d;
        scanf("%d%d%d", &a, &b, &d);

        a /= d, b /= d;  // a', b'

        // n为 min(a', b')
        int n = min(a, b);

        LL res = 0;

        // l r, 是每一段的左右边界
        // 每次只能取较小的那个上界作为这一段的右端点r
        // 然后下次迭代时下一段的左端点就是r + 1
        for (int l = 1, r; l <= n; l = r + 1) {
            r = min(n, min(a / (a / l), b / (b / l)));
            res += (sum[r] - sum[l - 1]) * (LL)(a / l) * (b / l);
        }
        printf("%lld\n", res);
    }
    return 0;
}