题目描述

给你一个 m x n 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是：

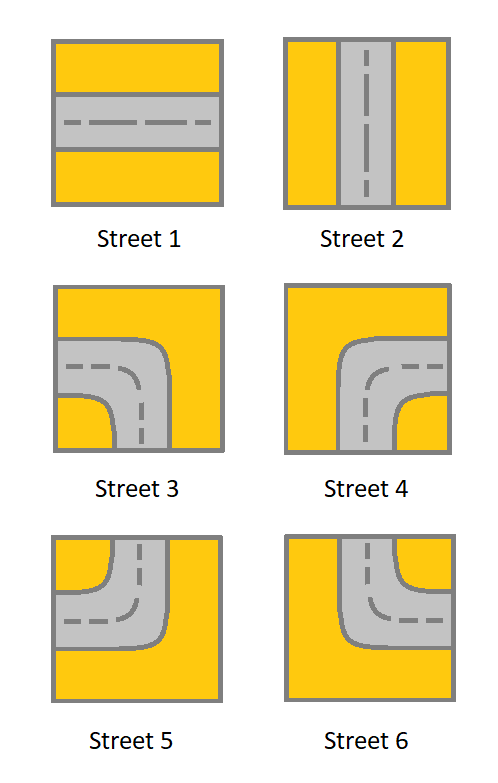
1 表示连接左单元格和右单元格的街道。
2 表示连接上单元格和下单元格的街道。
3 表示连接左单元格和下单元格的街道。
4 表示连接右单元格和下单元格的街道。
5 表示连接左单元格和上单元格的街道。
6 表示连接右单元格和上单元格的街道。

你最开始从左上角的单元格 (0,0) 开始出发，网格中的「有效路径」是指从左上方的单元格 (0,0) 开始、一直到右下方的 (m-1,n-1) 结束的路径。该路径必须只沿着街道走。

注意：你 不能 变更街道。

如果网格中存在有效的路径，则返回 true，否则返回 false 。

样例

示例 1：
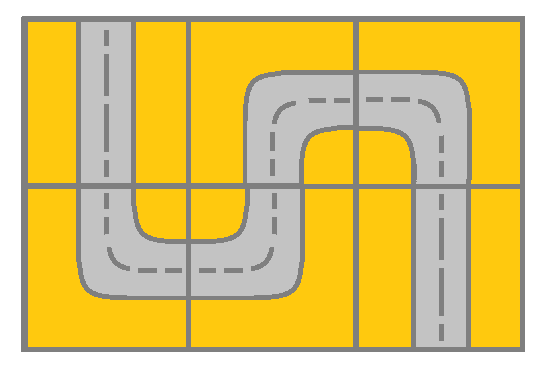
输入：grid = [[2,4,3],[6,5,2]]
输出：true
解释：如图所示，你可以从 (0, 0) 开始，访问网格中的所有单元格并到达 (m - 1, n - 1) 。

示例 2：
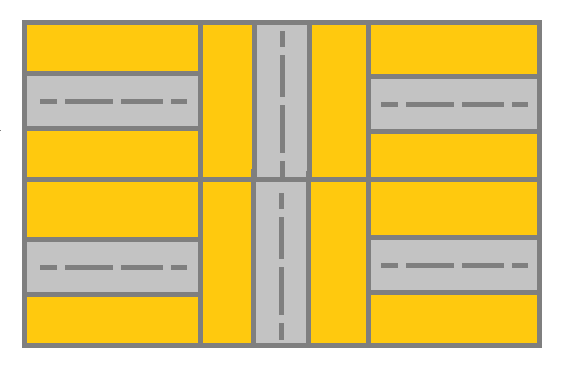
输入：grid = [[1,2,1],[1,2,1]]
输出：false
解释：如图所示，单元格 (0, 0) 上的街道没有与任何其他单元格上的街道相连，你只会停在 (0, 0) 处。

示例 3：
输入：grid = [[1,1,2]]
输出：false
解释：你会停在 (0, 1)，而且无法到达 (0, 2) 。
示例 4：

输入：grid = [[1,1,1,1,1,1,3]]
输出：true
示例 5：

输入：grid = [[2],[2],[2],[2],[2],[2],[6]]
输出：true
 

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 300
1 <= grid[i][j] <= 6

算法 dfs

时间复杂度 $O(nm)$

这个题目本质上是dfs求连通性的问题，难点在当前的街道是否可以向他所表示的两个方向前进
如果可以的话就继续递归到下一个未访问过的点，如果存在到达终点的路径返回true,否则返回false

规定方向：上->0,右->1,下->2,左->3 dx[] = {-1,0,1,0},dy = {0,1,0,-1}
在用一个数组存储每个街道可以走的方向 dir[][2] = {{},{1,3},{0,2},{2,3},{1,2},{0,3},{0,1}}

C++ 代码

int dx[] = {-1,0,1,0}, dy[] = {0,1,0,-1} ;
int dir[][2] = {{},{1,3},{0,2},{2,3},{1,2},{0,3},{0,1}} ;
bool vis[310][310] = {false};
class Solution {
public:

    bool check(int d,int g){
        int one = (dir[g][0] + 2) % 4 ;//将方向取个反向，便于判断,上和下对应，左和右对应
        int two = (dir[g][1] + 2) % 4 ;
        if(d == one || d == two) return true ;
        return false ;
    }

    bool dfs(int x,int y,vector<vector<int>>& grid,int n,int m){
        vis[x][y] = true ;
        if(x == n-1 && y == m-1) return true ;
        int gid = grid[x][y] ;
        for(int i=0;i<2;i++){
            int dd = dir[gid][i] ;
            int a = x + dx[dd], b = y + dy[dd] ;
            if(a<0 || a>=n || b<0 || b>=m) continue ;  //判断是否出界
            if(vis[a][b]) continue ; //防止走回头路
            if(!check(dd,grid[a][b])) continue ;  //判断当前街道的这个方向是否可以扩展到下一个街道
            if(dfs(a,b,grid,n,m)) return true ;  //如果存在一条到从终点的路径的话，放回true
        }
        return false ;
    }

    bool hasValidPath(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size() ;
        memset(vis,false,sizeof vis) ;//lc调用的是函数，所以每次要把判重数组清空
        bool ans = dfs(0,0,grid,n,m) ;

        return ans ;
    }
};