AcWing 848. 拓扑排序--思路介绍+图解模拟+详细代码注释

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 848. 拓扑排序--思路介绍+图解模拟+详细代码注释原题链接简单

作者：

Hasity , 2022-03-24 00:41:39 , 所有人可见 , 阅读 19202

1142

142

$\color{green}{<–画图不易，点下这里赞一下吧}$

啥是拓扑排序?

一个有向图，如果图中有入度为 0 的点，就把这个点删掉，同时也删掉这个点所连的边。
一直进行上面出处理，如果所有点都能被删掉，则这个图可以进行拓扑排序。

举例子

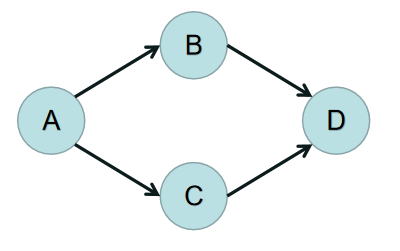
开始时，图是这样的状态，发现A的入度为 0，所以删除A和A上所连的边，结果如下图：

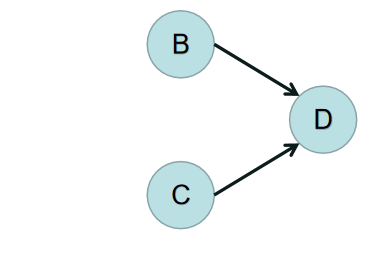
这时发现B的入度为 0，C的入度为 0，所以删除B和B上所连的边、C和C上所连的边，结果如下图：

这时发现发现D的入度为 0，所以删除D和D上所连的边(如果有就删)，结果如下图：

这时整个图被删除干净，所有能进行拓扑排序。

解题思路

首先记录各个点的入度
然后将入度为 0 的点放入队列
将队列里的点依次出队列，然后找出所有出队列这个点发出的边，删除边，同事边的另一侧的点的入度 -1。
如果所有点都进过队列，则可以拓扑排序，输出所有顶点。否则输出-1，代表不可以进行拓扑排序。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int q[N], hh = 0, tt = -1;//队列保存入度为0的点，也就是能够输出的点，
int n, m;//保存图的点数和边数
int d[N];////保存各个点的入度

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void topsort(){
    for(int i = 1; i <= n; i++){//遍历一遍顶点的入度。
        if(d[i] == 0)//如果入度为 0, 则可以入队列
            q[++tt] = i;
    }
    while(tt >= hh){//循环处理队列中点的
        int a = q[hh++];
        for(int i = h[a]; i != -1; i = ne[i]){//循环删除 a 发出的边
            int b = e[i];//a 有一条边指向b
            d[b]--;//删除边后，b的入度减1
            if(d[b] == 0)//如果b的入度减为 0,则 b 可以输出，入队列
                q[++tt] = b;
        }
    }
    if(tt == n - 1){//如果队列中的点的个数与图中点的个数相同，则可以进行拓扑排序
        for(int i = 0; i < n; i++){//队列中保存了所有入度为0的点，依次输出
            cout << q[i] << " ";
        }
    }
    else//如果队列中的点的个数与图中点的个数不相同，则可以进行拓扑排序
        cout << -1;//输出-1，代表错误
}


int main(){
    cin >> n >> m;//保存点的个数和边的个数
    memset(h, -1, sizeof h);//初始化邻接矩阵
    while (m -- ){//依次读入边
        int a, b;
        cin >> a >> b;
        d[b]++;//顶点b的入度+1
        add(a, b);//添加到邻接矩阵
    }
    topsort();//进行拓扑排序
    return 0;
}

画图不易，求点赞~

79 评论

柏筱Bociao 2023-06-11 10:33

海绵宝宝永远单身！

CyberCheems 2023-01-17 23:40

看一遍就懂了，思路非常清晰，tql

初学者- 11个月前

用队列写的，但是感觉比用数组模拟难写一点

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;

const int N =100010;

int n,m;
int h[N],e[N],ne[N],idx;
queue<int> q,res;
int d[N],count;

void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void topsort()
{
    for(int i=1;i<=n;i++)
    {
        if(d[i]==0)
        {
            q.push(i);
        }
    }

    while(q.size())
    {
        int a=q.front();
        res.push(a);
        count++;
        q.pop();

        for(int i=h[a];i!=-1;i=ne[i])
        {
            int b=e[i];
            d[b]--;
            if(d[b]==0) q.push(b);
        }
    }

    if(count==n)
    {
        for(int i=0;i<n;i++)
        {
            cout<<res.front()<<' ';
            res.pop();
        }
    }
    else
    {
        cout<<-1;
    }
}

int main()
{
    cin>>n>>m;
    memset(h,-1,sizeof h);

    while(m--)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
        d[b]++;
    }
    topsort();
    return 0;
}

lostin 10个月前

stl队列效率很慢，最好不要用，数组模拟就好

en_red 1个月前 ·北京

用queue写的话，还得要一个res来储存每次被pop出去的队头

350206A_u10551154ser30142325 9天前 ·福建

我也是

350206A_u10551154ser30142325 9天前 ·福建回复了 350206A_u10551154ser30142325 的评论

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
int n,m,cnt,a[N],ver[N],nxt[N],head[N],deg[N],tot;
void add(int x,int y){
    ver[++tot]=y,nxt[tot]=head[x],head[x]=tot;
    deg[y]++;
}
void topsort(){
    queue<int>q;
    for(int i=1;i<=n;i++){
        if(deg[i]==0)q.push(i);
    }
    while(q.size()){
        int y=q.front();
        q.pop();
        a[++cnt]=y;
        for(int i=head[y];i;i=nxt[i]){
            int v=ver[i];
            if(--deg[v]==0)q.push(v);
        }
    }
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        add(x,y);
    }
    topsort();
    if(cnt==n){
        for(int i=1;i<=cnt;i++){
            cout<<a[i]<<" ";
        }
    }else cout << -1;
    return 0;
}

350206A_u10551154ser30142325 9天前 ·福建回复了 350206A_u10551154ser30142325 的评论

414ms

一一呀 9个月前

用stl的queue的写法：

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int d[N]; //每个点的入度
int n, m;

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
    d[b]++; //b的入度加1
}

void topsort()
{
    queue<int> q;
    vector<int> ans;
    for (int i = 1; i <= n; i++)
    {
        if (d[i] == 0) q.push(i); //入度为0节点的入列，可以作为拓扑序列的第一个
    }
    while (q.size())
    {
        int t = q.front();
        ans.push_back(t);
        q.pop();
        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i]; //节点的编号
            d[j]--; //删除出队的结点指向这个点的边，这个点的入度-1
            if (d[j] == 0)
            {
                q.push(j);
            }
        }
    }
    if (ans.size() == n) // 如果队列中的点的个数与图中点的个数相同，则可以进行拓扑排序
    {
        for (int i = 0; i < n; i++) printf("%d ", ans[i]);
    }
    else
    {
        printf("-1");
    }
}



int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    while (m--)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }
    topsort();
    return 0;
}

我看是个熊 2023-03-16 09:06

海绵宝宝yyds

风起于浮萍之末 2024-02-19 16:14

为什么不能用stl中的队列来做，queue不也可以存储元素吗

佩奇公主 2024-02-23 00:59

用的是数组模拟队列，出队元素是指针往后挪一个，但用queue就是直接出队了，用queue直接出队不好统计点数，因为点数如果小于n，要输出-1，等于的话输出序列

羡笙雨 2024-02-28 16:32

雀氏牛逼，我的老baby

Beeee 2024-01-17 01:35

海绵宝宝是我的神

风中孤独的一匹马 2023-12-12 22:23

%%%

云寄_9 2023-09-29 00:55

为啥遍历一遍顶点的入度的时候是1到n，但是输出的时候又是0到n-1啊

欧豆豆 2023-11-01 01:02

存储图结点的时候是点的编号是从1开始的，输出的时候是输出队列里的元素，队列中的是从0开始存储的。

天蓝Bluky 2023-04-04 21:48

提示：关于图的存储方法不明白的同学如果搜邻接表存储图搜不到想要的答案，搜一下“链式前向星”

梵天 2024-03-31 11:53

存储图为什么有些不用add函数，而是用的bool[N][N]，有什么区别呀

天蓝Bluky 2024-03-31 15:53 回复了梵天的评论

见算法基础课三（一）中关于图的存储的内容，使用add函数的方法对应的就是邻接表存储图，适用于稀疏图；用二维数组存储的方法对应的就是邻接矩阵存储图，适用于稠密图

酱香豆腐皮 2023-03-12 21:12

海绵宝宝Yydx

名为溶菌酶的溶酶菌 2023-02-04 23:37

有一个问题，初始化是链表的初始化，可是批注为什么是邻接矩阵呢

旧_忆 2023-04-15 12:12

应该是邻接表

会有时 2023-05-22 14:07 回复了旧_忆的评论

只是初始化头插链表的首节点为-1，h[a]存储的是a到最后插入节点的边，作为首节点，若为-1，则a没有出度边。而邻接表是整体的概念

acwing_83420 2023-09-27 00:04

你这个名字，不会是au的粉丝吧，hh

名为溶菌酶的溶酶菌 2023-10-09 08:30 回复了 acwing_83420 的评论

hh，被发现了

acwing_83420 2023-10-09 12:40 回复了名为溶菌酶的溶酶菌的评论

小桐努力变强 2022-10-02 17:13

respect

五九 8天前 ·河南

太强了！真的思路太清晰了吧！大佬orz

QL_8 8天前 ·贵州

这里不用考虑重边和自环吗

小灰象 8个月前

求问我的代码哪里有问题呀？编译通过但是输出总是不对

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
const int N = 100010;
int h[N], e[N*2], ne[N*2], idx;
bool st[N]; // 记录某个点是否已经搜索过
int n, ans = N;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}


int dfs(int u){
    st[u] = true;
    int sum = 0, size;

    for(int i = h[u]; i!=-1; i = ne[i]){
        int j = e[i];
        if(!st[j]){
            int s = dfs(j); // 返回j所在分支的所有节点数
            // sum是为了求删掉节点之下的所有节点数（这样就好求节点之上的节点数了，n-sum）
            sum += s; 
            size = max(size, s); // 看哪一个分支最大
        }

    }
    size = max(size, n-(sum+1));
    ans = min(size, ans);
    return sum+1;
}


int main(){
    scanf("%d", &n);
    memset(h, -1, sizeof(h));
    for(int i = 0; i<n-1; i++){
        int a,b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }

    dfs(1);
    cout << ans <<endl;
    return 0;
}