题目描述

给定一个自然数N，要求把N拆分成若干个正整数相加的形式，参与加法运算的数可以重复。

注意:

• 拆分方案不考虑顺序；
• 至少拆分成2个数的和。

求拆分的方案数 mod 2147483648的结果。

样例

输入样例：
7
输出样例：
14

算法

(DP,完全背包问题) $ O(nm) $

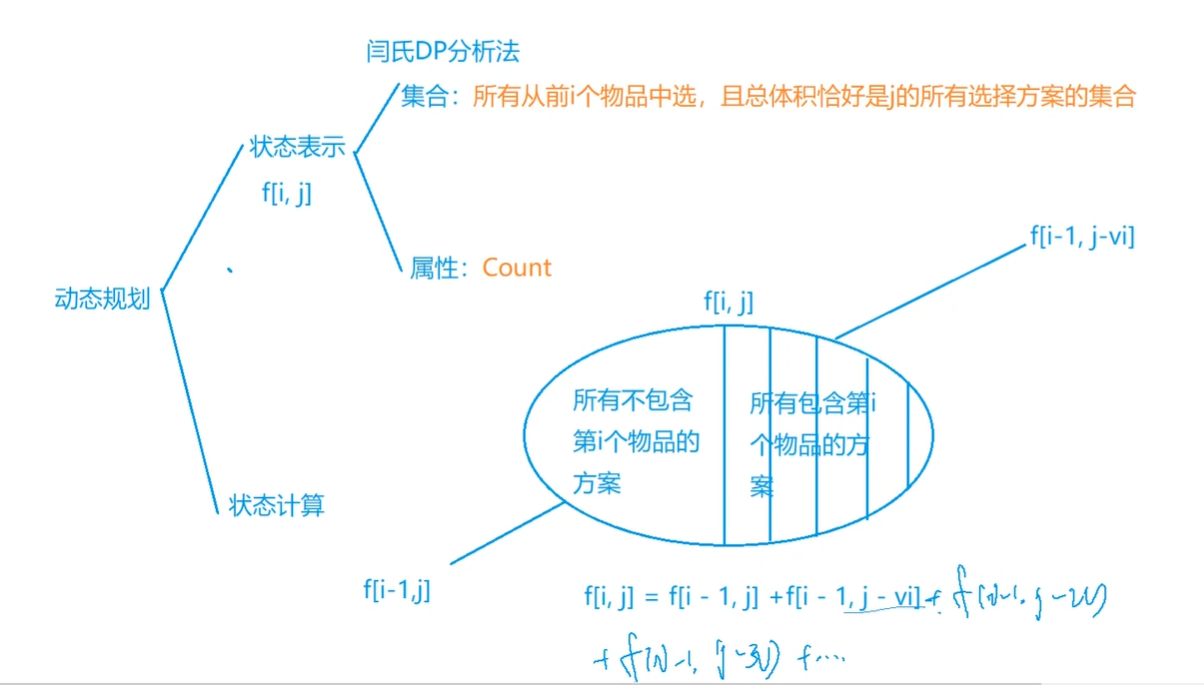
可以转化为完全背包问题求方案数：

• 将总和 N 看作背包容量；
• 将$1 \thicksim N$这$N$个自然数看作体积为$i(i=1,\dots,N)$的物品，每种物品都可以无限次使用；

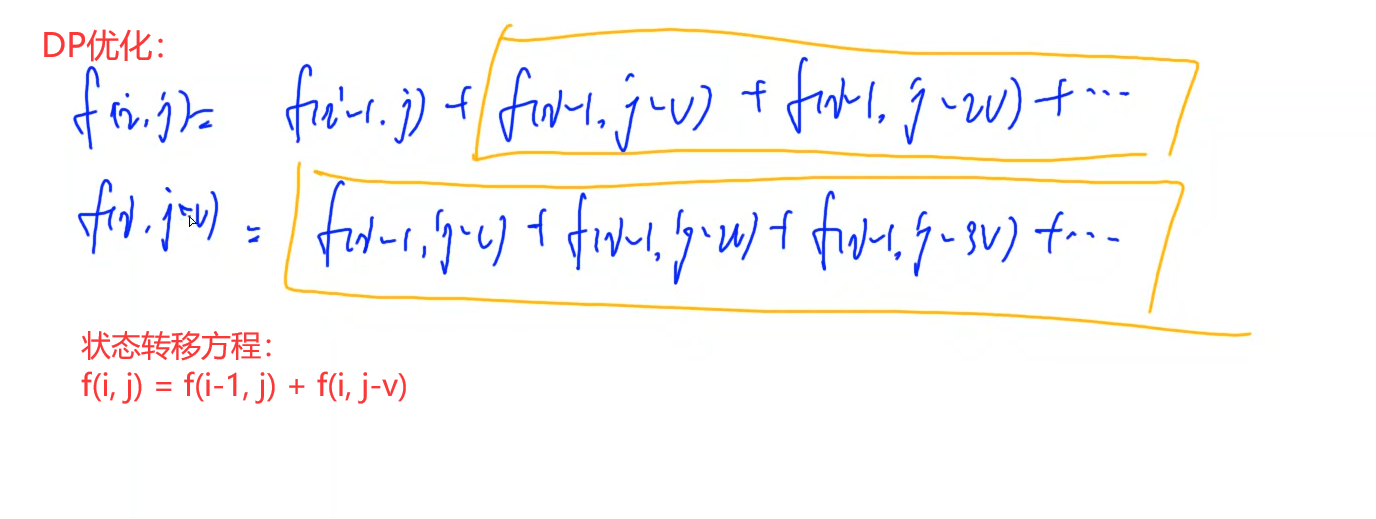
时间复杂度

背包问题的时间复杂度是 $O(nm)$。

C++ 代码

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 4010;
const LL MOD =  2147483648LL;  // 默认数字为int类型，因此数字后要加LL

int n;
LL f[N];  // 方案数

int main()
{
    cin >> n;
    f[0] = 1;  // 初始化：一个数字也没有且和为0的方案只有一种
    for(int i = 1; i <= n; i++)
        for(int j = i; j <= n; j++)
            f[j] = (f[j] + f[j-i]) % MOD;
    cout << f[n] - 1 << endl;  // 由于至少拆分成2个数的和，所以要减去1个数字组成的方案数
    return 0;
}